5.7A: \(\pi \)-Bonding in \(CO_2\)
- Page ID
- 2562
Molecular Orbital (MO) theory is used by scientists to understand bonding in molecules. Carbon dioxide is a linear, centrosymmetric molecule with D∞h symmetry. Surrounded by two oxygens, carbon is the central atom. MO therory predicts π bond formation resulting from the interaction of C 2Px and y atomic orbitals with O fragment LGO(Ligand Group Orbitals).
Introduction
Carbon dioxide is a well studied molecule. Carbon dioxide is a covalent compound comprised of three atoms, carbon surrounded by two oxygens. Both carbon and oxygen contain p orbitals that are able to interact based on symmetry compatability. Valence bond (VB) theory predicts four bonds for carbon and two for each oxygen. The bond order of each carbon-oxygen bond is 2. Carbon dioxide contains two double bonds. Each double bond is comprised of one sigma bond and one π bond. Carbon dioxide is an important reagent used in industry, is a cental aspect of our global carbon cycle and is the basis for climate change. Lastly, Molecular Orbital (MO) theory is a better tool to use than VB theory because it does not assume localization of electrons. MO theory is based on Linear Combinations of Atomic Orbitals (LCAO).
MO Theory
Mo theory is used to predict bonding, anti-bonding and non-bonding orbitals. Anti-bonding orbitals are always higher in energy than corresonding bonding orbitals. Anti-bonding orbitals are usually indicated with an *. For example, σ*=sigma anti-bonding and σ=sigma bonding. Bonding can be thought of as atomic orbitals being in phase (constructive) and anti-bonding as being out of phase (destructive). Mo diagrams are graphical representations of orbital interactions based on symmetry compatability. Mo diagrams are based on individual atom electron configurations. For example, B=1s22s22p1. Boron has three valence electrons (highest n=principle quantum number in nS or nP) and 2 core electrons. Diatomic Boron (B2) has an MO diagram:
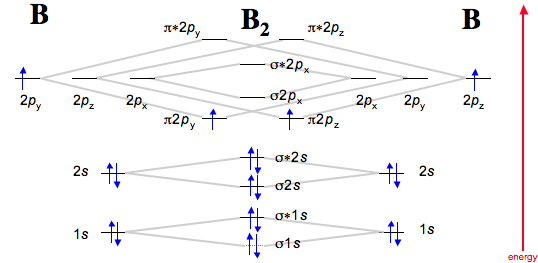
http://www.meta-synthesis.com/webbook/39_diatomics/diatomics.html
Notice that each individual B atom has 3 valence(n=2) electrons. When combined to form molecular orbitals the bond order is 1: BO=1/2(Bonding-Anti).
Carbon Dioxide MO diagram
The carbon dioxide MO diagram is based on a C atom and an O--O ligand fragment. Carbon has 2S and 2Px,y,z orbitals and the O--O fragment has 2S and 2Px,y,z orbitals that are involved in the formation of molecular orbitals. Since CO2 has D∞h symmetry the central atom's orbital symmetry lables can be obtained from the corresponding point group table: 2S=σg, 2Pz=σu and 2Px,y=πu. The LGO symmetry lables can be calculated using the point group table as well: Γσ=2σg + 2σu and Γπ=2πg + 2πu. The MO diagram for CO2 is more complicated than the diagram for B2. The follwing diagram fails to label orbital symmetries but the LGO 2Px,y particpate in the formation of π double bonds. The 2πg orbiatls are nonbonding because the C 2Px,y atomic orbitals are πu. The LGO 2Pz orbitals are involved in σ bonds.

http://cnx.org/content/m32935/latest/
Ater the formation of σ bonds resulting from C 2S and 2Pz electrons with O 2S and 2Pz orbitals the remaining C 2Px and 2Py orbitals interact with the O LGO fragment. Qualitatively, πu(2Px,y) is dipected by the MO diagram as dumbbells overlaping in phase and πg(2Px,y)* as overlapping out of phase.
References
- Housecroft, C.E., and Sharpe, A.G., Inorganic Chemistry, 3rd edition, Pearson Education Limited, Edinburgh, 2008.
- McQuarrie D.A., and Simon, J.D., Physical Chemistry A Molecular Approach, University Science Books, 1997.
Outside Links
- This is not meant for references used for constructing the module, but as secondary and unvetted information available at other site
- Link to outside sources. Wikipedia entries should probably be referenced here.
Problems
What does the g subscipt stand for in σg?
answer: The g implies symmetric with respect to inversion throught the center of the molecule.
Is carbon dioxide centrosymmetric? Does it have an inversion center?
answer: Yes carbon dioxide in centrosymmetric and includes an inversion center.
Contributors and Attributions
- Name #1 here (if anonymous, you can avoid this) with university affiliation

