10.1: Evidence for Electronic Structures
- Page ID
- 151415
This section describes the types of experimental data that give us hints about the electronic structure of coordination complexes (ie the molecular orbitals, their energy levels, and electron configurations). The types of experimental observations discussed here have been used to generate the theories of bonding that are described later in this chapter.
Introduction
The frontier (valence) electrons and orbitals define the chemical and physical properties of any compound. In the transition metals and their coordination compounds, the \(d\) orbitals and \(d\) electrons are the ones of interest. Thus, the \(d\) orbitals and electrons will be the focus of this chapter.
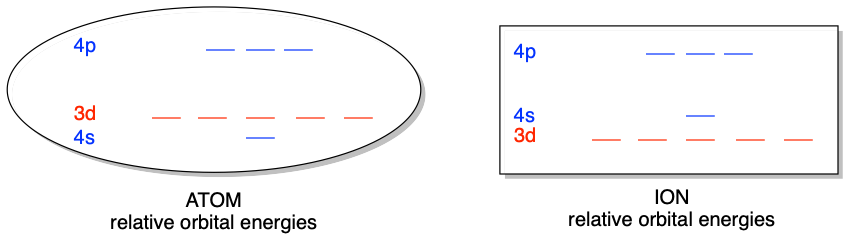
One of the first things you might notice about valence \(d\) orbitals is the order of orbital energy levels of atoms and ions in the transition metals. For example, in the first row of transition metals, the 4s orbital fills before the \(3d\) in the atoms. This indicates that \(4s\) is lower in energy than \(3d\) in these atoms. However, in the ions of the same elements, the \(3d\) orbital is occupied while the \(4s\) orbital is empty. This indicates the opposite, that the \(3d\) orbital is lower in energy than \(4s\) in these ions. The change in the relative energy levels of the \(3d\) and \(4s\) orbitals in atoms compared to ions is a result of the combined effects of shielding and penetration, as discussed in a previous chapter. The result is that the 3d and 4s orbital energy levels are close enough in energy that subtle changes in the environment can reverse the order.
Furthermore, you are going to see that once the atom is surrounded by ligands, the five \(d\) orbitals are no longer degenerate. In a coordination compound, with ligands bound in a specific geometry, the \(d\) orbitals become split into slightly different energy levels. The splitting pattern depends on where the ligands are in space; in other words it depends on the coordination geometry. The patterns of splitting for tetrahedral and octahedral geometries are shown below. Notice that the splitting is reversed between metals in a tetrahedral coordination environment compared to an octahedral environment.
When the orbitals of a coordination compound are filled with electrons, the electron configuration depends on the energy difference between the lower and higher energy levels. For example, given five \(d\) electrons in an octahedral environment, there are two possible electron configurations. All five electrons may occupy the lower level of \(d\) orbitals (Fig. \(\PageIndex{3}\), left), so that some electrons are paired. Another possibility is that all the electrons will be unpaired if they populate both levels of the d orbitals (Fig. \(\PageIndex{3}\), right).
A number of factors determine which case results, including the identity of the metal ion and the nature of the ligands involved. These different filling orders have consequences, too. The magnetic properties of the complex, its propensity to undergo reactions, and its optical properties all depend on the configuration of these frontier electrons.
This chapter is an exploration of the nature of the metal-ligand bond and how both geometry and the mode of bonding influence the properties of coordination complexes.
- 10.1.2: Magnetic Susceptibility
- The electronic structure of coordination complexes can lead to several different properties that involve different responses to magnetic fields. These properties can vary between related compounds because of differences in electron counts, geometry, or donor strength. As a result, magnetic measurement of these materials can be used as a tool to provide insight into the structure of a coordination complex.


