Skip to main content
Chemistry LibreTexts

2.2: Problem Set 2

  1. Last updated
  2. Save as PDF
  • Page ID
    221685

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Do Problem 7.1, p. 201 in Cotton (3rd ed).

    2. Do Problem 6.1, p. 129 in Cotton (3rd ed), and then solve the appropriate secular determinant to find the energies of the 10 MOs spanned by the SALCs you have derived.

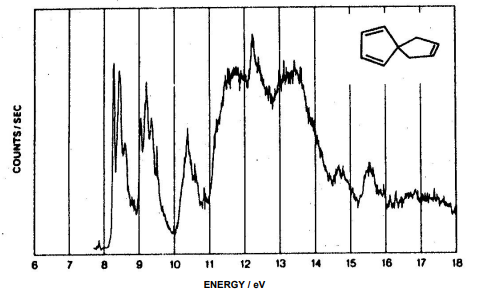
    3. Construct the MO diagram for the molecule shown below and assign the photoelectron spectrum.

    clipboard_e2b1aef2636386e98e77d3e5fc23616ef.png

    4. A Hückel analysis may also be used to describe σ-bonding. Consider the three center bond of the Al2(µ-CH3)2 unit in “trimethyl aluminum” which exists as the dimer [Al(CH3)3]2 in the gas phase and nonpolar solvents.

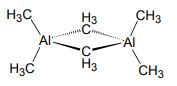
    clipboard_e3eab1643997d3ac452be6e6481f5a56a.png

    a. Using the 6 σ orbitals shown below, determine the basis for the four Al σ-bonds.

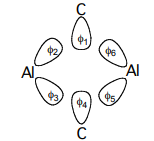
    clipboard_e95940d10a2aa65e6dc6099340914ffd1.png

    b. Construct the SALC’s using the projection operator method.

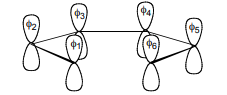
    c. Follow the same procedure for the carbon σ-bonds.

    d. Determine the energy levels of the molecular orbital diagram.

    e. Give the explicit expressions for the six molecular orbitals of the Al2(µ-CH3)2 unit.

    5. Consider 1,3,5-hexatriene and benzene.

    a. For the former construct the MO diagram; calculate the delocalization energy; and construct the molecular orbital eigenfunctions.

    b. 1,3,5-hexatriene and benzene are limiting cases for a more general molecular orbital system in which the interaction energy for the terminal orbitals, β1,6, is finite and not equal to the interaction energy between adjacent orbitals.

    clipboard_e55f1627df10d19c75781a0730caafd1b.png

    c. Determine the molecular orbital energies of the general C6 system (i.e. β1,6 ≠ βi,j (i,j ≠ 1,6) and show that in the limiting regimes of this general case, the MO diagrams. For 1,3,5- hexatriene and benzene are obtained.

    d. Draw a correlation diagram.

    This page titled 2.2: Problem Set 2 is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Daniel Nocera via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.