Skip to main content
Chemistry LibreTexts

2.1: Problem set 1

  1. Last updated
  2. Save as PDF
  • Page ID
    221684

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Determine the general matrix rep for a σv at angle from the xz plane on a point (x1,y1,z1) at angle from the xz plane. Provide matrix reps for the 3σv in C3v.

    2. Consider the generators C5 and h.

    1. What group is generated from these two operations?
    2. Construct a multiplication table.
    3. Determine the classes in the group.
    4. Do C5 and σh commute? Show both by matrix algebra and by operating on a vector (x1,y1,z1).

    3. Do the following problems in Cotton (3rd edition): A3.2, A3.4, 4.4 and 4.7.

    4. Consider the trigonal planar molecule, BF3. Use the three fluorine atoms as an arbitrary basis set to describe the matrix representation for each of the operations in the point group (relying on the methods employed above, solve the appropriate eigenvalue problem).

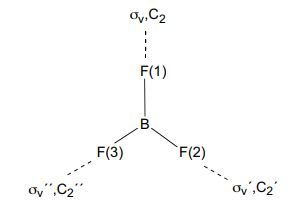
    clipboard_e1723cd915bc8cb4863735fadde3f9e10.png

    1. Construct the matrix representations for the operations in the D3h point group.
    2. Find the three eigenvalues λi and normalize the eigenvectors for the C3 matrix representation (Hint: The eigenvectors are orthogonal to each other. For complex eigenvectors, remember that the normalization is defined as A*A where A* is the complex conjugate).
    3. Construct the similarity transformation matrix θ from the eigenvectors and determine θ-1 . For the case where the eigenvectors are complex, take linear combinations to yield eigenvectors in real space. θ-1 is the adjoint of θ divided by the determinant. See pg 424 in Cotton for the definition of an adjoint.
    4. Using θ and θ–1 block-diagonalize the matrices in Part (a) and calculate the characters of the irreducible representations for the given basis.
    5. To what irreducible representations do the F atom basis functions belong?
    6. Complete the D3h character table using the algebraic rules governing irreducible representations. Show work.

    5. Assign point groups to the following molecules. Sketch the molecule and the symmetry elements present in each.

    1. ethane (staggered)
    2. ethane (eclipsed)
    3. cyclohexane (chair)
    4. cyclohexane (boat)
    5. adamantane
    6. ferrocene (staggered)
    7. ferrocene (eclipsed)
    8. P4
    9. S8

    6. Draw a molecule (not found in the texts or lecture notes) that exemplifies each of the following point groups. Please use molecules that actually exist.

    1. C2h
    2. D8h
    3. D2d
    4. CS
    5. C6v

    This page titled 2.1: Problem set 1 is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Daniel Nocera via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.