1.13: Octahedral ML₆ π complexes
- Page ID
- 221681
The basis set needs to be expanded for metal complexes with ligands containing π orbitals. An appropriate basis for ligands with two orthogonal π orbitals, e.g. CO, CN– , O2–, X– , to the σ bond is shown below,
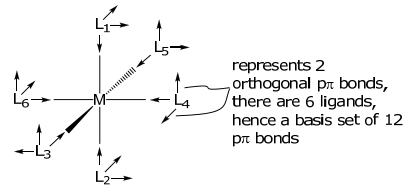
The arrow is indicative of the directional phase of the pπ orbitals. Owing to their ungerade symmetry, in constructing the pπ representation
- a p orbital, i.e. arrow, that transforms into itself contributes +1
- a p orbital that transforms into minus itself contributes –1
- a p orbital that moves, contributes 0
$$
\begin{array}{c|cccccccccc}
\mathrm{O}_{\mathrm{h}} & \mathrm{E} & 8 \mathrm{C}_{3} & 6 \mathrm{C}_{2} & 6 \mathrm{C}_{4} & 3 \mathrm{C}_{2} & \mathrm{i} & 6 \mathrm{~S}_{4} & 8 \mathrm{~S}_{6} & 3 \sigma_{\mathrm{h}} & 6 \sigma_{\mathrm{d}} \\
\hline \Gamma_{\sigma} & 6 & 0 & 0 & 2 & 2 & 0 & 0 & 0 & 4 & 2 & \rightarrow \mathrm{a}_{19}+\mathrm{t}_{1 \mathrm{u}}+\mathrm{e}_{\mathrm{g}} \\
\Gamma_{\pi} & 12 & 0 & 0 & 0 & -4 & 0 & 0 & 0 & 0 & 0 & \rightarrow \mathrm{t}_{1 \mathrm{~g}}+\mathrm{t}_{1 \mathrm{u}}+\mathrm{t}_{2 \mathrm{~g}}+\mathrm{t}_{2 \mathrm{u}}
\end{array}
\]
There is a second method to derive the pπ basis. The Cartesian coordinate systems on each ligand contains the σ and π basis sets. Thus the Γx,y,z irreducible representation (which is the sum of Γx + Γy + Γz or Γz + Γx,y for irreducible representations for which x,y,z are not triply degenerate) defines the 1σ and 2pπ bonds of each ligand. Since the bond is coincident with the ligand, an unmoved atom is approximated by Γσ. On the basis of geometrical considerations, the following is true,
$$
\begin{aligned}
&\underset{\text { atomoved }}{\Gamma_{\text {atoms }}}=\Gamma_{\sigma} \\
&\Gamma_{\sigma+\pi}=\Gamma_{\mathrm{x}, y, z} \cdot \Gamma_{\sigma} \\
&\Gamma_{\pi}=\Gamma_{\sigma+\pi}-\Gamma_{\sigma}
\end{aligned}
\]

The σ SALCs have already been derived in Lecture 12. Methods 1-3 of Lecture 12 can be employed to determine the pπ SALCs. For the orbitals that transform as t1u and t2g, Method 3 (mirror the metal atomic orbital symmetry) is convenient. For the t1u SALC,
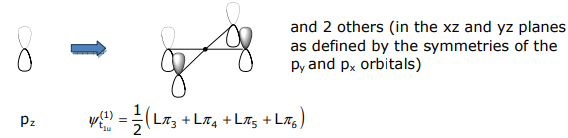
The t2g SALCs have the mirrored symmetry of the (dxy,dxz,dyz) orbital set,
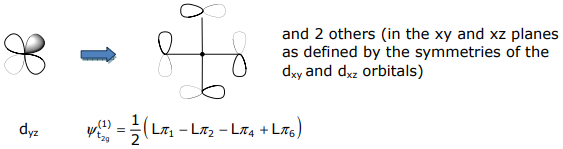
Non-bonding SALCs must be ascertained from projection operators and Schmidt orthogonalization methods.
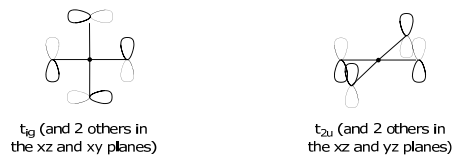
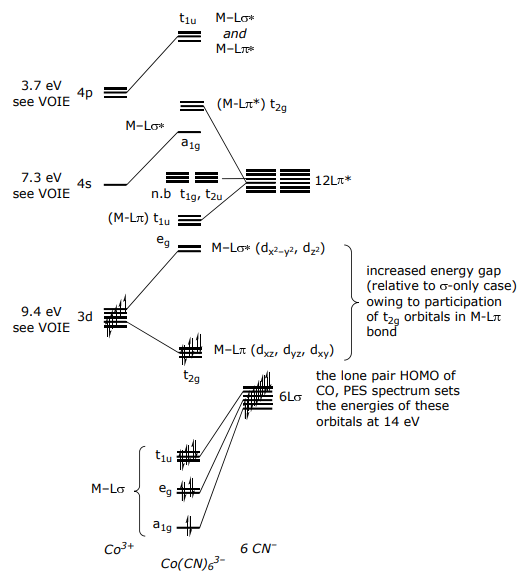
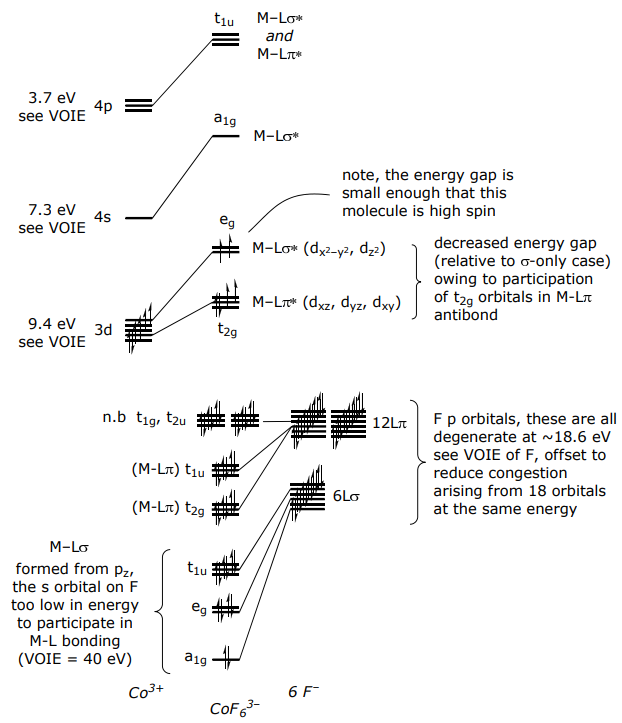
For a π donor complex such as CoF6 3–,
For a π-accepting ligand set, orbitals have the same form (or symmetry) as π donors,
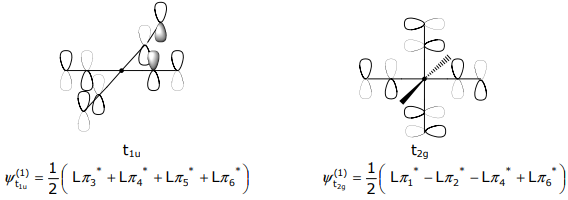
The only difference between the π-donor and π-acceptor MO diagrams is the relative placement of the π* orbitals relative to the metal atomic orbitals; for Co(CN)6 3–,