5.3: Crystal Field Theory
- Page ID
- 183319
Crystal field theory is one of the simplest models for explaining the structures and properties of transition metal complexes. The theory is based on the electrostatics of the metal-ligand interaction, and so its results are only approximate in cases where the metal-ligand bond is substantially covalent. But because the model makes effective use of molecular symmetry, it can be surprisingly accurate in describing the magnetism, colors, structure, and relative stability of metal complexes.
Consider a positively charged metal ion such as Fe3+ in the "field" of six negatively charged ligands, such as CN-. There are two energetic terms we need to consider. The first is the electrostatic attraction between the metal and ligands, which is inversely proportional to the distance between them:
\[E_{elec} = \frac{1}{4\pi\varepsilon_{0}} \sum_{ligands} \frac{q_{M}q_{L}}{r_{ML}}\]
The second term is the repulsion that arises from the Pauli exclusion principle when a third electron is added to a filled orbital. There is no place for this third electron to go except to a higher energy antibonding orbital. This is the situation when a ligand lone pair approaches an occupied metal d-orbital:
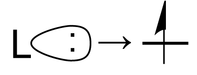
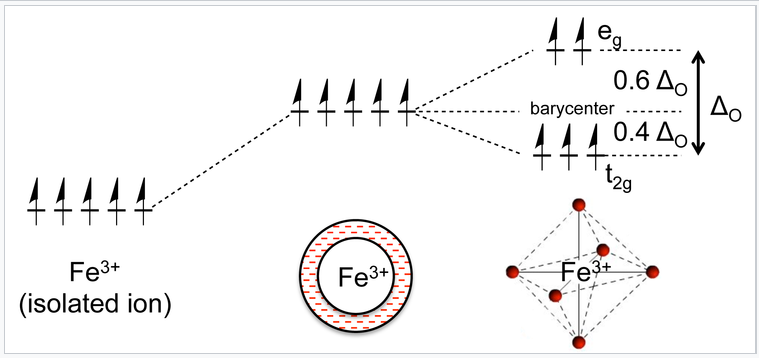
Now let us consider the effect of these attractive and repulsive terms as the metal ion and ligands are brought together. We do this in two steps, first forming a ligand "sphere" around the metal and then moving the six ligands to the vertices of an octahedron. Initially all five d-orbitals are degenerate, i.e., they have the same energy by symmetry. In the first step, the antibonding interaction drives up the energy of the orbitals, but they remain degenerate. In the second step, the d-orbitals split into two symmetry classes, a lower energy, triply-degenerate set (the t2g orbitals) and a higher energy, doubly degenerate set (the eg orbitals).
|
A Fe3+ ion has five d-electrons, one in each of the five d-orbitals. In a spherical ligand field, the energy of electrons in these orbitals rises because of the repulsive interaction with the ligand lone pairs. The orbitals split into two energy levels when the ligands occupy the vertices of an octahedron, but the average energy remains the same. |
The energy difference between the eg and t2g orbitals is given the symbol ΔO, where the "O" stands for "octahedral." We will see that this splitting energy is sensitive to the degree of orbital overlap and thus depends on both the metal and the ligand. Relative to the midpoint energy (the barycenter), the t2g orbitals are stabilized by 2/5 ΔO and the eg orbitals are destabilized by 3/5 ΔO in an octahedral complex.
|
d-orbitals and their orientation with relation to ligands in an octahedral complex. |
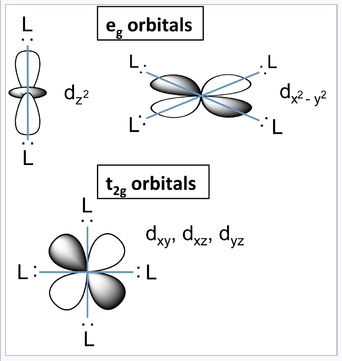
What causes the d-orbitals to split into two sets? Recall that the d-orbitals have a specific orientation with respect to the Cartesian axes. The lobes of the dxy, dxz, and dyz orbitals (the t2g orbitals) lie in the xy-, xz-, and yz-planes, respectively. These three d-orbitals have nodes along the x-, y-, and z-directions. The orbitals that contain the ligand lone pairs are oriented along these axes and therefore have zero overlap with the metal t2g orbitals. It is easy to see that these three d-orbitals must be degenerate by symmetry. On the other hand, the lobes of the dz2 and dx2-y2 orbitals (the eg orbitals) point directly along the bonding axes and have strong overlap with the ligand orbitals. While it is less intuitively obvious, these orbitals are also degenerate by symmetry and have antibonding character.
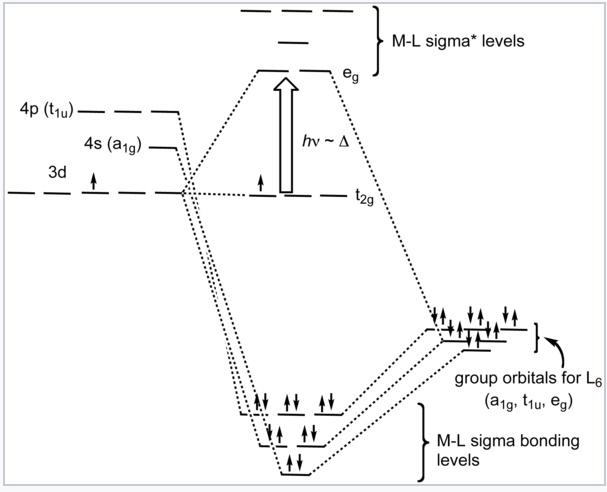
It is informative to compare the results of crystal field theory and molecular orbital theory (also called ligand field theory in this context) for an octahedral transition metal complex. The energy level diagrams below make this comparison for the d1 octahedral ion [Ti(H2O)6]3+. In the MO picture below, the frontier orbitals are derived from the metal d-orbitals. The lower t2g set, which contains one electron, is non-bonding by symmetry, and the eg orbitals are antibonding. The metal 4s orbital, which has a1g symmetry, makes a low energy bonding combination that is ligand-centered, and an antibonding combination that is metal-centered and above the eg levels. This is the reason that our d-electron counting rules do not need to consider the metal 4s orbital. The important take-home message is that crystal field theory and MO theory give very similar results for the frontier orbitals of transition metal complexes.
|
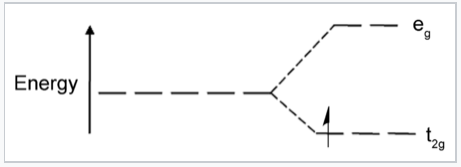
Crystal field energy diagram for the d1 octahedral complex [Ti(H2O)6]3+. |
|
Ligand-field diagram for the octahedral complex [Ti(H2O)6]3+. |