2.6: Orbital Filling
- Page ID
- 183301
MO’s are filled from the bottom according to the Aufbau principle and Hund’s rule, as we learned for atomic orbitals.
Question: what is the quantum mechanical basis of Hund’s rule?
- Consider the case of two degenerate orbitals, such as the π or π* orbitals in a second-row diatomic molecule. If these orbitals each contain one electron, their spins can be parallel (as preferred by Hund's rule) or antiparallel. The Pauli exclusion principle says that no two electrons in an orbital can have the same set of quantum numbers (n, l, ml, ms). That means that, in the parallel case, the Pauli principle prevents the electrons from ever visiting each other's orbitals. In the antiparallel case, they are free to come and go because they have different ms quantum numbers. However, having two electrons in the same orbital is energetically unfavorable because like charges repel. Thus, the parallel arrangement, thanks to the Pauli principle, has lower energy.
For O2 (12 valence electrons), we get the MO energy diagram below. The shapes of the molecular orbitals are shown at the right.
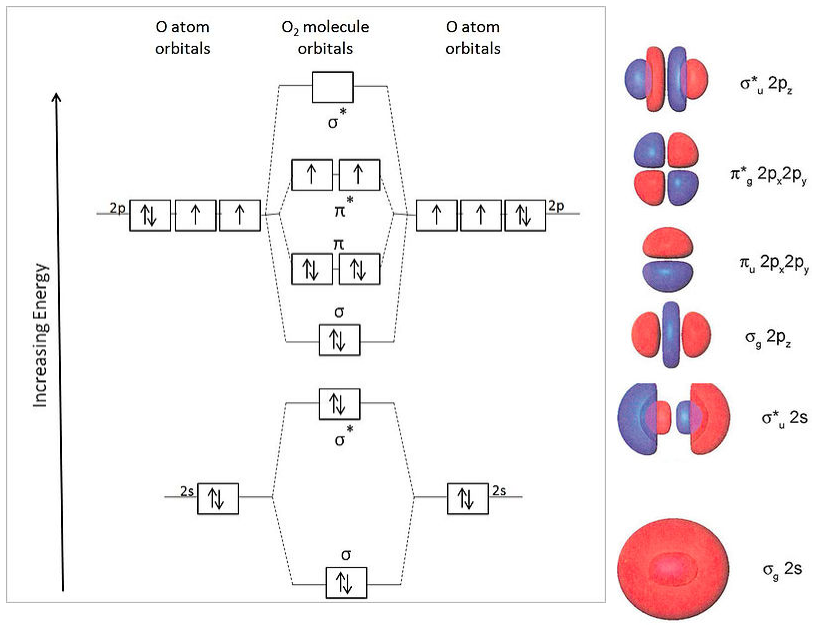
This energy ordering of MOs correctly predicts two unpaired electrons in the π* orbital and a net bond order of two (8 bonding electrons and 4 antibonding electrons). This is consistent with the experimentally observed paramagnetism of the oxygen molecule.
Other interesting predictions of the MO theory for second-row diatomics are that the C2 molecule has a bond order of 2 and that the B2 molecule has two unpaired electrons (both verified experimentally).
We can also predict (using the O2, F2, Ne2 diagram above) that NO has a bond order of 2.5, and CO has a bond order of 3.
The symbols "g" and "u" in the orbital labels, which we only include in the case of centrosymmetric molecules, refer to their symmetry with respect to inversion. Gerade (g) orbitals are symmetric, meaning that inversion through the center leaves the orbital unchanged. Ungerade (u) means that the sign of the orbital is reversed by the inversion operation. Because g and u orbitals have different symmetries, they have zero overlap with each other. As we will see below, factoring orbitals according to g and u symmetry simplifies the task of constructing molecular orbitals in more complicated molecules, such as butadiene and benzene.
The orbital shapes shown above were computed using a one-electron model of the molecule, as we did for hydrogen-like AOs to get the shapes of s, p, and d-orbitals. To get accurate MO energies and diagrams for multi-electron molecules (i.e. all real molecules), we must include the fact that electrons are “correlated,” i.e. that they avoid each other in molecules because of their negative charge. This problem cannot be solved analytically, and is solved approximately in numerical calculations by using density functional theory (DFT). We will learn about the consequences of electron correlation in solids (such as superconductors) in Chapter 10.
|
Red giant stars are characterized by the presence of C2 molecules in their atmospheres. Since C2 has a net bond order of two, it reacts rapidly as it cools from the gas phase to make other forms of carbon such as fullerenes, graphite, and diamond, all of which have four bonds for every two carbon atoms. |



