9.1: Ionic Radii and Radius Ratios
- Page ID
- 183346
Atoms in crystals are held together by electrostatic forces, van der Waals interactions, and covalent bonding. It follows that arrangements of atoms that can maximize the strength of these attractive interactions should be most favorable and lead to the most commonly observed crystal structures.
Radius ratio rules
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was (and still is!) important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
|
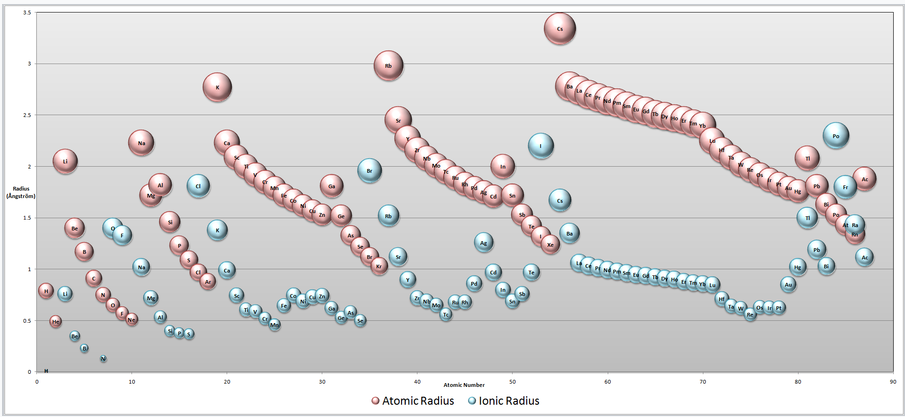
Atomic and Ionic Radii. Note that cations are always smaller than the neutral atom (pink) of the same element, whereas anions are larger. Going from left to right across any row of the periodic table, neutral atoms and cations contract in size because of increasing nuclear charge. (click for larger image) |
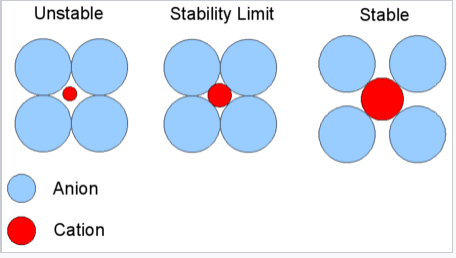
The basic idea of radius ratio rules is illustrated at the right. We consider that the anion is the packing atom in the crystal and the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbor anions, as shown at the right for a small cation in contact with larger anions, then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
|
Critical Radius Ratio. This diagram is for coordination number six: 4 anions in the plane are shown, 1 is above the plane and 1 is below. The stability limit is at rC/rA = 0.414 |
| Coordination number | Geometry | ρ = rcation/ranion |
|---|---|---|
| 2 | linear | 0 - 0.155 |
| 3 | triangular | 0.155 - 0.225 |
| 4 | tetrahedral | 0.225 - 0.414 |
| 4 | square planar | 0.414 - 0.732 |
| 6 | octahedral | 0.414 - 0.732 |
| 8 | cubic | 0.732 - 1.0 |
| 12 | cuboctahedral | 1.0 |
There are unfortunately several challenges with using this idea to predict crystal structures:
- We don't know the radii of individual ions
- Atoms in crystals are not really ions - there is a varying degree of covalency depending electronegativity differences
- Bond distances (and therefore ionic radii) depend on bond strength and coordination number (remember Pauling's rule D(n) = D(1) - 0.6 log n)
- Ionic radii depend on oxidation state (higher charge => smaller cation size, larger anion size)
We can build up a table of ionic radii by assuming that the bond length is the sum of the radii (r+ + r-) if the ions are in contact in the crystal. Consider for example the compounds MgX and MnX, where X = O, S, Se. All of these compounds crystallize in the NaCl structure:
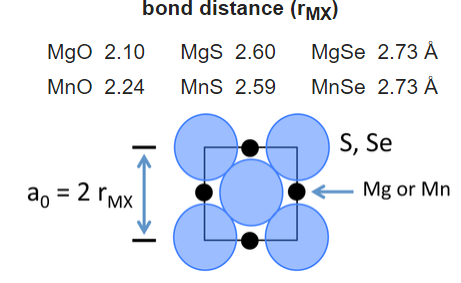
For the two larger anions (S2- and Se2-), the unit cell dimensions are the same for both cations. This suggests that the anions are in contact in these structures. From geometric considerations, the anion radius in this case is given by:
\[r_{_}= \frac{r_{MX}}{\sqrt{2}}\]
and thus the radii of the S2- and Se2- ions are 1.84 and 1.93 Å, respectively. Once the sizes of these anions are fixed, we can obtain a self-consistent set of cation and anion radii from the lattice constants of many MX compounds.
How well does this model work? Let's consider the structures of tetravalent metal oxides (MO2), using Pauling radii and the predictions of the radius ratio model:
| Oxide MO2 | Radius ratio | Predicted coord. no. | Observed coord no. (structure) |
|---|---|---|---|
| CO2 | ~0.1 | 2 | 2 (linear molecule) |
| SiO2 | 0.32 | 4 | 4 (various tetrahedral structures) |
| GeO2 | 0.43 | 4 | 4 (silica-like structures) |
| " | 0.54 | 6 | 6 (rutile) |
| TiO2 | 0.59 | 6 | 6 (rutile) |
| ZrO2 | 0.68 | 6 | 7 (baddleyite) |
| " | 0.77 | 8 | 8 (fluorite) |
| ThO2 | 0.95 | 8 | 8 (fluorite) |
Note that cations have different radii depending on their coordination numbers, and thus different radius ratios are calculated for Ge4+ with coordination numbers 4 and 6, and for Zr4+ with coordination numbers 6 and 8.
For this series of oxides, the model appears to work quite well. The correct coordination number is predicted in all cases, and borderline cases such as GeO2 and ZrO2 are found in structures with different coordination numbers. The model also correctly predicts the structures of BeF2 (SiO2 type), MgF2 (rutile), and CaF2 (fluorite).
What about the alkali halides NaCl, KBr, LiI, CsF, etc.? All of them have the NaCl structure except for CsCl, CsBr, and CsI, which have the CsCl (8-8) structure. In this case the radius ratio model fails rather badly. The Li+ salts LiBr and LiI are predicted to have tetrahedral structures, and KF is predicted to have an 8-8 structure like CsCl. We can try adjusting the radii (e.g., making the cations larger and anions smaller), but the best we can do with the alkali halides is predict about half of their structures correctly. Since the alkali halides are clearly ionic compounds, this failure suggests that there is something very wrong with the radius ratio model, and its success with MO2 compounds was coincidental.
In addition to the radius ratio rule, Linus Pauling developed other useful rules that are helpful in rationalizing and also predicting the structures of inorganic compounds. Pauling's rules[1] state that:
- Stable structures are locally electroneutral. For example, in the structure of the double perovskite Sr2FeMoO6, MO6 (M = Fe2+, Mo6+) octahedra share all their vertices, and Sr2+ ions fill the cubooctahedral cavities that are flanked by eight MO6 octahedra.[2] Each O2- ion is coordinated to one Fe2+ and one Mo6+ ion in order to achieve local electroneutrality, and thus the FeO6 and MoO6 octahedra alternate in the structure.
- Cation-cation repulsion should be minimized. Anion polyhedra can share vertices (as in the perovskite structure) without any energetic penalty. Shared polyhedral edges, and especially shared faces, cause cation-cation repulsion and should be avoided. For example, in rutile, the most stable polymorph of TiO2, the TiO6 octahedra share vertices and two opposite edges, forming ribbons in the structure. In anatase TiO2, each octahedron shares four edges so the anatase polymorph is less thermodynamically stable.
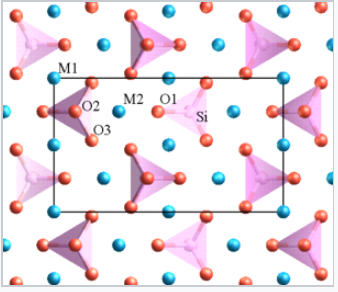
- Highly charged cations in anion polyhedra tend not to share edges or even vertices, especially when the coordination number is low. For example, in orthosilicates such as olivine (M2SiO4), there are isolated SiO44- tetrahedra.
|
Structure of olivine. M (Mg or Fe) = blue spheres, Si = pink tetrahedra, O = red spheres. |
As we will soon see, all of Pauling's rules are justified on the basis of lattice energy considerations. In ionic compounds, the arrangement of atoms that maximizes anion-cation interactions while minimizing cation-cation and anion-anion contacts is energetically the best.