2.8: Isotopes of Hydrogen
- Page ID
- 212850
Physical effects
The presence of intermolecular hydrogen bonding provides additional attractive forces between molecules. Thus, properties that depend on intramolecular forces are affected.
| Isotope | Hydrogen-1 | Hydrogen-2 | Hydrogen-3 |
|---|---|---|---|
| Special name | Hydrogen | Deuterium | Tritium |
| Symbol | H | D | T |
| Atomic number |
1 |
1 | 1 |
| Number of neutrons | 0 | 1 | 2 |
| Mass number | 1 | 2 | 3 |
| Natural abundance | 99.9844% | 0.0156% | very small |
Synthesis of deuterium compounds
Electrolysis of water
The electrolysis of hydrogen-1 water (H2O) in the presence of an alkali results in the formation of hydrogen and oxygen.
\[ 2 H_2O_{(l)} \rightarrow 2H_{2(g)} + O_{2(g)} \]
In a similar manner the hydrolysis of deuterated water (D2O) yields deuterium and oxygen.
\[ 2D_2O_{(l)} \rightarrow 2 D_{2(g)} + O_{2(g)} \]
However, the rate of electrolysis of D2O is slightly slower than that of H2O. Thus, the partial hydrolysis of water with a mixture of natural isotopes results in the slight enrichment of the water with D2O. The level of enrichment in one step is less than 1%. In order to obtain high levels of D2O (e.g., ca. 30%) it is necessary to reduce the original volume of water by 1/100,000th.
Chemical equilibrium
Proton exchange reactions can be used to enrich compounds in deuterium. For example, the reaction of HSD with water shown in (2.8.3) has a slight preference for the formation of H2S, i.e., Keq = 1.012. Thus, bubbling HSD through water results in the enrichment of the water in HOD. However, about 30% enrichment is about the best that can be achieved by this method.
\[ H_2O_{(l)} + HSD_{(g)} \leftrightharpoons HOD_{(l)} + H_2S_{(g)} \]
Fractional distillation
The boiling point of H2O is (by definition) 100 ◦C, in contrast the boiling point of D2O is 101.4 ◦C. Thus, it is possible to separate H2O from D2O by fractional distillation. This method provides the most suitable route to high isotopic enrichment and D2O of 99.8% can be produced this way.
Note
The term heavy water is used for D2O of greater than 99.8% enrichment.
Uses of deuterium compounds
Possible nuclear fusion
The largest use of D2O is as a moderator and heat exchanger for fission nuclear reactors, however, the biggest potential application will be if nuclear fusion is realized as a commercial process.
The fusion of two deuterium atoms to form a helium atom and energy would be one source of energy, (2.8.4), however, deuterium-tritium fusion is the most promising, (2.8.5).
\[ ^2_1H + ^2_1H \rightarrow ^3_2He + ^1_0n +energy \]
\[ ^2_1H + ^3_1H \rightarrow ^4_2He + ^1_0n +energy \]
The deuterium part of the fuel does not pose a great problem because about 1 part in 5000 of the hydrogen in seawater is deuterium. This amounts to an estimate that there is over 1015 tons of deuterium in the oceans. The tritium part of the fuel is more problematic since there is no significant natural source (Table \(\PageIndex{2}\).9), and the tritium would have to be obtained by breeding the tritium from lithium.
\[ ^6_3Li + ^1_0n \rightarrow ^4_2He + ^3_1H\]
Since a gallon of seawater could produce as much energy as 300 gallons of gasoline, there is clearly a large amount of energy that can potentially be realized through nuclear fusion. Unfortunately, this advantage is also a disadvantage since the temperatures attained are similar to the surface of the sun, which would vaporize any conventional container. Fusion experiments therefore use a magnetic field to contain the reaction. The shape of the eld is like a bottle, hence the term "magnetic bottle".
One demonstrated fusion process is the so-called hydrogen bomb or thermonuclear bomb in which a fission atom bomb is used to initiate a fusion reaction. The atomic bomb is surrounded by a layer of lithium deuteride. Neutrons from the atomic explosion (fission) cause the lithium to be converted into helium, tritium, and energy, (2.8.6). The atomic explosion also supplies the 50,000,000 ◦C temperature needed for the subsequent fusion of deuterium with tritium, (2.8.5). So in-fact the hydrogen bomb is misnamed and it should be called a deuterium bomb.
Note
The original calculations to model the hydrogen bomb were performed using ENIAC (short for Electronic Numerical Integrator And Computer) that was originally designed to generate tables of trajectories of shells red from large artillery. The artillery ring tables were made by women mathematicians who were called calculators hence the name used today. Built in 1946 ENIAC is often assumed to be the first programmable electronic computer, however, it was predated by the six Colossus machines that were used to successfully crack the German Enigma code as early as 1944. However, the existence of the Colossus machines was kept secret until 1975.
Spectroscopy
In the chemical laboratory deuterium compounds are commonly used in spectroscopy for:
a) The assignment of resonances in IR, Raman, and NMR spectroscopy.
b) As a non-proton containing solvent in 1H NMR spectroscopy.
A description of these applications is given below.
Reaction mechanism and rate determination
Given the larger mass of deuterium over hydrogen there is an associated dierence in the rate of reactions (see below) and therefore investigations using hydrogen and deuterium analogs can provide information as to reaction mechanisms.
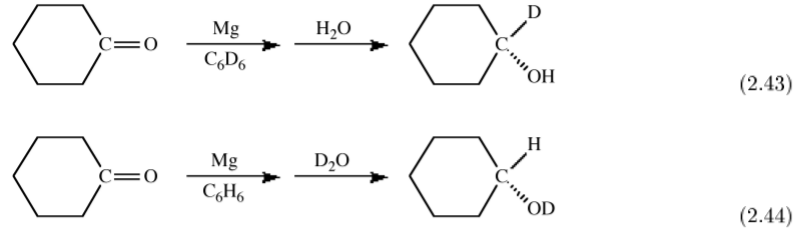
The spectroscopic dierences between hydrogen and deuterium can also be used as a tracer to uniquely determine the source of particular substituents. For example, the magnesium (or Grignard) reduction of a ketone yields upon hydrolysis the secondary alcohol. If the reaction is carried out in a deuterated solvent and H2O used for hydrolysis then the secondary carbon is deuterated, (2.43). In contrast, if the reaction is carried out in a non-deuterated solvent and hydrolysis is accomplished with D2O then the deuterated alcohol is formed, (2.44). These experiments define that the initial reduction occurs at the ketone's α-carbon.
Exercise \(\PageIndex{1}\)
Given the following reactions and the isotope distribution of the products suggest the reaction mechanism.
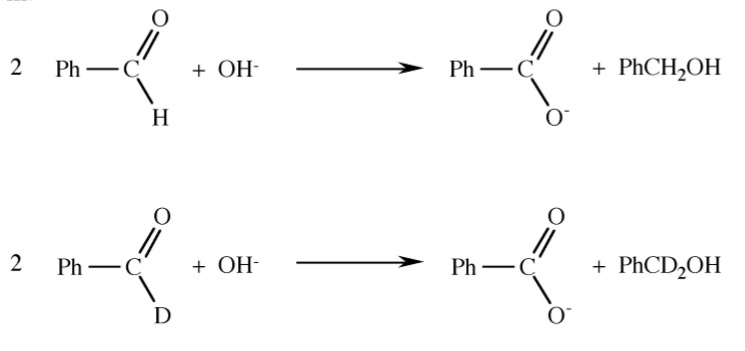
- Answer
-

Differences between hydrogen and deuterium
Properties that depend on nuclei properties
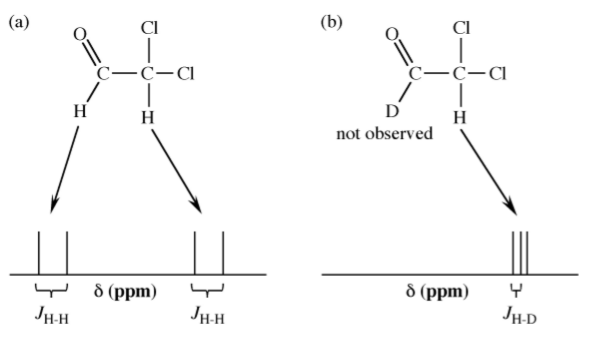
The nuclear magnetic moment of an atomic nucleus arises from the spins of the protons and neutrons within the nucleus. As a consequence the magnetic moment for hydrogen and deuterium are very different and hence the conditions for detection by NMR are very different. Thus, in observing the 1H NMR spectrum of a compound not only are the deuterium atoms not observed, but the coupling is now H-D rather than H-H (Figure \(\PageIndex{2}\).31).
Deuterium is better at scattering neutrons than hydrogen. The H and D cross sections are very distinct and different in sign, which allows contrast variation in such experiments. Hydrogen's low electron density makes it difficult to determine its position by X-ray diffraction methods, neutron diffraction methods allow for highly accurate structure determination. Hydrogen can be seen by neutron diffraction and scattering, however, it has a large incoherent neutron cross-section. This is nil for deuterium and thus delivers much clearer signals may be obtained for deuterated samples. Neutron scattering of deuterated samples is indispensable for many studies of macromolecules in biology.
Properties that depend on mass
The difference in mass between hydrogen and deuterium obviously results in a difference in molecular mass of their analogous compounds. This difference can be used for analysis by mass spectrometry, but it also results in different densities of compounds. For example, the density of H2O at 25 ◦C is 0.997 g/cm3, while the density of D2O at 25 ◦C is 1.104 g/cm3.
The vibrational frequency for a diatomic molecule, H-X, can be defined by the equation:
\[ v_{H-X} = \dfrac{1}{2\pi} \sqrt{\dfrac{f_{H-X}}{\mu_{H-X}}}\]
where fH-X is the H-X bond force constant, and µH-X is the reduced mass.
\[ \mu_{H-X} = \dfrac{m_h \cdot m_X}{m_H + m_X} \]
If substitute H for D the D-X force constant is the same as the H-X force constant, but the reduced mass is twice the value for the H-X bond. As a result the ratio of the vibrational frequency of an H-X bond to that of the analogous D-X bond is given by the following equation.
\[\dfrac{\mu_{D-X}}{\mu_{H-X}} = (\dfrac{\mu_{H-X}}{\mu_{D-X}})^{\dfrac{1}{2}} = \dfrac{1}{\sqrt{2}} \]
With the change in vibrational energy there is concomitant change in the bond strength.
\[ E_{D-X} > E_{H-X} \]
Thus, the rate of reactions will be faster for hydrogen derivative than the deuterium analog. The ratio of the rate constants will be dependant on the involvement of H-X bond breaking or forming in the rate limiting step (the slowest reaction step within the overall reaction mechanism). When an H-X bond is made or broken in the rate limiting step, then the ratio of the rate constants upon deuterium substitution will be:
\[ \dfrac{k_{H-X}}{k_{D-X}} \approx 7 \]
This is known as the primary isotope effect. In this case where H-X bond breaking or forming is not part of the rate limiting step, then the isotope effect will be much smaller and is known as a secondary isotope effect.
The position of equilibrium reactions that involve hydrogen exchange, (2.8.12), will be effected by the presence of deuterium to favor the deuterium being concentrated in the more stable bond. This is the basis of the concentration of HOD from HSD and water, (2.8.3).
\[ \text{X-H} + \text{Y-D} \leftrightharpoons \text{X-D} + \text{Y-H} \]
Bibliography
- M. B. Power, S. G. Bott, J. L. Atwood, and A. R. Barron. J. Am. Chem. Soc., 1990, 112, 3446.
- A. S. Borovik and A. R. Barron, Main Group Chem. 2005, 4, 135.


