11.6: Phase Equilibrium in Solutions - Volatile Solutes

Last updated
Save as PDF

Page ID: 41597

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

To understand the relationship among temperature, pressure, and solubility.
The understand that the solubility of a solid may increase or decrease with increasing temperature,
To understand that the solubility of a gas decreases with an increase in temperature and a decrease in pressure.

Effect of Pressure on the Solubility of Gases: Henry’s Law

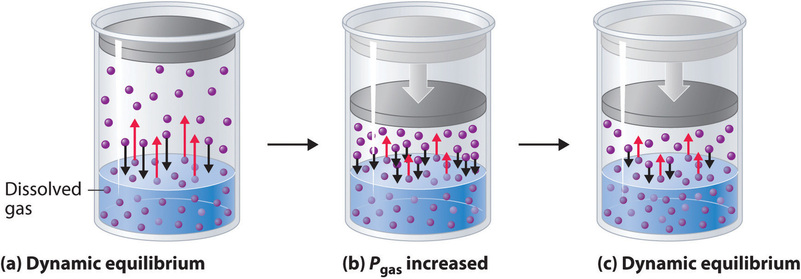
External pressure has very little effect on the solubility of liquids and solids. In contrast, the solubility of gases increases as the partial pressure of the gas above a solution increases. This point is illustrated in Figure \(\PageIndex{1}\), which shows the effect of increased pressure on the dynamic equilibrium that is established between the dissolved gas molecules in solution and the molecules in the gas phase above the solution. Because the concentration of molecules in the gas phase increases with increasing pressure, the concentration of dissolved gas molecules in the solution at equilibrium is also higher at higher pressures.

Figure \(\PageIndex{1}\): A Model Depicting Why the Solubility of a Gas Increases as the Partial Pressure Increases at Constant Temperature. (a) When a gas comes in contact with a pure liquid, some of the gas molecules (purple spheres) collide with the surface of the liquid and dissolve. When the concentration of dissolved gas molecules has increased so that the rate at which gas molecules escape into the gas phase is the same as the rate at which they dissolve, a dynamic equilibrium has been established, as depicted here. This equilibrium is entirely analogous to the one that maintains the vapor pressure of a liquid. (b) Increasing the pressure of the gas increases the number of molecules of gas per unit volume, which increases the rate at which gas molecules collide with the surface of the liquid and dissolve. (c) As additional gas molecules dissolve at the higher pressure, the concentration of dissolved gas increases until a new dynamic equilibrium is established.

The relationship between pressure and the solubility of a gas is described quantitatively by Henry’s law, which is named for its discoverer, the English physician and chemist, William Henry (1775–1836):

\[C = k_HP \label{11.61}\]

where \(C\) is the concentration of dissolved gas at equilibrium, \(P\) is the partial pressure of the gas, and \(k_H\) is the Henry’s law constant, which must be determined experimentally for each combination of gas, solvent, and temperature.

Although the gas concentration may be expressed in any convenient units, we will use molarity exclusively. The units of the Henry’s law constant are therefore mol/(L·atm) = M/atm. Values of the Henry’s law constants for solutions of several gases in water at 20°C are listed in Table \(\PageIndex{1}\).

As the data in Table \(\PageIndex{1}\) demonstrate, the concentration of a dissolved gas in water at a given pressure depends strongly on its physical properties. For a series of related substances, London dispersion forces increase as molecular mass increases. Thus among the elements of Group 18, the Henry’s law constants increase smoothly from \(\ce{He}\) to \(\ce{Ne}\) to \(\ce{Ar}\). The table also shows that \(\ce{O_2}\) is almost twice as soluble as \(\ce{N_2}\). Although London dispersion forces are too weak to explain such a large difference, \(\ce{O_2}\) is paramagnetic and hence more polarizable than \(\ce{N_2}\), which explains its high solubility.

Table \(\PageIndex{1}\): Henry’s Law Constants for Selected Gases in Water at 20°C
Gas	Henry’s Law Constant [mol/(L·atm)] × 10⁻⁴
\(\ce{Ar}\)	15
\(\ce{CO_2}\)	392
\(\ce{H_2}\)	8.1
\(\ce{He}\)	3.9
\(\ce{N_2}\)	7.1
\(\ce{Ne}\)	4.7
\(\ce{O_2}\)	14

Gases that react with the solvent do not obey Henry’s law

Gases that react chemically with water, such as \(\ce{HCl}\) and the other hydrogen halides, \(\ce{H_2S}\), and \(\ce{NH_3}\), do not obey Henry’s law; all of these gases are much more soluble than predicted by Henry’s law. For example, \(\ce{HCl}\) reacts with water to give \(\ce{H^{+}(aq)}\) and \(\ce{Cl^{-}(aq)}\), not dissolved \(\ce{HCl}\) molecules,

\[\ce{HCl(g) + H2O(l) \rightarrow H3O^{+}(aq) + Cl^{-}(aq)} \nonumber\]

The dissociation of \(\ce{HCl}\) into ions results in a much higher effective "solubility" than expected for a neutral molecule.

Jan 3, 2019, 5:36 PM

https://en.Wikipedia.org/wiki/Henry%...constants_Heff

https://www.sciencedirect.com/scienc...0469818690079X

https://www.atmos-chem-phys.net/15/4...-4399-2015.pdf

Henry’s law has important applications. For example, bubbles of \(\ce{CO_2}\) form as soon as a carbonated beverage is opened because the drink was bottled under \(\ce{CO_2}\) at a pressure greater than 1 atm. When the bottle is opened, the pressure of \(\ce{CO_2}\) above the solution drops rapidly, and some of the dissolved gas escapes from the solution as bubbles. Henry’s law also explains why scuba divers have to be careful to ascend to the surface slowly after a dive if they are breathing compressed air. At the higher pressures under water, more \(\ce{N_2}\) from the air dissolves in the diver’s internal fluids. If the diver ascends too quickly, the rapid pressure change causes small bubbles of \(\ce{N_2}\) to form throughout the body, a condition known as “the bends.” These bubbles can block the flow of blood through the small blood vessels, causing great pain and even proving fatal in some cases.

Due to the low Henry’s law constant for \(\ce{O_2}\) in water, the levels of dissolved oxygen in water are too low to support the energy needs of multicellular organisms, including humans. To increase the \(\ce{O_2}\) concentration in internal fluids, organisms synthesize highly soluble carrier molecules that bind \(\ce{O_2}\) reversibly. For example, human red blood cells contain a protein called hemoglobin that specifically binds \(\ce{O_2}\) and facilitates its transport from the lungs to the tissues, where it is used to oxidize food molecules to provide energy. The concentration of hemoglobin in normal blood is about 2.2 mM, and each hemoglobin molecule can bind four \(\ce{O_2}\) molecules. Although the concentration of dissolved \(\ce{O_2}\) in blood serum at 37°C (normal body temperature) is only 0.010 mM, the total dissolved \(\ce{O_2}\) concentration is 8.8 mM, almost a thousand times greater than would be possible without hemoglobin. Synthetic oxygen carriers based on fluorinated alkanes have been developed for use as an emergency replacement for whole blood. Unlike donated blood, these “blood substitutes” do not require refrigeration and have a long shelf life. Their very high Henry’s law constants for \(\ce{O_2}\) result in dissolved oxygen concentrations comparable to those in normal blood.

Example \(\PageIndex{1}\): Oxygen in Water

The Henry’s law constant for \(\ce{O_2}\) in water at 25°C is \(1.27 \times 10^{-3} M/atm\), and the mole fraction of \(\ce{O_2}\) in the atmosphere is 0.21. Calculate the solubility of \(\ce{O_2}\) in water at 25°C at an atmospheric pressure of 1.00 atm.

Given: Henry’s law constant, mole fraction of \(\ce{O_2}\), and pressure

Asked for: solubility

Strategy:

Use Dalton’s law of partial pressures to calculate the partial pressure of oxygen.
Use Henry’s law (Equation \(\ref{11.61}\)) to calculate the solubility, expressed as the concentration of dissolved gas.

Solution:

A According to Dalton’s law, the partial pressure of \(O_2\) is proportional to the mole fraction of \(O_2\):

\[P_A = \chi_A P_t = (0.21)(1.00\; atm) = 0.21\; atm \nonumber\]

B From Henry’s law, the concentration of dissolved oxygen under these conditions is

\[CO_2=k_H P_{O_2}=(1.27 \times 10^{-3}\; M/\cancel{atm}) (0.21\; \cancel{atm}) =2.7 \times 10^{-4}\; M \nonumber\]

Exercise \(\PageIndex{1}\): Carbon Dioxide in Water

To understand why soft drinks “fizz” and then go “flat” after being opened, calculate the concentration of dissolved \(CO_2\) in a soft drink:

bottled under a pressure of 5.0 atm of \(CO_2\)
in equilibrium with the normal partial pressure of \(CO_2\) in the atmosphere (approximately \(3 \times 10^{-4} \;atm\)). The Henry’s law constant for \(CO_2\) in water at 25°C is \(3.4 \times 10^{-2}\; M/atm\).

Answer a: 0.17 M
Answer b: \(1 \times 10^{-5} M\)

Summary

The solubility of most substances depends strongly on the temperature and, in the case of gases, on the pressure. The solubility of most solid or liquid solutes increases with increasing temperature. The components of a mixture can often be separated using fractional crystallization, which separates compounds according to their solubilities. The solubility of a gas decreases with increasing temperature. Henry’s law describes the relationship between the pressure and the solubility of a gas.