17.6: Autoionization of Water and pH
- Last updated
- Save as PDF
- Page ID
- 392349
Learning Objectives
- To understand the autoionization reaction of liquid water.
- To know the relationship among pH, pOH, and \(pK_w\).
As you learned previously acids and bases can be defined in several different ways (Table \(\PageIndex{1}\)). Recall that the Arrhenius definition of an acid is a substance that dissociates in water to produce \(H^+\) ions (protons), and an Arrhenius base is a substance that dissociates in water to produce \(OH^−\) (hydroxide) ions. According to this view, an acid–base reaction involves the reaction of a proton with a hydroxide ion to form water. Although Brønsted and Lowry defined an acid similarly to Arrhenius by describing an acid as any substance that can donate a proton, the Brønsted–Lowry definition of a base is much more general than the Arrhenius definition. In Brønsted–Lowry terms, a base is any substance that can accept a proton, so a base is not limited to just a hydroxide ion. This means that for every Brønsted–Lowry acid, there exists a corresponding conjugate base with one fewer proton. Consequently, all Brønsted–Lowry acid–base reactions actually involve two conjugate acid–base pairs and the transfer of a proton from one substance (the acid) to another (the base). In contrast, the Lewis definition of acids and bases, focuses on accepting or donating pairs of electrons rather than protons. A Lewis base is an electron-pair donor, and a Lewis acid is an electron-pair acceptor.
| Definition | Acids | Bases |
|---|---|---|
| Arrhenius | \(H^+\) donor | \(OH^−\) donor |
| Brønsted–Lowry | \(H^+\) donor | \(H^+\) acceptor |
| Lewis | electron-pair acceptor | electron-pair donor |
Because this chapter deals with acid–base equilibria in aqueous solution, our discussion will use primarily the Brønsted–Lowry definitions and nomenclature. Remember, however, that all three definitions are just different ways of looking at the same kind of reaction: a proton is an acid, and the hydroxide ion is a base—no matter which definition you use. In practice, chemists tend to use whichever definition is most helpful to make a particular point or understand a given system. If, for example, we refer to a base as having one or more lone pairs of electrons that can accept a proton, we are simply combining the Lewis and Brønsted–Lowry definitions to emphasize the characteristic properties of a base.
Acid–Base Properties of Water
Recall that because of its highly polar structure, liquid water can act as either an acid (by donating a proton to a base) or a base (by using a lone pair of electrons to accept a proton). For example, when a strong acid such as HCl dissolves in water, it dissociates into chloride ions (\(Cl^−\)) and protons (\(H^+\)). The proton, in turn, reacts with a water molecule to form the hydronium ion (\(H_3O^+\)):
\[\underset{acid}{HCl_{(aq)}} + \underset{base}{H_2O_{(l)}} \rightarrow \underset{acid}{H_3O^+_{(aq)}} + \underset{base}{Cl^-_{(aq)}} \label{16.3.1a} \]
In this reaction, \(HCl\) is the acid, and water acts as a base by accepting an \(H^+\) ion. The reaction in Equation \ref{16.3.1a} is often written in a simpler form by removing \(H_2O\) from each side:
\[ HCl_{(aq)} \rightarrow H^+_{(aq)} + Cl^-_{(aq)} \label{16.3.1b} \]
In Equation \ref{16.3.1b}, the hydronium ion is represented by \(H^+\), although free \(H^+\) ions do not exist in liquid water as this reaction demonstrates:
\[ H^+_{(aq)} + H_2O_{(l)} \rightarrow H_3O^+_{(aq)} \nonumber \]
Water can also act as an acid, as shown in Equation \ref{16.3.2}. In this equilibrium reaction, \(H_2O\) donates a proton to \(NH_3\), which acts as a base:
\[\underset{acid}{H_2O_{(l)}} + \underset{base}{NH_{3(aq)}} \rightleftharpoons \underset{acid}{NH^+_{4 (aq)}} + \underset{base}{OH^-_{(aq)}} \label{16.3.2} \]
Water is thus termed amphiprotic, meaning that it can behave as either an acid or a base, depending on the nature of the other reactant. Notice that Equation \(\ref{16.3.2}\) is an equilibrium reaction as indicated by the double arrow and hence has an equilibrium constant associated with it.
The Ion-Product Constant of Liquid Water
Because water is amphiprotic, one water molecule can react with another to form an \(OH^−\) ion and an \(H_3O^+\) ion in an autoionization process:
\[2H_2O_{(l)} \rightleftharpoons H_3O^+_{(aq)}+OH^−_{(aq)} \label{16.3.3} \]
The equilibrium constant \(K\) for this reaction can be written as follows:
\[K_{a}=\dfrac{a_{H_3O^+}·a_{OH^-}}{a_{H_2O}^2} \approx \frac{[H_{3}O^{+}][HO^{-}]}{(1)^{2}}=[H_{3}O^{+}][HO^{-}] \label{16.3.4} \]
where \(a\) is the activity of a species. Because water is the solvent, and the solution is assumed to be dilute, the activity of the water is approximated by the activity of pure water, which is defined as having a value of 1. The activity of each solute is approximated by the molarity of the solute.
Note
It is a common error to claim that the molar concentration of the solvent is in some way involved in the equilibrium law. This error is a result of a misunderstanding of solution thermodynamics. For example, it is often claimed that Ka = Keq[H2O] for aqueous solutions. This equation is incorrect because it is an erroneous interpretation of the correct equation Ka = Keq(\(\textit{a}_{H_2O}\)). Because \(\textit{a}_{H_2O}\) = 1 for a dilute solution, Ka = Keq(1), or Ka = Keq.
In this reaction, one water molecule acts as an acid and one water molecule acts as a base. Thus, this reaction actually can be designated as the \(K_a\) of water and as the \(K_b\) of water. It is most common, however, to designate this reaction and the associated law of mass action as the \(K_w\) of water:
\[K_{w}=[H_{3}O^{+}][HO^{-}] \label{16.3.5} \]
When pure liquid water is in equilibrium with hydronium and hydroxide ions at 25 °C, the concentrations of the hydronium ion and the hydroxide ion are equal:
\[[H_3O^+] = [OH^−] = 1.003 \times 10^{−7}\; M \label{16.3.6} \]
Thus the number of dissociated water molecules is very small indeed, approximately 2 ppb.
Substituting the values for \([H_3O^+]\) and \([OH^−]\) at 25 °C into this expression
\[K_w=(1.003 \times10^{−7})(1.003 \times 10^{−7})=1.006 \times 10^{−14} \label{16.3.7} \]
Thus, to three significant figures, \(K_w = 1.01 \times 10^{−14}\) at room temperature, and \[K_w = 1.01 \times 10^{-14} = [H_3O^+][OH^-] \label{16.3.7b} \].
Like any other equilibrium constant, \(K_w\) varies with temperature, ranging from \(1.15 \times 10^{−15}\) at 0 °C to \(4.99 \times 10^{−13}\) at 100 °C.
In pure water, the concentrations of the hydronium ion and the hydroxide ion are equal, and the solution is therefore neutral. If \([H_3O^+] > [OH^−]\), however, the solution is acidic, whereas if \([H_3O^+] < [OH^−]\), the solution is basic. For an aqueous solution, the \(H_3O^+\) concentration is a quantitative measure of acidity: the higher the \(H_3O^+\) concentration, the more acidic the solution. Conversely, the higher the \(OH^−\) concentration, the more basic the solution. In most situations that you will encounter, the \(H_3O^+\) and \(OH^−\) concentrations from the dissociation of water are so small (\(1.003 \times 10^{−7} M\)) that they can be ignored in calculating the \(H_3O^+\) or \(OH^−\) concentrations of solutions of acids and bases, but this is not always the case.
A Video Describing the Self-Ionization of Water (Kw): Self-Ionization of Water (Kw): [youtu.be]
The Relationship among pH, pOH, and \(pK_w\)
The pH scale is a concise way of describing the \(H_3O^+\) concentration and hence the acidity or basicity of a solution. Recall that pH and the \(H^+\) (\(H_3O^+\)) concentration are related as follows:
\[pH=−\log_{10}[H^+] \label{16.3.8} \]
\[[H^+]=10^{−pH} \label{16.3.9} \]
Because the scale is logarithmic, a pH difference of 1 between two solutions corresponds to a difference of a factor of 10 in their hydronium ion concentrations. Recall also that the pH of a neutral solution is 7.00 (\([H_3O^+] = 1.0 \times 10^{−7}\; M\)), whereas acidic solutions have pH < 7.00 (corresponding to \([H_3O^+] > 1.0 \times 10^{−7}\)) and basic solutions have pH > 7.00 (corresponding to \([H_3O^+] < 1.0 \times 10^{−7}\)).
Similar notation systems are used to describe many other chemical quantities that contain a large negative exponent. For example, chemists use an analogous pOH scale to describe the hydroxide ion concentration of a solution. The pOH and \([OH^−]\) are related as follows:
\[pOH=−\log_{10}[OH^−] \label{16.3.10} \]
\[[OH^−]=10^{−pOH} \label{16.3.11} \]
The constant \(K_w\) can also be expressed using this notation, where \(pK_w = −\log\; K_w\).
Because a neutral solution has \([OH^−] = 1.0 \times 10^{−7}\), the pOH of a neutral solution is 7.00. Consequently, the sum of the pH and the pOH for a neutral solution at 25 °C is 7.00 + 7.00 = 14.00. We can show that the sum of pH and pOH is equal to 14.00 for any aqueous solution at 25 °C by taking the negative logarithm of both sides of Equation \ref{16.3.6b}:
\[\begin{align} −\log_{10} K_w &= pK_w \\[4pt] &=−\log([H_3O^{+}][OH^{−}]) \\[4pt] &= (−\log[H_3O^{+}])+(−\log[OH^{−}])\\[4pt] &= pH+pOH \label{16.3.12} \end{align} \]
Thus at any temperature, \(pH + pOH = pK_w\), so at 25 °C, where \(K_w = 1.0 \times 10^{−14}\), pH + pOH = 14.00. More generally, the pH of any neutral solution is half of the \(pK_w\) at that temperature. The relationship among pH, pOH, and the acidity or basicity of a solution is summarized graphically in Figure \(\PageIndex{1}\) over the common pH range of 0 to 14. Notice the inverse relationship between the pH and pOH scales.
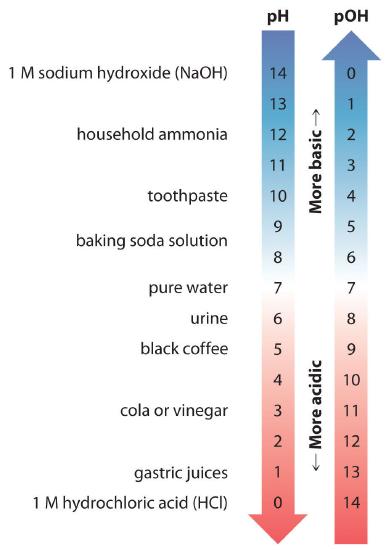
For any neutral solution, pH + pOH = 14.00 (at 25 °C) with pH=pOH=7.
A Video Introduction to pH: Introduction to pH [youtu.be]
Example \(\PageIndex{1}\)
The Kw for water at 100 °C is \(4.99 \times 10^{−13}\). Calculate \(pK_w\) for water at this temperature and the pH and the pOH for a neutral aqueous solution at 100 °C. Report pH and pOH values to two decimal places.
Given: \(K_w\)
Asked for: \(pK_w\), \(pH\), and \(pOH\)
Strategy:
- Calculate \(pK_w\) by taking the negative logarithm of \(K_w\).
- For a neutral aqueous solution, \([H_3O^+] = [OH^−]\). Use this relationship and Equation \ref{16.3.7b} to calculate \([H_3O^+]\) and \([OH^−]\). Then determine the pH and the pOH for the solution.
Solution:
A
Because \(pK_w\) is the negative logarithm of Kw, we can write
\[pK_w = −\log K_w = −\log(4.99 \times 10^{−13}) = 12.302 \nonumber \]
The answer is reasonable: \(K_w\) is between \(10^{−13}\) and \(10^{−12}\), so \(pK_w\) must be between 12 and 13.
B
Equation \ref{16.3.6b} shows that \(K_w = [H_3O^+][OH^−]\). Because \([H_3O^+] = [OH^−]\) in a neutral solution, we can let \(x = [H_3O^+] = [OH^−]\):
\[\begin{align*} K_w &=[H_3O^+][OH^−] \\[4pt] &=(x)(x)=x^2 \\[4pt] x&=\sqrt{K_w} \\[4pt] &=\sqrt{4.99 \times 10^{−13}} \\[4pt] &=7.06 \times 10^{−7}\; M \end{align*} \nonumber \]
Because \(x\) is equal to both \([H_3O^+]\) and \([OH^−]\),
\[\begin{align*} pH &= pOH = −\log(7.06 \times 10^{−7}) \\[4pt] &= 6.15 \,\,\, \text{(to two decimal places)} \end{align*} \nonumber \]
We could obtain the same answer more easily (without using logarithms) by using the \(pK_w\). In this case, we know that \(pK_w = 12.302\), and from Equation \ref{16.3.12}, we know that \(pK_w = pH + pOH\). Because \(pH = pOH\) in a neutral solution, we can use Equation \ref{16.3.12} directly, setting \(pH = pOH = y\). Solving to two decimal places we obtain the following:
\[\begin{align*} pK_w &= pH + pOH \\[4pt] &= y + y \\[4pt] &= 2y \\[4pt] y &=\dfrac{pK_w}{2} \\[4pt] &=\dfrac{12.302}{2} \\[4pt] &=6.15 =pH=pOH \end{align*} \nonumber \]
Exercise \(\PageIndex{1}\)
Humans maintain an internal temperature of about 37 °C. At this temperature, \(K_w = 3.55 \times 10^{−14}\). Calculate \(pK_w\) and the pH and the pOH of a neutral solution at 37 °C. Report pH and pOH values to two decimal places.
- Answer
-
- \(pK_w = 13.45\)
- \(pH = pOH = 6.73\)
Summary
Water is amphiprotic: it can act as an acid by donating a proton to a base to form the hydroxide ion, or as a base by accepting a proton from an acid to form the hydronium ion (\(H_3O^+\)). The autoionization of liquid water produces \(OH^−\) and \(H_3O^+\) ions. The equilibrium constant for this reaction is called the ion-product constant of liquid water (Kw) and is defined as \(K_w = [H_3O^+][OH^−]\). At 25 °C, \(K_w\) is \(1.01 \times 10^{−14}\); hence \(pH + pOH = pK_w = 14.00\).
- For any neutral solution, \(pH + pOH = 14.00\) (at 25 °C) and \(pH = 1/2 pK_w\).
- Ion-product constant of liquid water: \[K_w = [H_3O^+][OH^−] \nonumber \]
- Definition of \(pH\): \[pH = −\log10[H^+] \nonumber \] or \[[H^+] = 10^{−pH} \nonumber \]
- Definition of \(pOH\): \[pOH = −\log_{10}[OH^+] \nonumber \] or \[[OH^−] = 10^{−pOH} \nonumber \]
- Relationship among \(pH\), \(pOH\), and \(pK_w\): \[pK_w= pH + pOH \nonumber \]

