3.4: The Wavelength Nature of Matter
- Page ID
- 28978
- To understand the wave–particle duality of matter.
Einstein’s photons of light were individual packets of energy having many of the characteristics of particles. Recall that the collision of an electron (a particle) with a sufficiently energetic photon can eject a photoelectron from the surface of a metal. Any excess energy is transferred to the electron and is converted to the kinetic energy of the ejected electron. Einstein’s hypothesis that energy is concentrated in localized bundles, however, was in sharp contrast to the classical notion that energy is spread out uniformly in a wave. Light exhibits a wave-particle duality and may described as either a particle or a wave depending on the experiment.
Diffraction is a Wave Phenomenon
It is well-known that light has the ability to diffract around objects in its path, leading to an interference pattern that is particular to the object. This is, in fact, how holography works (the interference pattern is created by allowing the diffracted light to interfere with the original beam so that the hologram can be viewed by shining the original beam on the image). A simple illustration of light diffraction is the Young double slit experiment (Figure \(\PageIndex{1}\)).

Here, we use light pictured as waves in a plane parallel to the double slit apparatus and observe what happens when they impinge on the slits. Each slit becomes a point source for spherical waves that subsequently interfere with each other, giving rise to the light and dark fringes on the screen at the right. Interference is a wave phenomenon in which two waves superimpose to form a resultant wave of greater or lower amplitude. It is a primary property used to identify wave behavior in nature.
According to classical physics, electrons should behave like particles - they travel in straight lines and do not curve in flight unless acted on by an external agent, like a magnetic field. In this model, if we fire a beam of electrons through a double slit onto a detector, we should get two bands of "hits", much as you would get if you fired a machine gun at the side of a house with two windows - you would get two areas of bullet-marked wall inside, and the rest would be intact Figure \(\PageIndex{2; left}\). However, if the slits are made small enough and close enough together, experimentalist actually observe the electrons diffracting through the slits and interfering with each other just like light waves (Figure \(\PageIndex{2; right}\)). This means that the electrons exhibit a similar wave-particle duality that light exhibits. In this case, they must have properties like wavelength and frequency. We can deduce the properties from the behavior of the electrons as they pass through our diffraction grating.


The observation that particles may exhibit wavelength phenomena was a pivotal result in the development of quantum mechanics. For physicists this idea was important because it meant that not only could any particle exhibit wave characteristics, but that one could use wave equations to describe phenomena in matter. In his PhD dissertation submitted to the Sorbonne in 1924, Louis de Broglie (1892–1972) proposed that a particle such as an electron could be described by a wave whose wavelength is given by
\[\lambda =\dfrac{h}{mv} \label{6.4.3}\]
where
- \(\lambda\) is the de Broglie wavelength,
- \(h\) is Planck’s constant,
- \(m\) is the mass of the particle, and
- \(v\) is the velocity of the particle.
It turned out that de Broglie hypothesis was able to accurately describe a range of diffraction phenomena of matter. For his work, de Broglie received the Nobel Prize in Physics in 1929.
If particles exhibit the properties of waves, why had no one observed them before? The answer lies in the numerator of de Broglie’s equation (Equation \ref{6.4.3}, which is an extremely small number. As you will calculate in Example \(\PageIndex{1}\), Planck’s constant (6.63 × 10−34 J•s) is so small that the wavelength of a particle with a large mass is simply too short (less than the diameter of an atomic nucleus) to be noticeable.
Calculate the wavelength of a baseball, which has a mass of 149 g and a speed of 100 mi/h.
Given: mass and speed of object
Asked for: wavelength
Strategy:
- Convert the speed of the baseball to the appropriate SI units: meters per second.
- Substitute values into Equation \(\ref{6.4.3}\) and solve for the wavelength.
Solution:
The wavelength of a particle is given by \(λ = h/mv\). We know that m = 0.149 kg, so all we need to find is the speed of the baseball:
\( v=\left ( \dfrac{100\; \cancel{mi}}{\cancel{h}} \right )\left ( \dfrac{1\; \cancel{h}}{60\; \cancel{min}} \right )\left ( \dfrac{1.609\; \cancel{km}}{\cancel{mi}} \right )\left ( \dfrac{1000\; m}{\cancel{km}} \right ) \)
B Recall that the joule is a derived unit, whose units are (kg•m2)/s2. Thus the wavelength of the baseball is
\[\begin{align*} \lambda &=\dfrac{6.626\times 10^{-34}\; J\cdot s}{\left ( 0.149\; kg \right )\left ( 44.69\; m\cdot s \right )} \\[4pt] &= \dfrac{6.626\times 10^{-34}\; \cancel{kg}\cdot m{^\cancel{2}\cdot \cancel{s}{\cancel{^{-2}}\cdot \cancel{s}}}}{\left ( 0.149\; \cancel{kg} \right )\left ( 44.69\; \cancel{m}\cdot \cancel{s^{-1}} \right )} \\[4pt] &=9.95\times 10^{-35}\; m \end{align*}\]
(You should verify that the units cancel to give the wavelength in meters.) Given that the diameter of the nucleus of an atom is approximately 10−14 m, the wavelength of the baseball is almost unimaginably small.
Calculate the wavelength of a neutron that is moving at 3.00 × 103 m/s.
- Answer
-
1.32 Å, or 132 pm
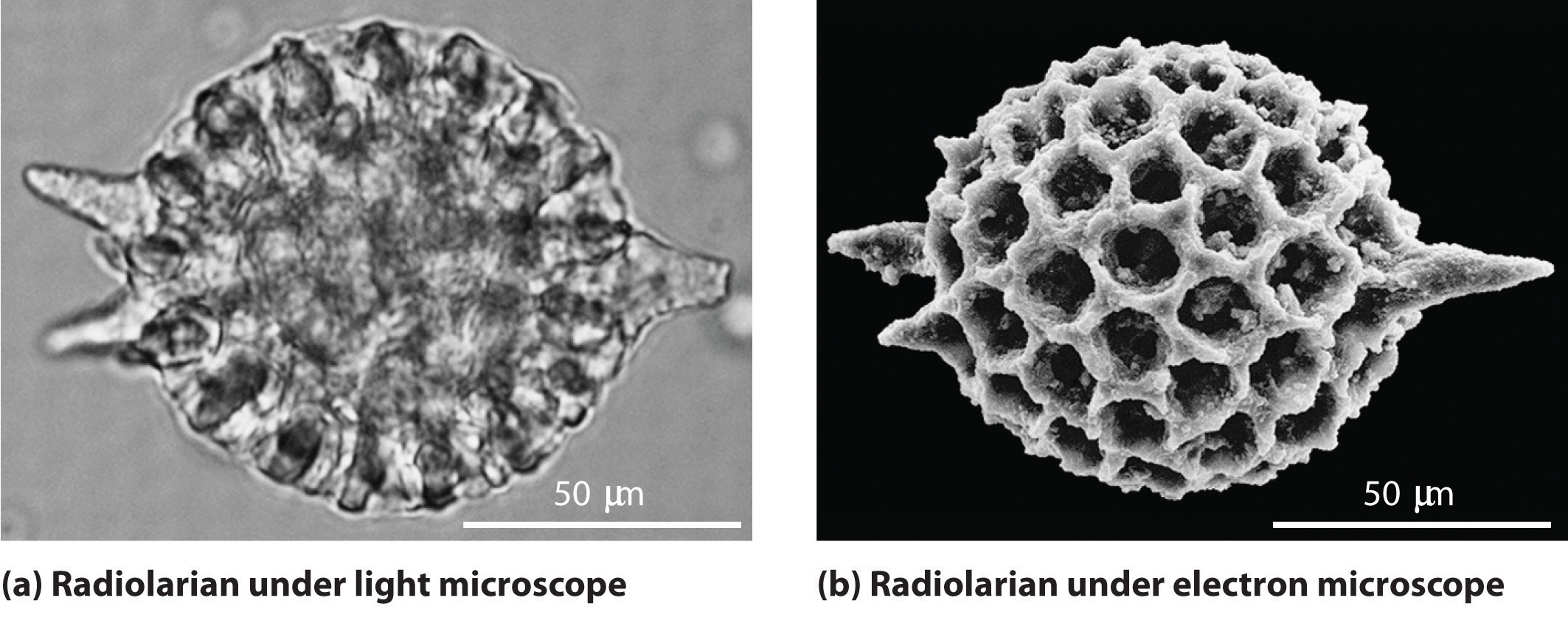
As you calculated in Example \(\PageIndex{1}\), objects such as a baseball or a neutron have such short wavelengths that they are best regarded primarily as particles. In contrast, objects with very small masses (such as photons) have large wavelengths and can be viewed primarily as waves. Objects with intermediate masses, however, such as electrons, exhibit the properties of both particles and waves. Although we still usually think of electrons as particles, the wave nature of electrons is employed in an electron microscope, which has revealed most of what we know about the microscopic structure of living organisms and materials. Because the wavelength of an electron beam is much shorter than the wavelength of a beam of visible light, this instrument can resolve smaller details than a light microscope can (Figure \(\PageIndex{3}\)).
The Heisenberg Uncertainty Principle
Because a wave is a disturbance that travels in space, it has no fixed position. One might therefore expect that it would also be hard to specify the exact position of a particle that exhibits wavelike behavior. Hence, an "uncertainty principle" for light is merely a conclusion about the nature of electromagnetic waves and nothing new. De Broglie's idea of wave-particle duality means that particles such as electrons which exhibit an uncertainty principle. This was described mathematically by the German physicist Werner Heisenberg (1901–1976; Nobel Prize in Physics, 1932), who related the position of a particle to its momentum. Referring to the electron, Heisenberg stated that “at every moment the electron has only an inaccurate position and an inaccurate velocity, and between these two inaccuracies there is this uncertainty relation.” Mathematically, the Heisenberg uncertainty principle states that the uncertainty in the position of a particle (\(Δx\)) multiplied by the uncertainty in its momentum [\(Δ(mv)\)] is greater than or equal to Planck’s constant divided by \(4π\):
\[ \left ( \Delta x \right )\left ( \Delta \left [ mv \right ] \right )\ge \dfrac{h}{4\pi } \label{6.4.7} \]
Because Planck’s constant is a very small number, the Heisenberg uncertainty principle is important only for particles such as electrons that have very low masses. These are the same particles predicted by de Broglie’s equation to have measurable wavelengths.
If the precise position \(x\) of a particle is known absolutely (\(Δx = 0\)), then the uncertainty in its momentum must be infinite:
\[ \left ( \Delta \left [ mv \right ] \right )= \dfrac{h}{4\pi \left ( \Delta x \right ) }=\dfrac{h}{4\pi \left ( 0 \right ) }=\infty \label{6.4.8} \]
Because the mass of the electron at rest (\(m\)) is both constant and accurately known, the uncertainty in \(Δ(mv)\) must be due to the \(Δv\) term, which would have to be infinitely large for \(Δ(mv)\) to equal infinity. That is, according to Equation \(\ref{6.4.8}\), the more accurately we know the exact position of the electron (as \(Δx → 0\)), the less accurately we know the speed and the kinetic energy of the electron (1/2 mv2) because \(Δ(mv) → ∞\). Conversely, the more accurately we know the precise momentum (and the energy) of the electron [as \(Δ(mv) → 0\)], then \(Δx → ∞\) and we have no idea where the electron is.
Determine the minimum uncertainties in the positions of the following objects if their speeds are known with a precision of \(1.0 \times 10^{-3} m/s\):
- an electron and
- a bowling ball of mass 6.0 kg.
Strategy
Given the uncertainty in speed \(\Delta u = 1.0 \times 10^{-3} m/s\), we have to first determine the uncertainty in momentum \(\Delta p = m\Delta u\) and then invert Equation \ref{Heisen} to find the uncertainty in position
\[\Delta x = \dfrac{\hbar}{2\Delta p}. \nonumber\]
Solution
- For the electron: \[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (9.1 \times 10^{-31} kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 9.1 \times 10^{-34} kg \cdot m/s,\end{align*} \] \[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 5.8 \, cm. \end{align*} \]
- For the bowling ball: \[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (6.0 \, kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 6.0 \times 10^{-3} kg \cdot m/s, \end{align*}\] \[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 8.8 \times 10^{-33}m. \end{align*} \]
Significance
Unlike the position uncertainty for the electron, the position uncertainty for the bowling ball is immeasurably small. Planck’s constant is very small, so the limitations imposed by the uncertainty principle are not noticeable in macroscopic systems such as a bowling ball.
Indeterminacy and Probability Distribution Maps
Before either quantum mechanics, physicists described the world using "Classical Mechanics," which is like what you've probably studied before in physics class: Newtonian mechanics (forces, accelerations, etc), electricity and magnetism using Maxwell's equations. All these approaches work well for big things that are not moving too fast. There are two qualities of classical mechanics that quantum mechanics altered. First, in classical mechanics energy and velocity and such quantities can have any value. If you drop a ball, it accelerates smoothly from 0 to a final velocity, rather than moving jerkily from step to step. The Quantum Mechanics got rid of the assumptions that energy and velocity should be "continuous."
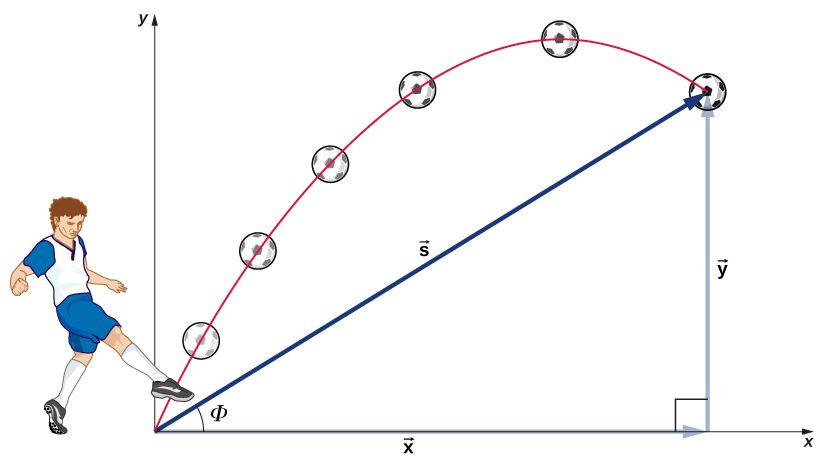
A trajectory is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a complete trajectory is defined by knowledge of position and momentum, simultaneously. If you launch a missile, a space shuttle or kick a ball (Figure \(\PageIndex{1}\)), you can calculate almost exactly the path it will follow; if you have perfect knowledge of the forces acting on it, you can calculate its path perfectly. This is because Newton's laws are completely deterministic - that is because they imply that anything that happens at any future time is completed determined by what happens now, and moreover that everything now was completely determined by what happened at any time in the past.
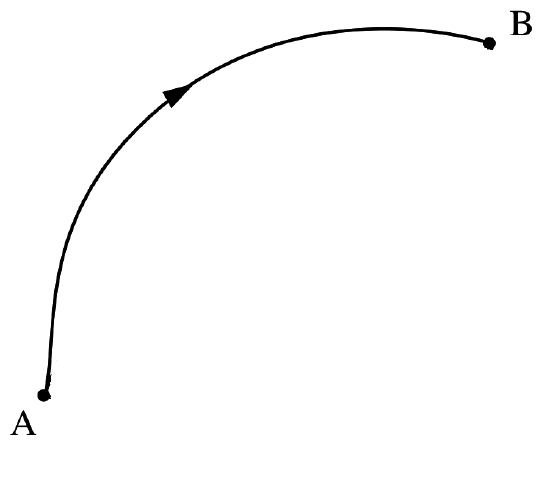
However, as discussed above, due to Heisenberg uncertainty principle, position and momentum cannot be measured simultaneously. This means the concept of a trajectory in quantum mechanics is not defined and we actually do not know where they are or what path they follow (Figure \(\PageIndex{4}\)). Quantum mechanics is a probabilitic theory, that discards the concept of trajectory for small particles, and uses statistics and probability to describe evolution.

Summary
An electron possesses both particle and wave properties. The modern model for the electronic structure of the atom is based on recognizing that an electron possesses particle and wave properties, the so-called wave–particle duality. Louis de Broglie showed that the wavelength of a particle is equal to Planck’s constant divided by the mass times the velocity of the particle.
\[\lambda =\dfrac{h}{mv} \nonumber \]
The electron in Bohr’s circular orbits could thus be described as a standing wave, one that does not move through space. Standing waves are familiar from music: the lowest-energy standing wave is the fundamental vibration, and higher-energy vibrations are overtones and have successively more nodes, points where the amplitude of the wave is always zero. Werner Heisenberg’s uncertainty principle states that it is impossible to precisely describe both the location and the speed of particles that exhibit wavelike behavior.
\[ \left ( \Delta x \right )\left ( \Delta \left [ mv \right ] \right )\geqslant \dfrac{h}{4\pi } \nonumber\]
Contributors and Attributions
Modified by Joshua Halpern (Howard University)
Emily V Eames (City College of San Francisco)
- OpenStax Physics

