21.5: Lattice Energies of Crystals
- Page ID
- 41666
- To understand the relationship between the lattice energy and physical properties of an ionic compound.
- To use the Born–Haber cycle to calculate lattice energies.
Recall that the reaction of a metal with a nonmetal usually produces an ionic compound; that is, electrons are transferred from the metal (the reductant) to the nonmetal (the oxidant). Ionic compounds are usually rigid, brittle, crystalline substances with flat surfaces that intersect at characteristic angles. They are not easily deformed, and they melt at relatively high temperatures. \(\ce{NaCl}\), for example, melts at 801°C. These properties result from the regular arrangement of the ions in the crystalline lattice and from the strong electrostatic attractive forces between ions with opposite charges.
While formation of ion pairs from isolated ions releases large amounts of energy, even more energy is released when these ion pairs condense to form an ordered three-dimensional array. In such an arrangement each cation in the lattice is surrounded by more than one anion (typically four, six, or eight) and vice versa, so it is more stable than a system consisting of separate pairs of ions, in which there is only one cation–anion interaction in each pair. Note that \(r_0\) may differ between the gas-phase dimer and the lattice.
An ionic lattice is more stable than a system consisting of separate ion pairs.
Calculating (Ionic) Lattice Energies
The lattice energy of nearly any ionic solid can be calculated rather accurately using a modified form of Coulomb's law:
\[U=−\dfrac{k′Q_1Q_2}{r_0} \label{21.5.1} \]
where \(U\), which is always a positive number, represents the amount of energy required to dissociate 1 mol of an ionic solid into the gaseous ions. The proportionality constant in Equation \(\ref{21.5.1}\) is expanded below, but it is worthwhile to discuss its general features first.
If we assume that \(ΔV = 0\), then the lattice energy, \(U\), is approximately equal to the change in enthalpy, \(ΔH\):
\[\ce{MX(s) \rightarrow M^{+n} (g) + X^{−n} (g)} \quad \quad ΔH \approx U \label{21.5.2} \]
As before, \(Q_1\) and \(Q_2\) are the charges on the ions and \(r_0\) is the internuclear distance. We see from Equation \(\ref{21.5.1}\) that lattice energy is directly related to the product of the ion charges and inversely related to the internuclear distance. The value of the constant \(k′\) depends on the specific arrangement of ions in the solid lattice and their valence electron configurations. Representative values for calculated lattice energies, which range from about 600 to 10,000 kJ/mol, are listed in Table \(\PageIndex{1}\). Energies of this magnitude can be decisive in determining the chemistry of the elements.
| Substance | U (kJ/mol) |
|---|---|
| NaI | 682 |
| CaI2 | 1971 |
| MgI2 | 2293 |
| NaOH | 887 |
| Na2O | 2481 |
| NaNO3 | 755 |
| Ca3(PO4)2 | 10,602 |
| CaCO3 | 2804 |
|
Source: Data from CRC Handbook of Chemistry and Physics (2004).
|
|
Because the lattice energy depends on the product of the charges of the ions, a salt having a metal cation with a +2 charge (M2+) and a nonmetal anion with a −2 charge (X2−) will have a lattice energy four times greater than one with \(\ce{M^{+}}\) and \(\ce{X^{−}}\), assuming the ions are of comparable size (and have similar internuclear distances). For example, the calculated value of \(U\) for \(\ce{NaF}\) is 910 kJ/mol, whereas \(U\) for \(\ce{MgO}\) (containing \(\ce{Mg^{2+}}\) and \(\ce{O^{2−}}\) ions) is 3795 kJ/mol.
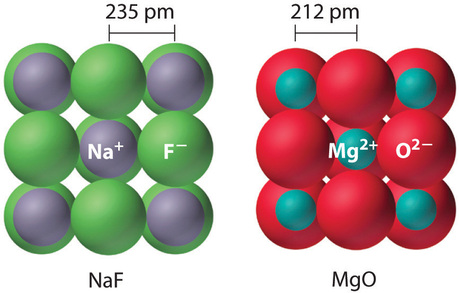
Because lattice energy is inversely related to the internuclear distance, it is also inversely proportional to the size of the ions. This effect is illustrated in Figure \(\PageIndex{1}\), which shows that lattice energy decreases for the series \(\ce{LiX}\), \(\ce{NaX}\), and \(\ce{KX}\) as the radius of \(\ce{X^{−}}\) increases. Because \(r_0\) in Equation \(\ref{21.5.1}\) is the sum of the ionic radii of the cation and the anion (r0 = r+ + r−), r0 increases as the cation becomes larger in the series, so the magnitude of U decreases. A similar effect is seen when the anion becomes larger in a series of compounds with the same cation.
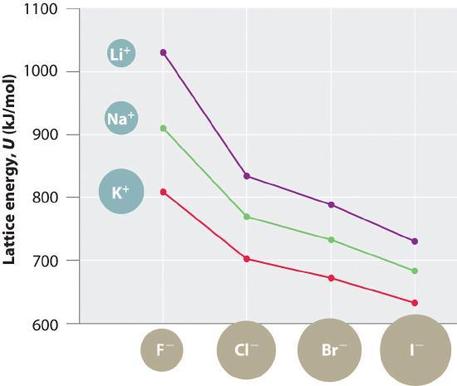
Because the ionic radii of the cations decrease in the order \(\ce{K^{+} > Na^{+} > Li^{+}}\) for a given halide ion, the lattice energy decreases smoothly from \(\ce{Li^{+}}\) to \(\ce{K^{+}}\). Conversely, for a given alkali metal ion, the fluoride salt always has the highest lattice energy and the iodide salt the lowest.
Lattice energies are highest for substances with small, highly charged ions.
Arrange GaP, BaS, CaO, and RbCl in order of increasing lattice energy.
Given: four compounds
Asked for: order of increasing lattice energy
Strategy:
Using Equation \(\ref{21.5.1}\), predict the order of the lattice energies based on the charges on the ions. For compounds with ions with the same charge, use the relative sizes of the ions to make this prediction.
Solution:
The compound GaP, which is used in semiconductor electronics, contains Ga3+ and P3− ions; the compound BaS contains Ba2+ and S2− ions; the compound CaO contains Ca2+ and O2− ions; and the compound RbCl has Rb+ and Cl− ions. We know from Equation \(\ref{21.5.1}\) that lattice energy is directly proportional to the product of the ionic charges. Consequently, we expect RbCl, with a (−1)(+1) term in the numerator, to have the lowest lattice energy, and GaP, with a (+3)(−3) term, the highest. To decide whether BaS or CaO has the greater lattice energy, we need to consider the relative sizes of the ions because both compounds contain a +2 metal ion and a −2 chalcogenide ion. Because Ba2+ lies below Ca2+ in the periodic table, Ba2+ is larger than Ca2+. Similarly, S2− is larger than O2−. Because the cation and the anion in BaS are both larger than the corresponding ions in CaO, the internuclear distance is greater in BaS and its lattice energy will be lower than that of CaO. The order of increasing lattice energy is RbCl < BaS < CaO < GaP.
Arrange InAs, KBr, LiCl, SrSe, and ZnS in order of decreasing lattice energy.
- Answer
-
InAs > ZnS > SrSe > LiCl > KBr
Lattice Energy also Depends on Crystal Structure
There are many other factors to be considered such as covalent character and electron-electron interactions in ionic solids. But for simplicity, let us consider the ionic solids as a collection of positive and negative ions. In this simple view, appropriate number of cations and anions come together to form a solid. The positive ions experience both attraction and repulsion from ions of opposite charge and ions of the same charge.
As an example, let us consider the the \(\ce{NaCl}\) crystal. In the following discussion, assume r be the distance between Na+ and Cl- ions. The nearest neighbors of Na+ are 6 Cl- ions at a distance 1r, 12 Na+ ions at a distance 2r, 8 Cl- at 3r, 6 Na+ at 4r, 24 Na+ at 5r, and so on. Thus, the electrostatic potential of a single ion in a crystal by approximating the ions by point charges of the surrounding ions:
\[ E_{ion-lattice} = \dfrac{Z^2e^2}{4\pi\epsilon_or} M \label{12.5.4} \]
The Madelung constant \(M\) - named after Erwin Medelung - is a geometrical factor that depends on the arrangement of ions in the solid. For example, \(M\) for \(\ce{NaCl}\) is a poorly converging series of interaction energies:
\[ M= \dfrac{6}{1} - \dfrac{12}{2} + \dfrac{8}{3} - \dfrac{6}{4} + \dfrac{24}{5} ... \label{21.5.5} \]
with
- \(Z\) is the number of charges of the ions, (e.g., 1 for \(\ce{NaCl}\) ),
- \(e\) is the charge of an electron (\(1.6022 \times 10^{-19}\; C\)),
- \(4\pi \epsilon_o\) is 1.11265x10-10 C2/(J m).
The Madelung constant depends on the structure type and Equation \(\ref{21.5.5}\) is applicable only for the sodium chloride (e.g., rock salt) lattice geometry. Other values for other structural types are given in Table \(\PageIndex{2}\).
|
|
|
|
A : C | Type |
|---|---|---|---|---|
| NaCl | NaCl | 1.74756 | 6 : 6 | Rock salt |
| CsCl | CsCl | 1.76267 | 6 : 6 | CsCl type |
| CaF2 | Cubic | 2.51939 | 8 : 4 | Fluorite |
| CdCl2 | Hexagonal | 2.244 | ||
| MgF2 | Tetragonal | 2.381 | ||
| ZnS (wurtzite) | Hexagonal | 1.64132 | ||
| TiO2 (rutile) | Tetragonal | 2.408 | 6 : 3 | Rutile |
| bSiO2 | Hexagonal | 2.2197 | ||
| Al2O3 | Rhombohedral | 4.1719 | 6 : 4 | Corundum |
There are other factors to consider for the evaluation of lattice energy and the treatment by Max Born and Alfred Landé led to the formula for the evaluation of lattice energy for a mole of crystalline solid. The Born–Landé equation (Equation \(\ref{21.5.6}\)) is a means of calculating the lattice energy of a crystalline ionic compound and derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term
\[ U= \dfrac{N_A M z^{+}z^{-} e^2}{4\pi \epsilon_o r_o} \left( 1 - \dfrac{1}{n} \right) \label{21.5.6} \]
where
- \(N_A\) is Avogadro constant
- \(M\) is the Madelung constant for the lattice
- \(z^{+}\) is the charge number of cation
- \(z^{−}\) is the charge number of anion
- \(e\) is elementary charge (\(1.6022×10^{−19} C\))
- \(ε_0\) is the permittivity of free space (\(8.854 \times 10^{-12} C^2/m\))
- \(r_0\) is the distance to closest ion
- \(n\) is the Born exponent that is typically between 5 and 12 and is determined experimentally. \(n\) is a number related to the electronic configurations of the ions involved (Table \(\PageIndex{3}\)).
| Atom/Molecule | n |
|---|---|
| He | 5 |
| Ne | 7 |
| Ar | 9 |
| Kr | 10 |
| Xe | 12 |
| LiF | 5.9 |
| LiCl | 8.0 |
| LiBr | 8.7 |
| NaCl | 9.1 |
| NaBr | 9.5 |
Estimate the lattice energy for \(\ce{NaCl.}\)
Solution
Using the values giving in the discussion above, the estimation is given by Equation \ref{21.5.6}
\[ \begin{align*}U_{NaCl} &= \dfrac{(6.022 \times 10^{23} /mol) (1.74756) (1)(1) (1.6022 \times 10 ^{-19}\,C)^2}{ 4\pi \, (8.854 \times 10^{-12} C^2/m ) (282 \times 10^{-12}\; m)} \left( 1 - \dfrac{1}{9.1} \right) \\[4pt] &= - 756\, kJ/mol \end{align*} \]
Discussion
Much more should be considered in order to evaluate the lattice energy accurately, but the above calculation leads you to a good start. When methods to evaluate the energy of crystallization or lattice energy lead to reliable values, these values can be used in the Born-Hable cycle to evaluate other chemical properties, for example the electron affinity, which is really difficult to determine directly by experiment.
The Relationship between Lattice Energies and Physical Properties
The magnitude of the forces that hold an ionic substance together has a dramatic effect on many of its properties. The melting point, for example, is the temperature at which the individual ions have enough kinetic energy to overcome the attractive forces that hold them in place. At the melting point, the ions can move freely, and the substance becomes a liquid. Thus melting points vary with lattice energies for ionic substances that have similar structures. The melting points of the sodium halides (Figure \(\PageIndex{2}\)), for example, decrease smoothly from NaF to NaI, following the same trend as seen for their lattice energies (Figure \(\PageIndex{1}\)). Similarly, the melting point of MgO is 2825°C, compared with 996°C for NaF, reflecting the higher lattice energies associated with higher charges on the ions. In fact, because of its high melting point, MgO is used as an electrical insulator in heating elements for electric stoves.
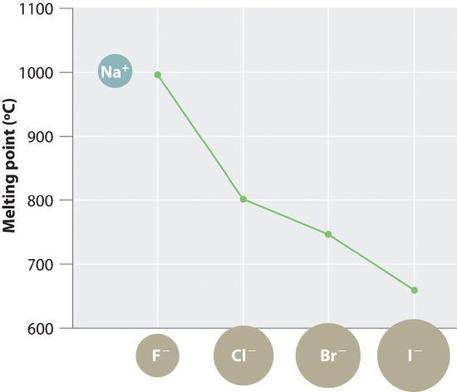
The hardness of ionic materials—that is, their resistance to scratching or abrasion—is also related to their lattice energies. Hardness is directly related to how tightly the ions are held together electrostatically, which, as we saw, is also reflected in the lattice energy. As an example, MgO is harder than NaF, which is consistent with its higher lattice energy.
In addition to determining melting point and hardness, lattice energies affect the solubilities of ionic substances in water. In general, the higher the lattice energy, the less soluble a compound is in water. For example, the solubility of NaF in water at 25°C is 4.13 g/100 mL, but under the same conditions, the solubility of MgO is only 0.65 mg/100 mL, meaning that it is essentially insoluble.
High lattice energies lead to hard, insoluble compounds with high melting points.
The Born–Haber Cycle
In principle, lattice energies could be measured by combining gaseous cations and anions to form an ionic solid and then measuring the heat evolved. Unfortunately, measurable quantities of gaseous ions have never been obtained under conditions where heat flow can be measured. Instead, lattice energies are found using the experimentally determined enthalpy changes for other chemical processes, Hess’s law, and a thermochemical cycle called the Born–Haber cycle. Developed by Max Born and Fritz Haber in 1919, the Born–Haber cycle describes a process in which an ionic solid is conceptually formed from its component elements in a stepwise manner.
Let’s use the Born–Haber cycle to determine the lattice energy of \(\ce{CsF(s)}\). \(\ce{CsF}\) is a nearly ideal ionic compound because \(\ce{Cs}\) is the least electronegative element that is not radioactive and F is the most electronegative element. To construct a thermochemical cycle for the formation of \(\ce{CsF}\), we need to know its enthalpy of formation, ΔHf, which is defined by the following chemical reaction:
\[2Cs_{(s)}+F_{2(g)} \rightarrow 2CsF_{(s)} \label{21.5.7} \]
Because enthalpy is a state function, the overall \(ΔH\) for a series of reactions is the sum of the values of \(ΔH\) for the individual reactions. We can therefore use a thermochemical cycle to determine the enthalpy change that accompanies the formation of solid CsF from the parent elements (not ions). The Born–Haber cycle for calculating the lattice energy of cesium fluoride is shown in Figure \(\PageIndex{1}\). This particular cycle consists of six reactions, Equation \(\ref{21.5.7}\) plus the following five reactions:
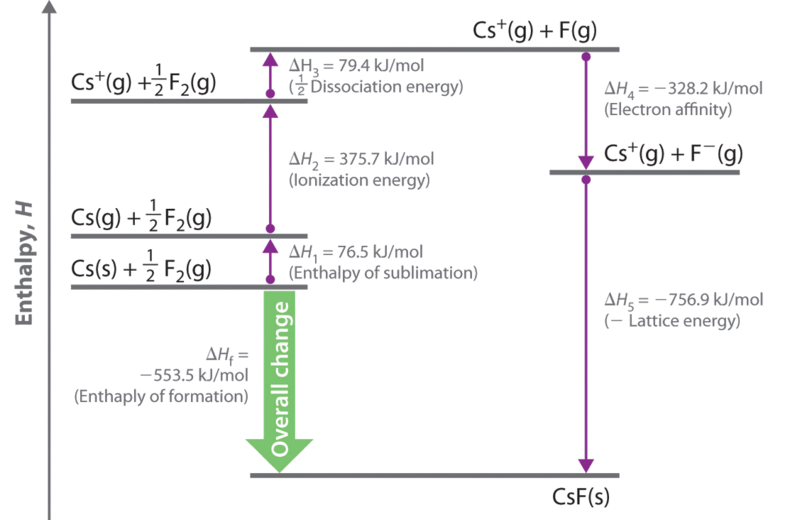
Reaction 1
\[Cs_{(s)} \rightarrow Cs_{(g)}\;\;\; ΔH_1=ΔH_{sub}=76.5\; kJ/mol \label{21.5.8a} \]
This equation describes the sublimation of elemental cesium, the conversion of the solid directly to a gas. The accompanying enthalpy change is called the enthalpy of sublimation (ΔHsub) (Table \(\PageIndex{4}\)) and is always positive because energy is required to sublime a solid.
| Substance | ΔHsub (kJ/mol) |
|---|---|
| Li | 159.3 |
| Na | 107.5 |
| K | 89.0 |
| Rb | 80.9 |
| Cs | 76.5 |
| Be | 324.0 |
| Mg | 147.1 |
| Ca | 177.8 |
| Sr | 164.4 |
| Ba | 180.0 |
|
Source: Data from CRC Handbook of Chemistry and Physics (2004). |
|
Reaction 2:
\[\ce{Cs(g) -> Cs^{+}(g) + e^{-}} \;\;\; ΔH_2=I_1=375.7\; kJ/mol \label{21.5.8b} \]
This equation describes the ionization of cesium, so the enthalpy change is the first ionization energy of cesium. Recall that energy is needed to ionize any neutral atom. Hence, regardless of the compound, the enthalpy change for this portion of the Born–Haber cycle is always positive.
Reaction 3:
\[\ce{1/2 F2(g) -> F(g)} \;\;\; ΔH_3=\frac{1}{2}D=79.4\; kJ/mol \label{21.5.8c} \]
This equation describes the dissociation of fluorine molecules into fluorine atoms, where \(D\) is the energy required for dissociation to occur (Table \(\PageIndex{5}\)). We need to dissociate only \(\ce{1/2}\) mol of \(F_{2(g)}\) molecules to obtain 1 mol of \(F_{(g)}\) atoms. The ΔH for this reaction, too, is always positive because energy is required to dissociate any stable diatomic molecule into the component atoms.
| Substance | D (kJ/mol) |
|---|---|
| H2(g) | 436.0 |
| N2(g) | 945.3 |
| O2(g) | 498.4 |
| F2(g) | 158.8 |
| Cl2(g) | 242.6 |
| Br2(g) | 192.8 |
| I2(g) | 151.1 |
|
Source: Data from CRC Handbook of Chemistry and Physics (2004). |
|
Reaction 4:
\[F_{(g)}+ e^- \rightarrow F^-_{(g)} \;\;\; ΔH_4= EA = –328.2\; kJ/mol \label{21.5.8d} \]
This equation describes the formation of a gaseous fluoride ion from a fluorine atom; the enthalpy change is the electron affinity of fluorine. Recall that electron affinities can be positive, negative, or zero. In this case, ΔH is negative because of the highly negative electron affinity of fluorine.
Reaction 5:
\[ Cs^+_{(g)} + F^–_{(g)}→CsF_{(s)} \;\;\; ΔH_5=–U \label{21.5.8e} \]
This equation describes the formation of the ionic solid from the gaseous ions. Because Reaction 5 is the reverse of the equation used to define lattice energy and U is defined to be a positive number, ΔH5 is always negative, as it should be in a step that forms bonds.
If the enthalpy of formation of CsF from the elements is known (ΔHf = −553.5 kJ/mol at 298 K), then the thermochemical cycle shown in Figure \(\PageIndex{3}\) has only one unknown, the quantity ΔH5 = −U. From Hess’s law, we can write
\[ΔH_f = ΔH_1 + ΔH_2 + ΔH_3 + ΔH_4 + ΔH_5 \label{21.5.9} \]
We can rearrange Equation \(\ref{21.5.9}\) to give
\[−ΔH_5 = ΔH_1 + ΔH_2 + ΔH_3 + ΔH_4 − ΔH_f \label{21.5.10} \]
Substituting for the individual ΔHs, we obtain
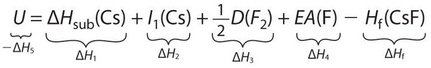
Substituting the appropriate values into this equation gives
\[\begin{align} U &= 76.5\; kJ/mol + 375.7 \;kJ/mol + 79.4\; kJ/mol + (−328.2\; kJ/mole) − (−553.5\; kJ/mol) \nonumber \\[4pt] &= 756.9\; kJ/mol \label{21.5.11} \end{align} \]
U is larger in magnitude than any of the other quantities in Equation \(\ref{21.5.1}\). The process we have used to arrive at this value is summarized in Table \(\PageIndex{6}\).
| Reaction | Enthalpy Change (kJ/mol) | |
|---|---|---|
| (1) | Cs(s) → Cs(g) | ΔHsub = 76.5 |
| (2) | Cs(g) → Cs + (g) + e− | I1 = 375.7 |
| (3) | ½F2(g) → F(g) | ½D = 79.4 |
| (4) | F(g) + e− → F−(g) | EA = −328.2 |
| (5) | Cs + (g) + F−(g) → CsF(s) | −U = −756.9 |
| total | Cs(s) + ½F2(g) → CsF(s) | ΔHf = −553.5 |
Predicting the Stability of Ionic Compounds
Equation \(\ref{21.5.9}\) may be used as a tool for predicting which ionic compounds are likely to form from particular elements. As we have noted, ΔH1 (ΔHsub), ΔH2 (I), and ΔH3 (D) are always positive numbers, and ΔH2 can be quite large. In contrast, ΔH4 (EA) is comparatively small and can be positive, negative, or zero. Thus the first three terms in Equation \(\ref{21.5.9}\) make the formation of an ionic substance energetically unfavorable, and the fourth term contributes little either way. The formation of an ionic compound will be exothermic (ΔHf < 0) if and only if ΔH5 (−U) is a large negative number. This means that lattice energy is the most important factor in determining the stability of an ionic compound. Another example is the formation of \(\ce{BaO}\):
\[\ce{Ba(s) + 1/2 O2(g) -> BaO(s)} \label{21.5.11a} \]
The enthalpy change is just the enthalpy of formation (e.g, \(ΔH=ΔH_f\)) with a Born–Haber cycle is compared with that for the formation of \(\ce{CsF}\) in Figure \(\PageIndex{4}\).

The lattice energy of BaO, with a di-positive cation and a di-negative anion, dominates the Born–Haber cycle.
- Reaction 1: \[Ba_{(s)}→Ba_{(g)} \;\;\; ΔH_1=ΔH_{sub}=180.0\; kJ/mol \label{ 21.5.12} \] More than twice as much energy is required to sublime barium metal (180.0 kJ/mol) as is required to sublime cesium (76.5 kJ/mol).
- Reaction 2: \[Ba_{(s)}→Ba^{2+}_{(g)}+2e^– \;\;\; ΔH_2=I_1+I_2=1468.1\; kJ/mol \label{ 21.5.13} \] Nearly four times the energy is needed to form Ba2+ ions (I1 = 502.9 kJ/mol, I2 = 965.2 kJ/mol, I1 + I2 = 1468.1 kJ/mol) as Cs+ ions (I1 = 375.7 kJ/mol).
- Reaction 3: \[\dfrac{1}{2}O_{2(g)}→O{(g)} \;\;\; ΔH_3=\frac{1}{2}D=249.2\; kJ/mol \label{21.5.14} \] Because the bond energy of O2(g) is 498.4 kJ/mol compared with 158.8 kJ/mol for F2(g), more than three times the energy is needed to form oxygen atoms from O2 molecules as is required to form fluorine atoms from F2.
- Reaction 4: \[O_{(g)} + 2e^– →O^{2–}_{(g)} \;\;\; ΔH_4=EA_1+EA_2=603\; kJ/mol \label{21.5.15} \] Forming gaseous oxide (O2−) ions is energetically unfavorable. Even though adding one electron to an oxygen atom is exothermic (EA1 = −141 kJ/mol), adding a second electron to an O−(g) ion is energetically unfavorable (EA2 = +744 kJ/mol)—so much so that the overall cost of forming O2−(g) from O(g) is energetically prohibitive (EA1 + EA2 = +603 kJ/mol). If the first four terms in the Born–Haber cycle are all substantially more positive for BaO than for CsF, why does BaO even form? The answer is the formation of the ionic solid from the gaseous ions (Reaction 5):
- Reaction 5: \[Ba^{2+}_{(g)}+O^{2–}_{(g)} → BaO_{(s)} \;\;\; ΔH_5=–U \label{21.5.16} \]
Remember from Equations \(\ref{21.5.1}\) and \(\ref{21.5.6}\) that lattice energies are directly proportional to the product of the charges on the ions and inversely proportional to the internuclear distance. Although the internuclear distances are not significantly different for BaO and CsF (275 and 300 pm, respectively), the larger ionic charges in \(\ce{BaO}\) produce a much higher lattice energy. Substituting values for \(\ce{BaO}\) (ΔHf = −548.0 kJ/mol) into the equation and solving for U gives:
\[\begin{align*} U&=ΔH_{sub}(Ba)+[I_1(Ba)+I_2(Ba)]+\frac{1}{2}D(O_2)+[EA_1(O)+EA_2(O)]−ΔH_f(BaO)\;\;\; \label{21.5.17} \\[4pt] &=180.0\; kJ/mol + 1468.1 \; kJ/mol + 249.2\; kJ/mol + 603\; kJ/mol−(−548.0\; kJ/mol) \\[4pt] &= 3048\; kJ/mol \end{align*} \]
If the formation of ionic lattices containing multiple charged ions is so energetically favorable, why does CsF contain Cs+ and F− ions rather than Cs2+ and F2− ions? If we assume that U for a Cs2+F2− salt would be approximately the same as U for BaO, the formation of a lattice containing Cs2+ and F2− ions would release 2291 kJ/mol (3048 kJ/mol − 756.9 kJ/mol) more energy than one containing Cs+ and F− ions. To form the Cs2+ ion from Cs+, however, would require removing a 5p electron from a filled inner shell, which calls for a great deal of energy: I2 = 2234.4 kJ/mol for Cs. Furthermore, forming an F2− ion is expected to be even more energetically unfavorable than forming an O2− ion. Not only is an electron being added to an already negatively charged ion, but because the F− ion has a filled 2p subshell, the added electron would have to occupy an empty high-energy 3s orbital. Cesium fluoride, therefore, is not Cs2+F2− because the energy cost of forming the doubly charged ions would be greater than the additional lattice energy that would be gained.
Lattice energy is usually the most important energy factor in determining the stability of an ionic compound.
Use the thermodynamics data in the reference tables to calculate the lattice energy of \(\ce{MgH2}\).
Given: chemical compound and data from figures and tables
Asked for: lattice energy
Strategy:
A Write a series of stepwise reactions for forming \(\ce{MgH2}\) from its elements via the gaseous ions.
B Use Hess’s law and data from the specified figures above and tables to calculate the lattice energy.
Solution:
A Hess’s law allows us to use a thermochemical cycle (the Born–Haber cycle) to calculate the lattice energy for a given compound. We begin by writing reactions in which we form the component ions from the elements in a stepwise manner and then assemble the ionic solid:
| (1) | \(Mg_{(s)} → Mg_{(g)}\) | \(ΔH_1=\) | \(ΔH=ΔH_{sub}(Mg)\) |
| (2) | \(Mg_{(g)} → Mg^{2+}_{(g)} + 2e^-\) | \(ΔH_2=\) | \(I_1(Mg)+I_2(Mg\) |
| (3) | \( H_{2(g)} → 2H_{(g)}\) | \(ΔH_3=\) | \(D(H_2)\) |
| (4) | \(2H_(g)+2e^− →2H^-_{(g)}\) | \(ΔH_4=\) | \(2EA(H)\) |
| (5) | \(Mg2+(g) +2H^−_{(g)} → MgH_{2(s)}\) | \(ΔH_5=\) | \(−U\) |
| total | \(Mg_{(s)}+H_{2(g)} \rightarrow MgH_{2(s)}\) | \(ΔH=\) | \(ΔH_f\) |
B Table A6 lists the first and second ionization energies for the period 3 elements [I1(Mg) = 737.7 kJ/mol, I2(Mg) = 1450.7 kJ/mol]. First electron affinities for all elements are given in Figure \(\PageIndex{1}\) [EA(H) = −72.8 kJ/mol]. Table \(\PageIndex{4}\) lists selected enthalpies of sublimation [ΔHsub(Mg) = 147.1 kJ/mol]. Table \(\PageIndex{5}\) lists selected bond dissociation energies [D(H2) = 436.0 kJ/mol]. Enthalpies of formation (ΔHf = −75.3 kJ/mol for MgH2) are listed in Table T2. From Hess’s law, ΔHf is equal to the sum of the enthalpy changes for Reactions 1–5:
For MgH2, U = 2701.2 kJ/mol. Once again, lattice energy provides the driving force for forming this compound because ΔH1, ΔH2, ΔH3 > 0. When solving this type of problem, be sure to write the chemical equation for each step and double-check that the enthalpy value used for each step has the correct sign for the reaction in the direction it is written.
Use data from the reference tables to calculate the lattice energy of \(\ce{Li2O}\). Remember that the second electron affinity for oxygen [O−(g) + e− → O2−(g)] is positive (+744 kJ/mol).
- Answer
-
2809 kJ/mol
Summary
Ionic compounds have strong electrostatic attractions between oppositely charged ions in a regular array. The lattice energy (\(U\)) of an ionic substance is defined as the energy required to dissociate the solid into gaseous ions; \(U\) can be calculated from the charges on the ions, the arrangement of the ions in the solid, and the internuclear distance. Because U depends on the product of the ionic charges, substances with di- or tripositive cations and/or di- or trinegative anions tend to have higher lattice energies than their singly charged counterparts. Higher lattice energies typically result in higher melting points and increased hardness because more thermal energy is needed to overcome the forces that hold the ions together. Lattice energies cannot be measured directly but are obtained from a thermochemical cycle called the Born–Haber cycle, in which Hess’s law is used to calculate the lattice energy from the measured enthalpy of formation of the ionic compound, along with other thermochemical data. The Born–Haber cycle can be used to predict which ionic compounds are likely to form. Sublimation, the conversion of a solid directly to a gas, has an accompanying enthalpy change called the enthalpy of sublimation.
Key Takeaway
- The lattice energy is usually the most important energy factor in determining the stability of an ionic compound.


