16.E: Solubility and Precipitation (Exercises)
- Page ID
- 50307
These are homework exercises to accompany the Textmap created for "Principles of Modern Chemistry" by Oxtoby et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here.
Q5
State the balanced equation representing the dissolution of potassium chromate and write its solubility product expression.
- Answer
-
\[ \mathrm{K_2CrO_4 \rightleftharpoons 2K^+ + CrO_4^{2-} }\nonumber \]
\[ \mathrm{K_{sp} = [K^+]^2 [CrO_4^{2-}] }\nonumber \]
Q11
Consider Mercury(I) bromide. Estimate the concentration of \(Hg_2^{2+}\) and \(Br^-\) given the \(K_{sp}\) as 5.6 x 10-23.
- Answer
-
\[\ce{Hg2Br2 (s) <=> Hg2^{2+} (aq) + 2Br^- (aq)}\]
\[K_{sp}=5.6\cdot 10^{-23}=[Hg_{2}^{2+}][Br^{-}]^{2}=x(2x)^{2}\]
\[\mathrm{x = 2.41 \times 10^{-8} = [Hg_2^{2+}] } \nonumber \]
\[\mathrm{[Br^-] = 4.82 \times 10^{-8}}\nonumber \]
Q13
The solubility product constant of Calcium chlorate (\(Ca(ClO_3)_2\)) of water is 7.1 × 10-7 at 25oC. How many grams of \(Ca(ClO_3)_2\) were dissolved in 750 mL?
- Answer
-
First, write out the solubility product constant expression for \(\ce{Ca(ClO3)2}\)
\[\ce{ Ca(ClO3)2 (s) <=> Ca^{2+} (aq) + 2 ClO3^- (aq)} \nonumber \]
\[\mathrm{K_{sp} = [Ca^{2+}][ClO_3^-]^2}\nonumber \]
ICE Table \(Ca(ClO_3)_2\) \(Ca^{2+}\) \(ClO_3^-\) Initial - 0 0 Change - +x +2x Equilibrium - x 2x \(Ca(ClO_3)_2\) does not matter because it is a solid
\[\mathrm{K_{sp}= [x] \cdot [2x]^2}\nonumber \]
\[\mathrm{7.1 \times 10^{-7} = 4x^3}\nonumber \]
\[\mathrm{x = 0.0056 \; M}\nonumber \]
The number of moles of \(Ca^{2-}\) is the same as the number of moles of \(Ca(ClO_3)_2\) because matter cannot be created or destroyed.
\[\mathrm{\dfrac{0.0056 \: moles}{L} \times 0.750 \: L = 0.0042 \; moles \; Ca(ClO_3)_2}\nonumber \]
Finally, the mass can be calculated by multiplying the number of moles with the molar mass:
\[\mathrm{0.0042 \: moles Ca(ClO_3)_2 \times (\dfrac{206.98 \: g}{1 \; mole} ) = 0.872 \: g }\nonumber \]
Q15
At 25°C, water dissolves 0.8108g of PbCl2 per liter, calculate the Ksp of PbCl2 at 25°C.
- Answer
-
\[PbCl_{2}(s)\rightleftharpoons Pb^{2+}(aq)+2Cl^{-}(aq)\nonumber \]
\[K_{sp}=[Pb^{2+}]\cdot [Cl^{-}]^{2}\nonumber \]
\[n(PbCl_{2})=\dfrac{0.8108g}{278.1g/mol}=2.9155 \times 10^{-3}mol=n(Pb^{2+})=0.5n(Cl^{-})\nonumber \]
\[K_{sp}=\dfrac{2.9155 \times 10^{-3}mol}{1L}\cdot (\dfrac{5.831 \times 10^{-3}mol}{1L})^{2}=9.91 \times 10^{-8}\nonumber \]
Q17
0.986635g of \(\ce{BaCO_3}\) is dissolved in 1.00dm3 water at 80oC. the solution was then cooled down to 25oC. Given that the Ksp of \(\ce{BaCO_3}\) in water is 2.58x10-9 at 25oC, determine with an explanation whether or not a precipitate will form at 25oC.
- Answer
-
x moles of BaCO3 dissolves into x moles of Ba2+ and x moles CO32- due to equal stoichiometric coefficients (since solution is 1.00L, the moles also equal to molarities). Calculate the moles of BaCO3, then square the result to find Qsp, then compare Qsp to Ksp at 250C.
\[\mathrm{moles \: of \; BaCO_3 = 0.986635 \; g \times (137.327 \dfrac{g}{mol} + 12 \dfrac{g}{mol} + 3 \times 16 \dfrac{g}{mol}) = 5.0 \times 10^{-3} \; mol }\nonumber \]
\[\mathrm{Q_{sp} = (5.0 \times 10^{-3} \; M)^2 = 2.5 \times 10^{-5} }\nonumber \]
\[\mathrm{2.5 \times 10^{-5} > 2.58 \times 10^{-9}}\nonumber \]
\[\mathrm{Q_{sp} > K_{sp} }\nonumber \]
Therefore, precipitate forms.
Q19
Suppose that you take a solution of 500.0-mL of 0.001234 M \(FeF_2\) and mix it well with a 500.0-mL solution of 0.003142 M \(KOH\) at 25ºC. Given that \(\mathrm{K_{sp} = 4.87 \times 10^{-17} }\) is for \(Fe(OH)_2\), determine whether or not a precipitate will be formed from the mixture.
- Answer
-
Before starting any calculations it is important to write down the equation for precipitation of the Fe(OH)2.
\[\ce{Fe(OH)2}(s) \rightleftharpoons \ce{Fe^2+}(aq)+\ce{2OH-}(aq)\nonumber \]
State the solubility product expression and set it equal to the solubility product constant:
\[ K_{\ce sp}={[Fe^2+][OH-]^2}=4.87\times10^{-17}\nonumber \]
Now that the essential basic steps are out of the way, find the new concentrations of both \(\ce{Fe^{2+} }\) Fe2+ and OH- by first finding the number of moles in the original unmixed solutions and then dividing that number by the total new volume in liters.
\[\textrm{moles Fe}^{2+}=\textrm{500} \cancel{mL}\;\left(\dfrac{\textrm{1} \cancel{L}\;}{\textrm{1000} \cancel{mL}\;}\right)\left(\dfrac{0.001234\textrm{ mol}}{\textrm{1} \cancel{L}\;}\right )=6.17\times10^{-4}\textrm{ mol Fe}^{2+}\nonumber \]
\[\textrm[{Fe}^{2+}]=\left(\dfrac{6.17\times10^{-4}\textrm{ mol Fe}^{2+}}{\textrm{1000} \cancel{mL}\;}\right)\left(\dfrac{\textrm{1000} \cancel{ mL}\;}{\textrm{1 L}} \right )=6.17\times10^{-4}\textrm{ M Fe}^{2+}\nonumber \]
\[\textrm{moles OH-}=\textrm{500} \cancel{mL}\;\left(\dfrac{\textrm{1} \cancel{L}\;}{\textrm{1000} \cancel{mL}\;}\right)\left(\dfrac{0.003142\textrm{ mol}}{\textrm{1} \cancel{L}\;}\right )=1.57\times10^{-3}\textrm{ mol OH-}\nonumber \]
\[\textrm[{OH-}]=\left(\dfrac{1.57\times10^{-3}\textrm{ mol OH-}}{\textrm{1000} \cancel{mL}\;}\right)\left(\dfrac{\textrm{1000} \cancel{ mL}\;}{\textrm{1 L}} \right )=1.57\times10^{-3}\textrm{ M OH-}\nonumber \]
Now that the new concentrations have been found they can be substituted in the Qsp equation and solved for.
\[ Q_{\ce sp}={[6.17\times10^{-4}][1.57\times10^{-3}]^2}=1.52\times10^{-9}\nonumber \]
As shown above the \(\mathrm{Q_{sp} > K_{sp}}\), therefore a precipitate does in fact form.
Q23
The solubility product constant of \(\ce{Ag_2CO_3}\) is \(\mathrm{8.1 \times 10^{-12}}\) at 25oC. Calculate \(\ce{[Ag^+]}\) and \(\ce{[CO_3^{2-}]}\) in the solution at equilibrium when 6 mL of 0.1M \(\ce{Na_2CO_3}\) are mixed with 3 mL of 0.5M \(\ce{AgNO_3}\).
- Answer
-
\[2AgNO_{3(aq)}+Na_2CO_{3(aq)} \rightleftharpoons Ag_{2}CO_{3(s)}+2NaNO_{3(aq)}\]
\[mole_{AgNO_{3}}=mole_{Ag^{+}}=(0.003 \; L)(0.5 \; M)=1.5\times 10^{-3}\ mol\]
\[mole_{Na_2CO_{3}}=mole_{CO_{3}^{2-}}=(0.006 \; L)(0.1 \; M)=6\times 10^{-4}\ mol\]
\[Total\ Volume = 3 \; mL + 6 \; mL = 9 \; mL = 0.009 \; L\]
\[M_{CO_{3}^{2-}}=\dfrac{6\times 10^{-4}mol}{0.009 \; L}=0.0667 \; M\]
\[M_{Ag^{+}}=\dfrac{1.5\times 10^{-3}\ mol}{0.009 \; L}=0.1667 \; M\]
\[2Ag^{+} +CO_{3}^{2-} \rightarrow Ag_{2}CO_{3(s)}\]
\(\ce{2Ag^+}\) \(\ce{CO_3^{2-}}\) \(\ce{Ag_2CO_3}\) Initial 0.1667M 0.0667M X Change -2x -x X Equilibrium 0.1667-2x 0.0667-x X \[K_{sp}=8.1\times 10^{-12}=[CO_{3}^{-}][Ag^{+}]^{2}\]
\[8.1\times 10^{-12}=[0.0667-x ][0.1667-2x]^{2}\]
\[x=0.06669999M\]
\[[Ag^{+}]=0.1667-2x=0.03336M\]
\[[CO_{3}^{2-}]=0.0667-x=7.30\times 10^{-9}\]
Q25
Your nemesis has prepared a perfectly saturated solution of CaF2. To sabotage their work, you add 10 M NaF to their solution. How many grams of CaF2 fall out of solution if they had prepared 500 mL.
\(\mathrm{CaF_2 :K_{sp} = 4.0 \times 10^{-11}} \)
- Answer
-
First, calculate the molar solubility of CaF2 from it's Ksp with the expression:
\[K_{sp} = (s)(2s)^2= 4s^{3}\nonumber \]
\[4.0 \times 10^{-11} = 4s^3\nonumber \]
\[s = 2.15 \times 10^{-4}\nonumber \]
Then, create an ICE table for the addition of F- as NaF:
Products \(\ce{F^-}\) \(\ce{Ca^{2+}}\) Initial s+10 s Change -2x -x Equilibrium (s+10) -2x s-x Now, it's reasonable to assume that 10>>x and s, so our expression simplifies to:
\(K_{sp} = 10^{2}(s-x)\)
Solving for x yields the moles/L which fall out, so multiplying x by 0.5 L (500 mL) yields the correct answer.
\[K_{sp} = 4.0 \times 10^{-11} = 10^2(s-x)\nonumber \]
\[x = 0.000215 \; M\nonumber \]
\[0.5 \; L (0.000215 \; M) (78.07 \; \dfrac{g}{mol}) = 0.00839 \; g\nonumber \]
Q27
Given copper(II) hydroxide, \(\ce{Cu(OH)_2}\). The concentration of \(\ce{Cu^{2+}}\) and \(\ce{OH^{-}}\) at equilibrium in 25°C water is 1.765 x 10-7M and 3.530 x 10-7M respectively.
- Find the Ksp.
- Find the molar solubility of \(\ce{Cu(OH)_2}\) in 0.100M \(\ce{NaOH}\).
- Answer
-
\[Cu(OH)_{2(s)}\rightleftharpoons Cu_{(aq)}^{2+}+2OH_{(aq)}^{-}\]
1)
Since the solubilities given are already at equilibrium, Ksp is found as such:
\[K_{sp}= [Cu^{2+}][OH^{-}]^{2}=(1.765 \times 10^{-7}M)(3.530 \times 10^{-7}M)^{2}=2.2 \times 10^{-20}\]
2)
ICE Table \(\mathrm{Cu(OH)_{2(s)}}\) \(\mathrm{Cu^{2+}_{(aq)}}\) \(\mathrm{OH^-_{(aq)}}\) Initial - 0 0.100 Change - +Z +2Z Equilibrium - Z 0.100+2Z Apply the ice table result to the Ksp found in 1), we get
\[K_{sp}=2.2\times 10^{-20} =[Cu^{2+}][OH^{-}]^{2}=(z)(0.100+2z)^{2}\]
Z can be found either by plugging in quadratic formula or finding intersection in a graphing calculator.
\[K_{sp}=2.2\times 10^{-20} =(z)(0.100+2z)^{2}\]
\[\mathrm{z = 2.2 \times 10^{-18} \; M}\nonumber \]
Q28
Barium Carbonate (BaCO3) has a solubility product of Ksp = 8.1 x 10-9 at 25°C for the equilibrium
\[BaCO_3 \rightleftharpoons Ba^{2+} + CO_3^{2-} \nonumber \]
- Calculate the molar solubility of Barium Carbonate in the water at 25°C.
- Calculate the molar solubility of Barium Carbonate in 0.1M PbCO3.
- Answer
-
a) The expression for solubility product is
$$[Ba^{2+}][{CO_{3}}^{2-}] = K_{sp}$$
Let \[[Ba^{2+}] = S\]
\[S^{2} = K_p = 8.1 \times 10^{-9}\]
Hence, S = 9 x 10-5
Molar Solubility of Barium Carbonate = 9 x 10-5 M
b) due to the common ion effect, \(PbCO_3\) reduces the molar solubility of Barium Carbonate.
\[BaCO_{3} \rightleftharpoons Ba^{2+}\:\:\:\:+\:\:\:\: CO^{2-}_3\]
\(\ce{Ba^{2+}}\) \(\ce{CO^{2-}_3}\) Initial 0 0.1 Change +S +S Final +S 0.1+S \[[Ba^{2+}][{CO_3}^{2-}] = K_{sp}\]
\[S(0.1+S) = K_{sp}\]
\[S+0.1 \approx 0.1\]
⇒ \[S(0.1) = K_{sp}\]
⇒ \[S = \dfrac{8.1\times10^{-9}}{0.1} = 8.1\times10^{-8}\]
⇒ \[S = 8.1 \times 10^{-8} << 0.1\]
Hence, Molar Solubility = 8.1 x 10-8 M
Q33
Determine how will the solubility of the following compounds change (increase, decrease, or unchanged) if the neutral solution is made to be more acidic. Explain your answer in one sentence.
- \(\ce{NO_3^-}\)
- \(\ce{NH_3}\)
- \(\ce{CO_3^{2-}}\)
- Answer
-
As the acidity of a solution increases, the solubility of salts consist of conjugate bases of weak acids will increases.
- \(\ce{NO_3^-}\) is the conjugate base of a strong acid so the solubility will not change
- \(\ce{NH_3}\) is the conjugate base of a weak acid so the solubility will increase
- \(\ce{CO_3^{2-}}\) is also a conjugate base of a weak acid so the solubility will increase
Q37
18-crown-6, or \(\ce{C_12H_24O_6}\), is an organic compound that can bind to group 1 metal ions by wrapping around them when in aqueous solutions. Due to its particular size, it can fit the \(K^+\) ion better than any other.
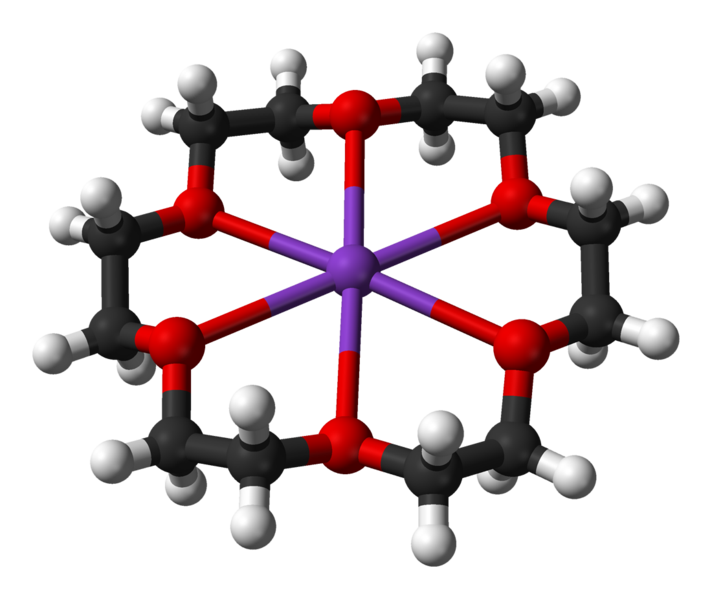
Ball-and-stick model of the 18-crown-6 potassium complex in crystalline (18-crown-6)potassium chlorochromate, [K(C12H24O6)][CrClO3]. X-ray diffraction data from S. A. Kotlyar, R. I. Zubatyuk, O. V. Shishkin, G. N. Chuprin, A. V. Kiriyak and G. L. Kamalov (February 2005). "(18-Crown-6)potassium chlorochromate". Acta. Cryst. E61 (2): m293-m295. DOI:10.1107/S1600536805000085. (Public domain; Ben Mills).
This physical property can be seen in the equilibrium constants for 18-crown-6 and various alkali metals:
\(\ce{Na+_{(aq)} + C_12H_24_O_{6(aq)} \rightarrow Na-crown+_{(aq)}}\)
K = 6.6
\(\ce{K+_{(aq)} + C_12H_24_O_{6(aq)} \rightarrow K-crown+_{(aq)}}\)
K = 111.6
\(\ce{Rb+_{(aq)} + C_12H_24_O_{6(aq)} \rightarrow Rb-crown+_{(aq)}}\)
K = 36
If an aqueous solution is made that is 0.006 M in both 18-crown-6 and Rb+, what is the concentration of unbound Rb+ at equilibrium? If the same solution is made, but with K+ instead of Rb+ ions, what is the concentration of unbound K+ ions at equilibrium?
- Answer
-
First, construct an ICE table.
\[\ce{Rb+_{aq} + C_12H_24O_{6(aq)} \rightleftharpoons Rb-crown+_{aq}}\nonumber \]
\(\ce{Rb^+}\) \(\ce{C_{12}H_{24}O_6}\) Rb-crown+ I 0.006 0.006 0 C -x -x +x E 0.006-x 0.006-x x Then, use the K value of the reaction to solve for x. Use x to solve for the concentration of the desired ion.
\( K = \dfrac{[Rb-crown+]}{[Rb+][C_{12}H_{24}O_6]} \)
\( 36 = \dfrac{[x]}{[0.006-x][0.006-x]} \)
\( x = 9.2954 \times 10^{-4} \)
\( [Rb^+] = 0.0507 M\)
Repeat this process for the other reaction.
\(\ce{K+_{aq} + C_{12}H_{24}O_{6(aq)} \rightleftharpoons K-crown^+_{aq}}\)
\(\ce{K^+}\) \(\ce{C_{12}H_{24}O_6}\) K-crown+ I 0.006 0.006 0 C -x -x +x E 0.006-x 0.006-x x \( K = \dfrac{[K-crown^+]}{[K^+][C_{12}H_{24}O_6]} \)
\( 111.6 = \dfrac{[x]}{[0.006-x][0.006-x]} \)
\( x = 0.0019 \)
\( [K^+] = 0.0041 M\)
Q39
Is it easier to dissolve CuBr into 1M of NaBr solution than to dissolve it into pure water? Does the answer change if when the concentration of NaBr is 0.5M?
- Answer
-
1. When CuBr is added into NaBr solution, the common ion effect occurs. Common ion effect explains that the solvent is responsible for the decrease in the solubility of the precipitate when the soluble compound contains one of the ions of the precipitate that is added to the solution in equilibrium. According to Le Chatelier's principle, some of the ions in excess should be removed from the solution. So it is harder to dissolve CuBr into NaBr solution than dissolve it into pure water.
2. If the concentration is changed to 0.5M, it is still harder to dissolve CuBr in NaBr solution, but less difficult.
Q41
Identify the salt \(\ce{NH_{4}F}\) as either acidic, basic, or neutral. Then explain the mechanism behind why the salt is acidic, basic, or neutral using chemical equations and their \(\ce{K_{a}}\) or \(\ce{K_{b}}\) values provided here and here.
- Answer
-
- For a salt to have an acidic character, it must be able to accept \( \text{OH}^{-} \) ions when it dissociates in an aqueous solution and leave an excess of \( \text{H}^{+} \) in the solution to have an acidic effect.
- For a salt to have a basic character, it must be able to either accept an \( \text{H}^{+} \) when it dissociates in an aqueous solution and leave an excess of \( \text{OH}^{-} \) in the solution to have an basic effect.
\( \ce{ NH_{4}F} \) can be classified as either acidic or basic depending upon which species is present in a greater concentration ( \( \text{H}^{+} \) or \( \text{OH}^{-} \) ) in the solution when \( \ce{NH_{4}F} \) is added.
\( \ce{ NH^{+}_{4(aq)} + F^{-}_{(aq)} + H_2O_{(l)} \rightleftharpoons NH_{3(aq)} + HF_{(aq)} + H_{3}O^{+}_{(aq)} + OH^{-}_{(aq)}} \)
\( \ce{ K_a = 5.6 \times 10^{-10}} \) for \( \ce{NH^{+}_{4(aq)} + H_{2}O_{(1)} \rightleftharpoons NH_{3(aq)} + H_{3}O^{+}_{(aq)}} \)
\( \ce{ K_b = 1.6 \times 10^{-11}} \) for \( \ce{ F^{-}_{(aq)} + H_{2}O_{(1)} \rightleftharpoons HF_{(aq)} + OH^{-}_{(aq)}} \)
Since \( \ce{ {K}_{a} \gt {K}_{b} } \) , \( \ce{ NH_{4}^{+}} \) has a greater affect on the solution and therefore the salt is acidic.
** See key for problem 15.23 on how to calculate \( \ce{K_{b}} \) or \( \ce{K_{a}} \) given \( \ce{K_{a}} \) or \( \ce{K_{b}} \)
Q43
For the complex ion, \(Fe(H_2O)_{6(aq)}^{3+} \), the acid ionization constant for 298K is \(\mathrm{7.7 \times 10^{-3}}\). What is the pH of a 50 mL solution that contains 0.02 mols of \(Fe(NO_3)_2\)?
- Answer
-
Complex ion problems are solved identically to other equilibrium problems.
First, write the balanced equation:
\[ [Fe(H_2O)_{6}]^{3+}_{(aq)} + H_2O_{(aq)} \rightleftharpoons [Fe(H_2O)_5OH]^{2+}_{(aq)} + H_3O^{+}_{(aq)} \nonumber \]
Then, create and solve an ICE table.
\([Fe(H_2O)_6]^{3+}\) \(H_2O\) \(H_3O^{3+} \) \( [Fe(H_2O)_5OH]^{2+}\) 0.40 - 0 0 -x - +x +x 0.40-x - x x From the ICE table:
\[K_a = \dfrac{[H_3O^{3+}][Fe(H_2O)_5OH^{2+}]}{[Fe(H_2O)_6^{3+}]}\nonumber \]
\[7.7 \times 10^{-3} = K_{a} = \dfrac{\left[x\right]\left[x\right]}{\left[0.4-x\right]}\nonumber \]
By rearranging the equation:
\[\mathrm{x^{2}+0.0077x-0.00308=0}\nonumber \]
and using the quadratic,
\[\mathrm{\dfrac{-0.0077\pm{\sqrt {0.0077^{2}-4\left(1\right)\left(-0.00308\right)}}}{2}}\nonumber \]
\[\mathrm{x=0.05178}\nonumber \]
\[\mathrm{pH = -log[H_3O^+] = 1.286}\nonumber \]
Q45
Calculate the concentration of \(\mathrm{H_3O^+}\) in a 0.3 M solution of oxalic acid ( \(\mathrm{pK_{a1} = 1.25 ; pK_{a2} = 3.81}\)).
- Answer
-
\(\mathrm{K_a = 10^{-1.25} =0.0562}\)
Balanced equation: \[\mathrm{C_2H_2O_4 + H_2O \rightleftharpoons C_2HO_4^- + H_3O^+}\nonumber \]
\(\ce{C_2H_2O_4}\) \(\ce{C_2HO_4^{-}}\) \(\ce{H_3O^+}\) I 0.3 0 0 C -x +x +x E 0.3-x x x At equilibrium:
\[\mathrm{\frac{(x)^2}{(0.3-x)} = K_{a1}}\nonumber \]
\[\mathrm{x = 0.1048}\nonumber \]
Balanced equation: \[\mathrm{C_2HO_4^- + H_2O \rightleftharpoons C_2O_4^{2-} + H_3O^+}\nonumber \]
\(\ce{C_2HO_4^-}\) \(\ce{C_2O_4^{2-}}\) \(\ce{H_3O^+}\) I 0.1048 0 0.1048 C -x +x +x E 0.1048-x x x+0.1048 At equilibrium:
\[\mathrm{K_{a2} = 10^{-3.81} }\nonumber \]
\[\mathrm{\frac{x(x+0.1048)}{(0.1048-x)} = K_{a2}}\nonumber \]
\[\mathrm{x = 0.000154}\nonumber \]
\[\mathrm{[H_3O^+] = 0.1048 + 0.000154 \; M = 0.105 \; M}\nonumber \]
Q49
An aqueous solution at 25 °C is 0.10 M in both Ba2+ and Ca2+ ions. One wants to separate the two ions by taking advantage of the different solubility of BaCO3 and CaCO3.
\(BaCO_3 \; K_{sp} = 2.58 \times 10^{-9} \; M \)
\(CaCO_3 \; K_{sp} = 3.36 \times 10^{-9} \; M \)
What is the highest possible CO32- concentration that allows only one salt to present at equilibrium? Which ion is present in the solid, Ba2+ or Ca2+?
- Answer
-
\[\mathrm{BaCO_{3(s)} \leftrightharpoons Ba^{2+}_{(aq)} + CO_{3(aq)}^{2-}}\nonumber \]
\[\mathrm{[CO_3^{2-}] < \dfrac{K_{sp}}{[Ba^{2+}]} = \dfrac{2.58 \times 10^{-9}}{0.1 \; M} = 2.58 \times 10^{-8} \; M \; (Using \: the \; formula \; for \; K_{sp})}\nonumber \]
\[\mathrm{CaCO_{3(s)} \rightleftharpoons Ca_{(aq)}^{2+} + CO_{3(aq)}^{2-} }\nonumber \]
\[\mathrm{[CO_3^{2-}] < \dfrac{K_{sp}}{[Ca^{2+}]} = \dfrac{3.36 \times 10^{-9}}{0.1 \; M} = 3.36 \times 10^{-8} \; M}\nonumber \]
Therefore, the highest possible \(CO_3^{2-}\) concentration that allows only one salt to present at equilibrium is \(\mathrm{2.58 \times 10^{-8} \; M}\). \(Ba^{2+}\) is present in the solid.
Q51
A solution was created by dissolving 1.31 kg of Ba(NO3)2 into 1 L of 0.50 M Ca(NO3)2. Determine which molecule is more soluble. Then determine the concentration of SO4 ion is needed to precipitate all of one molecule but leave the other molecule completely unreacted, use Table E3.
- Answer
-
First we must determine the mass action equation for dissolving the salts:
\[\mathrm{K_{sp} = [Ba^+][SO_4^-] = 1.08 \times 10^{-10} } \nonumber \]
\[\mathrm{K_{sp} = [Ca^+][SO_4^-] = 4.93 \times 10^{-5} } \nonumber \]
We will use CaSO4 as the salt because it is the most soluble.
For Ca+ to to remain in solution, its reaction quotient must remain smaller than then its Ksp:
\[\mathrm{Q = [Ca^+][SO_4^-] < 4.93 \times 10^{-5}}\nonumber \]
Now we just need to impute the concentration of Ca+ and solve for the concentration of SO4 ion:
\[\mathrm{[0.5 \; M][SO_4^-] < 4.93 \times 10^{-5}}\nonumber \]
\[\mathrm{[SO_4^-] < 9.86 \times 10^{-5} \; M}\nonumber \]
So as long as the concentration of SO4 ion is smaller than 9.86 x 10-5 M, no CaSO4 will precipitate
Q55
Let's say you have a solution that is saturated with \(HF\) at a concentration of \([HF] = 0.20 M\).
- If you want some element \(X\) whose concentration is equal to 0.20 M to exist entirely in this solution, what will be the highest pH possible for this mixture? (\(K_a \; of \; HF \; is \; 6.6 \times 10^{-4}\) and \(K \; of \; XF(s) = 2.5 \times 10^{-16})\). Hint: the reaction is given as \(XF(s) + H_2O(l) \leftrightharpoons X(aq) + F^-(aq) + OH^-(aq)\)
- What would be the concentration of some element \(G\) in equilibrium with solid \(GF\) in this solution at the pH value found in part a) given that \(K \; of \; GF(s) = 4.9 \times 10^{-22})\).
- Answer
-
Part a)
Since you have the equation \(XF(s) + H_2O(l) \leftrightharpoons X(aq) + F^-(aq) + OH^-(aq)\), the equilibrium constant K will be equal to
\(K = [X] \; [F^-] \; [OH^-] = 2.5 \times 10^{-16}\)
We now replace these variables above with known derived equations
\(K = [X] \left(\dfrac {[K_a] [HF]}{[H_3O^+]} \right) \left(\dfrac {[K_w]}{[H_3O^+]}\right) = 2.5 \times 10^{-16}\)
Plug in known values and solve for \([H_3O^+]\)
\([H_3O^+] = \sqrt{\dfrac {(0.20) \; (6.6 \times 10^{-4}) \; (0.20) \; (1.0 \times 10^{-14})}{2.5 \times 10^{-16}}}\)
\([H_3O^+] = 0.0325 \; M\)
Now we solve for pH and see that \[pH = -log(0.0325) = 1.50\nonumber \]
Part b)
For part b), we solve the question in a very similar manner as used in part a) with the only differences being a few different variables we plug in. Now, we are solving for our concentration of some element \(G\) using the value of \(H_3O^+\) we found above.
Given the reaction \(GF(s) + H_2O(l) \leftrightharpoons G(aq) + F^-(aq) + OH^-(aq)\), the equilibirum constant K will be equal to
\(K = [G] \; [F^-] \; [OH^-] = 4.90 \times 10^{-22}\)
We now replace these variables above with known derived equations and this time, solve for \([G]\) using the \([H_3O^+]\) value found above
\(K = [G] \; (\dfrac {[K_a] [HF]}{[H_3O^+]}) \; (\dfrac {[K_w]}{[H_3O^+]}) = 4.9 \times 10^{-22}\)
\([G] = 3.92 \times 10^{-7} \; M\)
Q63
200 mL of 0.5M NaCl and 800 mL of 0.10M AgNO3 are mixed together. Calculate the mass of NaNO3 precipitated. Assume:
- that the volumes are additive,
- that AgCl is completely insoluble, and
- any other substances that may form are completely soluble.
- Answer
-
Because NaCl and AgNO3 are strong electrolytes, they dissolve in water by dissociation.
NaNO3 precipitates according to the net ionic equation\[Na^{+}_{(aq)}+NO^{-}_{3(aq)}\rightarrow NaNO_{3(s)}\nonumber \]
First calculate the moles of each ion present.
\[n_{Na^{+}}=0.2L\times 0.5M=0.1 mol Na^{+}\nonumber \]
\[n_{NO_{3}^{-}}=0.8L\times 0.1M= 0.08 mol NO_{3}^{-}\nonumber \]
Assuming that NaNO3 is completely insoluble, the reaction continues until the entire 0.08 mol of NO3- is consumed, which is the limiting reactant, creating 0.08 mol NaNO3.
\[0.08 \; mol \; NaNO_{3}(84.99\dfrac{g}{mol})=6.80 \; g \; NaNO_{3}\nonumber \]
Q69
Siobhan has a \(1L\) solution with containing \(0.050M\) of \(CO_{3\, (aq)}^{2-}\) and \(0.100M\) of \(F_{(aq)}^{-}\). She titrates the solution with a 0.100 M titrand of Iron Iodide, \(FeI_{2}\). The \(K_{sp}\) expressions are:
\(FeCO_{3\, (s)} \rightleftharpoons CO_{3\, (aq)}^{2-} + Fe_{(aq)}^{2+}\) \(K_{sp}\)= \(3.13\times{10}^{-11}\)
\(FeF_{2\, (s)} \rightleftharpoons 2 F_{(aq)}^{-} + Fe_{(aq)}^{2+}\) \(K_{sp}\)= \(2.36\times{10}^{-6}\)
At what volume of iron iodide will the precipitate \(FeCO_{3\, (s)}\) appear? How about \(FeF_{2\, (s)}\)?
- Answer
-
This problem primarily focuses on expanding on how the solubility constant \(K_{sp}\) can predict which solution will titrate first. When Iron Iodide is dripped into the solution, it disassociates into Iron(II) and Iodide Ions.
\(FeI_{2} \rightarrow Fe^{2+}_{(aq)} + 2I^-_{aq}\)
This facilitates a "common ion effect", where the ions from the dissolution of the titrand Iron Iodide contribute to shifting the concentration of the other two reactions:
\(FeCO_{3\, (s)} \rightleftharpoons CO_{3\, (aq)}^{2-} + Fe_{(aq)}^{2+}\)
\(FeF_{2\, (s)} \rightleftharpoons 2 F_{(aq)}^{-} + Fe_{(aq)}^{2+}\)
As seen here, the introduction of \(Fe^{2+}\) ions will mean there is a larger iron ion concentration, which shifts both of the above reactions to the left. This concept that explains this phenomena is colloquially known as Le Chatlier's principle. However, in order to precisely determine at what point precipitate will form, the \(K_{sp}\) values need to be taken into consideration. Recall that the K constant is defined in terms of either concentrations or partial pressures. As the species in this problem are only aqueous solutes and not gaseous compounds, the resulting \(K_{sp}\) will be defined by concentrations as depicted below:
\(FeCO_{3\, (s)} \rightleftharpoons CO_{3\, (aq)}^{2-} + Fe_{(aq)}^{2+}\) \(K_{sp}= \dfrac{\left[CO_{3}^{2-}\right]\left[Fe^{2+}\right]}{1} = 3.13\times{10}^{-11}\)
\(FeF_{2\, (s)} \rightleftharpoons 2 F_{(aq)}^{-} + Fe_{(aq)}^{2+}\) \(K_{sp}= \dfrac{\left[F^{-}\right]^{2}\left[Fe^{2+}\right]}{1} = 2.36\times{10}^{-6}\)
Notice that each \(K_{sp}\) is divided by 1. This is to represent the solid reactants. Also, based on the information above, recognize that, at equilibrium, the product of the concentrations of the two ions should equal to thier \(K_{sp}\), and since the problem provided both \(\left[CO^{2+}_{3}\right]\) and \(\left[F^{-}\right]\). By substituting these concentrations into the respective \(K_{sp}\) formulas, the equations can be algebraically manipulated to provide the \(\left[Fe^{2+}\right]\) at equilibrium. This process is seen below for \(FeF_{2\, s}\). The process is basically the same to finding \(\left[Fe^{2+}\right]\) for \(\left[CO^{2+}_{3}\right]\), but there is no need to square root the value since there is no stoichiometric coefficients for that particular equation. In contrast, \(F^{-}\) has a stoichiometric coefficient of 2). Since only initial concentrations were given, we can determine at which point \(Q_{sp} > K_{sp}\)
\(Q_{sp}= \dfrac{\left[F^{-}\right]^{2}\left[Fe^{2+}\right]}{1} = 2.36\times{10}^{-6}\)
\(Q_{sp}= \left(0.05M\right)^{2}\left[Fe^{2+}\right] = 2.36\times{10}^{-6}\)
\(\left[Fe^{2+}\right] = \dfrac{2.36\times{10}^{-6}}{\left(0.100M^{2}\right)}= 2.36\times10^{-4}M\)
Therefore, \(\left[Fe^{2+}\right]\) for \(FeF_{2}= 2.36\times10^{-4}M\)
And \(\left[Fe^{2+}\right]\) for \(FeCO_{3}=6.26\times10^{-10} M\), using the same method.
What this information tells us is the calculated \(\left[Fe^{2+}\right]\) is the concentration of \(Fe^{2+}\) that one would expect to be in equilibrium at the given concentration of the other ion. Therefore, if \(\left[Fe^{2+}\right]\) is higher than this value, then the resulting reaction quotient will be larger than \(K_{sp}\), causing the reaction to shift towards the product and consequently causing the precipitate to form. From the values, it is clear that \(FeCO_{3\, (s)}\) will end up precipitating first, and then \(FeF_{2\, s}\).
Finding the exact volume that the precipitate for each reaction will form is relatively straightforward. Based on the information overviewed before, after the \(\left[Fe^{2+}\right]\) reaches the calculated point, precipitate will form. Therefore, to find the volume of titrant needed, just set up the following equation:
\( molarity_{titrant}\times{V_{titrant}} = mol_{titrant}= mol_{Fe^{2+} to precipitate}\)
\(0.100M\times{V_{titrant}}= \left(6.26\times10^{-10}M\right)\left(1L\right)\)
\(0.100M\times{V_{titrant}}= 6.26\times10^{-10}mol\)
\(V_{titrant}= \dfrac{6.26\times10^{10}mol}{0.100M}\)
\(V_{titrant}=6.26\times10^{-9}L\) for \(FeCO_{3\, (s)}\) precipitate to form.
Via the same process, \(V_{titrant}=0.00236L\) for \(FeF_{2\, (s)}\) to form.
Abstract: Use \(K_{sp}\) to determine \(Q_{sp}\) concentration \(\left[Fe^{2+}\right]\). Divide by molarity of titrant to get desired volume for precipitate to form.
Q73
Complex ion plays an important role in the level of solubility. For example:
\[Hg^{2+}_{(aq)} + 2I^-_{(aq)} \rightleftharpoons HgI_{2 (s)}\nonumber \]
This reaction results in the formation of solid HgI2. However, when solid HgI2 reacts in the same process:
\[HgI_{2(s)} + I^-_{(aq)} \rightleftharpoons HgI^-_{3(aq)}\nonumber \]
The solubility increases greatly and the reaction results in an aqueous product. Explain this phenomenon.
- Answer
-
The first reaction produces a solid precipitate and the second reaction is soluble because complex ions are created in the reaction. \(HgI_3^-\) is a complex ion, which means it has Hg ion in the center that is surrounded by iodine molecules that are able to act as Lewis bases and attract the protons of the Lewis acid in the reaction. These properties are brought out as a result of the reaction and result in an aqueous product.
Q73
Why does the inclusion of \(NH_3\) increase the solubility of \(CuCl_2\) in an aqueous solution?
- Answer
-
The solubility of Cu2+ increases when NH3 present because NH3 forms a complex ion with Cu2+. The corresponding the chemical reaction for is as follows,
\[\mathrm{CuCl_{2(s)} \rightleftharpoons Cu^{2+}_{(aq)} + 2Cl_{(aq)}^- + 4NH_{3(aq)} \rightleftharpoons [Cu(NH_3)_4]^{2+}}\nonumber \]
The formation of the complex ion pulls equilibrium towards the right which allows more CuCl2 to dissolve.

