14.4: Zero-Order Reactions

A zeroth-order reaction is one whose rate is independent of concentration; its differential rate law is rate = k. We refer to these reactions as zeroth order because we could also write their rate in a form such that the exponent of the reactant in the rate law is 0:

\[\textrm{rate}=-\dfrac{\Delta[\textrm A]}{\Delta t}=k[\textrm{reactant}]^0=k(1)=k \label{14.4.1}\]

Because rate is independent of reactant concentration, a graph of the concentration of any reactant as a function of time is a straight line with a slope of −k. The value of k is negative because the concentration of the reactant decreases with time. Conversely, a graph of the concentration of any product as a function of time is a straight line with a slope of k, a positive value.

The graph of a zeroth-order reaction. The change in concentration of reactant and product with time produces a straight line.

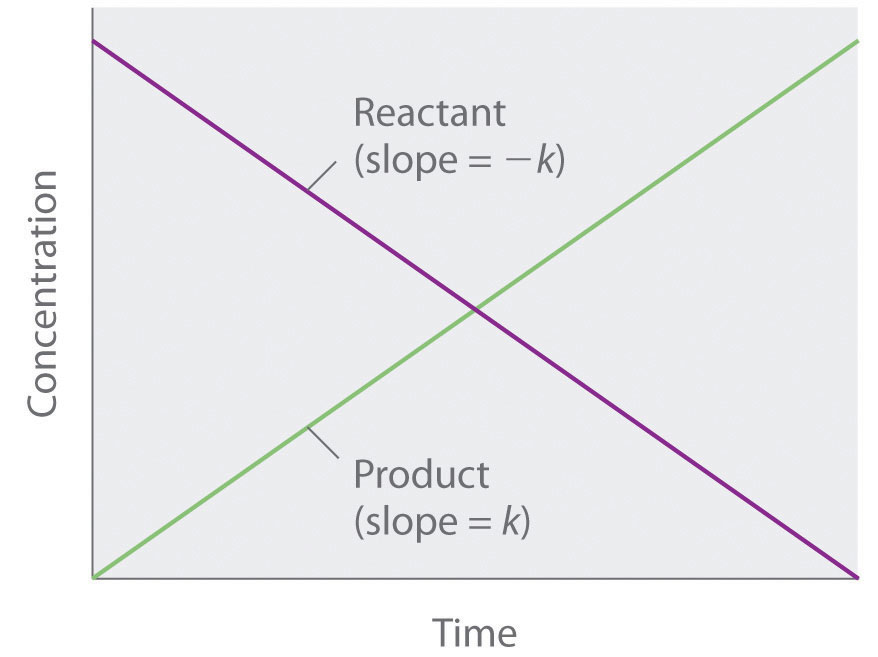
The integrated rate law for a zeroth-order reaction also produces a straight line and has the general form

\[[A] = [A]_0 − kt \label{14.4.2}\]

where [A]₀ is the initial concentration of reactant A. Equation \(\ref{14.4.2}\) has the form of the algebraic equation for a straight line, y = mx + b, with y = [A], mx = −kt, and b = [A]₀.) In a zeroth-order reaction, the rate constant must have the same units as the reaction rate, typically moles per liter per second.

Although it may seem counterintuitive for the reaction rate to be independent of the reactant concentration(s), such reactions are rather common. They occur most often when the reaction rate is determined by available surface area. An example is the decomposition of N₂O on a platinum (Pt) surface to produce N₂ and O₂, which occurs at temperatures ranging from 200°C to 400°C:

\[\mathrm{2N_2O(g)}\xrightarrow{\textrm{Pt}}\mathrm{2N_2(g)}+\mathrm{O_2(g)} \label{14.4.3}\]

Without a platinum surface, the reaction requires temperatures greater than 700°C, but between 200°C and 400°C, the only factor that determines how rapidly N₂O decomposes is the amount of Pt surface available (not the amount of Pt). As long as there is enough N₂O to react with the entire Pt surface, doubling or quadrupling the N₂O concentration will have no effect on the reaction rate. At very low concentrations of N₂O, where there are not enough molecules present to occupy the entire available Pt surface, the reaction rate is dependent on the N₂O concentration. The reaction rate is as follows:

\[\textrm{rate}=-\dfrac{1}{2}\left (\dfrac{\Delta[\mathrm{N_2O}]}{\Delta t} \right )=\dfrac{1}{2}\left (\dfrac{\Delta[\mathrm{N_2}]}{\Delta t} \right )=\dfrac{\Delta[\mathrm{O_2}]}{\Delta t}=k[\mathrm{N_2O}]^0=k \label{14.4.4}\]

Thus the rate at which N₂O is consumed and the rates at which N₂ and O₂ are produced are independent of concentration. As shown in Figure \(\PageIndex{1}\), the change in the concentrations of all species with time is linear. Most important, the exponent (0) corresponding to the N₂O concentration in the experimentally derived rate law is not the same as the reactant’s stoichiometric coefficient in the balanced chemical equation (2). For this reaction, as for all others, the rate law must be determined experimentally.

Figure \(\PageIndex{1}\): A Zeroth-Order Reaction​. This graph shows the concentrations of reactants and products versus time for the zeroth-order catalyzed decomposition of N₂O to N₂ and O₂ on a Pt surface. The change in the concentrations of all species with time is linear.

A zeroth-order reaction that takes place in the human liver is the oxidation of ethanol (from alcoholic beverages) to acetaldehyde, catalyzed by the enzyme alcohol dehydrogenase. At high ethanol concentrations, this reaction is also a zeroth-order reaction. The overall reaction equation is

Figure \(\PageIndex{2}\)

where NAD⁺ (nicotinamide adenine dinucleotide) and NADH (reduced nicotinamide adenine dinucleotide) are the oxidized and reduced forms, respectively, of a species used by all organisms to transport electrons. When an alcoholic beverage is consumed, the ethanol is rapidly absorbed into the blood. Its concentration then decreases at a constant rate until it reaches zero (part (a) in Figure \(\PageIndex{3}\)). An average 70 kg person typically takes about 2.5 h to oxidize the 15 mL of ethanol contained in a single 12 oz can of beer, a 5 oz glass of wine, or a shot of distilled spirits (such as whiskey or brandy). The actual rate, however, varies a great deal from person to person, depending on body size and the amount of alcohol dehydrogenase in the liver. The reaction rate does not increase if a greater quantity of alcohol is consumed over the same period of time because the reaction rate is determined only by the amount of enzyme present in the liver. Contrary to popular belief, the caffeine in coffee is ineffective at catalyzing the oxidation of ethanol. When the ethanol has been completely oxidized and its concentration drops to essentially zero, the rate of oxidation also drops rapidly (part (b) in Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): The Catalyzed Oxidation of Ethanol​ (a) The concentration of ethanol in human blood decreases linearly with time, which is typical of a zeroth-order reaction. (b) The rate at which ethanol is oxidized is constant until the ethanol concentration reaches essentially zero, at which point the reaction rate drops to zero.

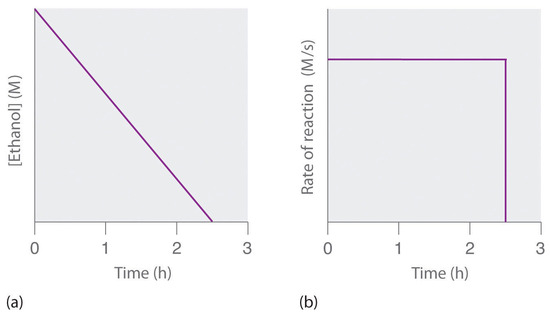
These examples illustrate two important points:

1. In a zeroth-order reaction, the reaction rate does not depend on the reactant concentration.
2. A linear change in concentration with time is a clear indication of a zeroth-order reaction.

Zero-Order Reactions: https://youtu.be/64i7uYsVsSs