4.5: Other Practical Matters in Reaction Stoichiometry

Learning Objectives

• To understand the concept of quantify incomplete reactions, including sequential and parallel reactions.

Theoretical Yields

When reactants are not present in stoichiometric quantities, the limiting reactant determines the maximum amount of product that can be formed from the reactants. The amount of product calculated in this way is the theoretical yield, the amount obtained if the reaction occurred perfectly and the purification method were 100% efficient.

In reality, less product is always obtained than is theoretically possible because of mechanical losses (such as spilling), separation procedures that are not 100% efficient, competing reactions that form undesired products, and reactions that simply do not run to completion, resulting in a mixture of products and reactants; this last possibility is a common occurrence. Therefore, the actual yield, the measured mass of products obtained from a reaction, is almost always less than the theoretical yield (often much less). The percent yield of a reaction is the ratio of the actual yield to the theoretical yield, multiplied by 100 to give a percentage:

\[ percent \, yield = {actual \, yield \, (g) \over theoretical \, yield \, (g) } \times 100 \tag{4.5.1} \]

The method used to calculate the percent yield of a reaction is illustrated in Example \(\PageIndex{1}\).

Example \(\PageIndex{1}\): Novocain

Procaine is a key component of Novocain, an injectable local anesthetic used in dental work and minor surgery. Procaine can be prepared in the presence of H2SO4 (indicated above the arrow) by the reaction

\[ \underset {p-amino benzoic\,acid}{C_7H_7NO_2} + \underset {2-diethylaminoethanol}{C_6H_{15}NO}\,\,\underrightarrow {H_2SO_4} \,\, \underset {procaine}{C_{13}H_{20}N_2O_2} + H_2O\]

If this reaction was carried out using 10.0 g of p-aminobenzoic acid and 10.0 g of 2-diethylaminoethanol, and 15.7 g of procaine were isolated, what is the percent yield?

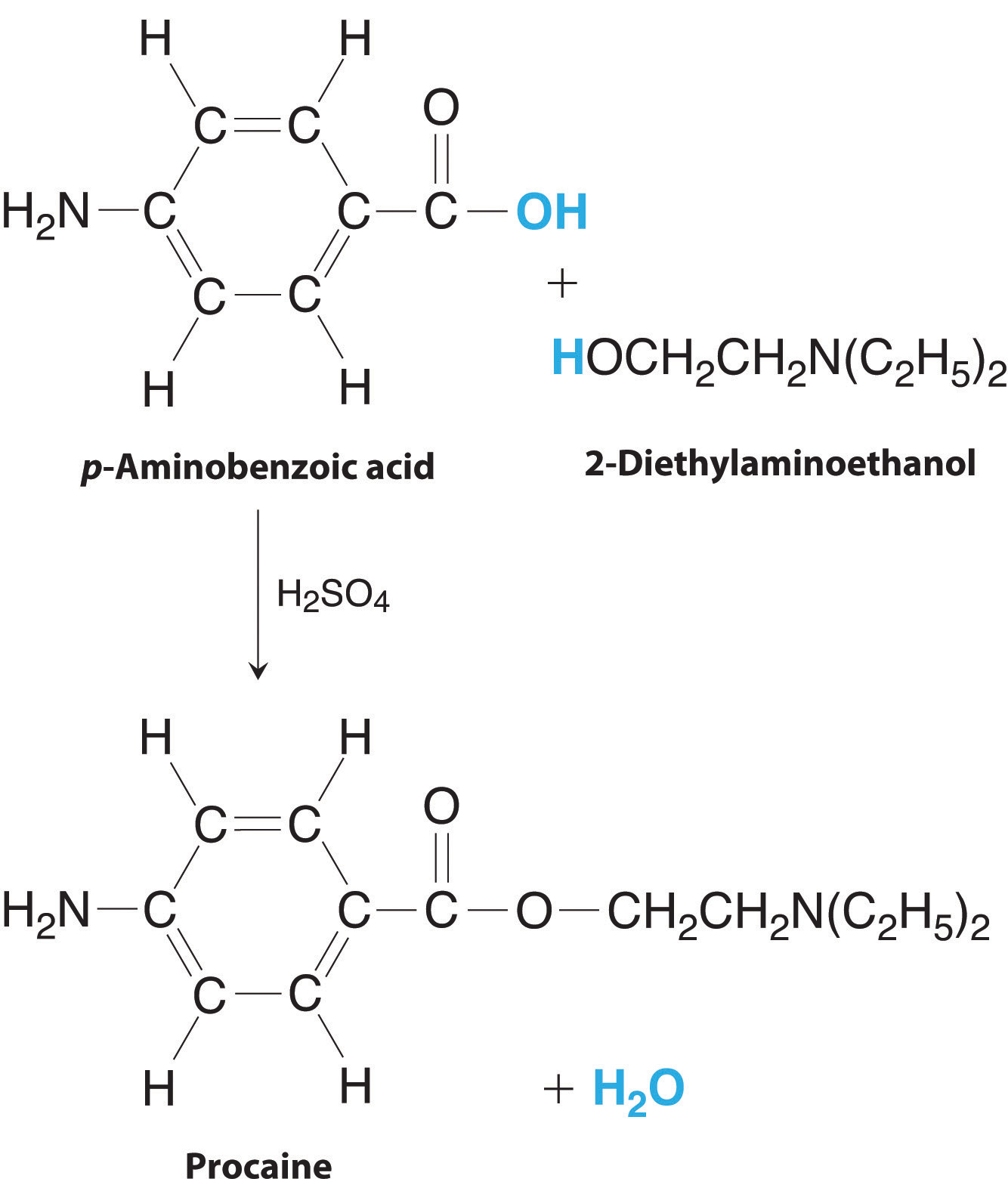
The preparation of procaine. A reaction of p-aminobenzoic acid with 2-diethylaminoethanol yields procaine and water.

Given: masses of reactants and product

Asked for: percent yield

Strategy:

1. Write the balanced chemical equation.
2. Convert from mass of reactants and product to moles using molar masses and then use mole ratios to determine which is the limiting reactant. Based on the number of moles of the limiting reactant, use mole ratios to determine the theoretical yield.
3. Calculate the percent yield by dividing the actual yield by the theoretical yield and multiplying by 100.

Solution:

A From the formulas given for the reactants and the products, we see that the chemical equation is balanced as written. According to the equation, 1 mol of each reactant combines to give 1 mol of product plus 1 mol of water.

B To determine which reactant is limiting, we need to know their molar masses, which are calculated from their structural formulas: p-aminobenzoic acid (C₇H₇NO₂), 137.14 g/mol; 2-diethylaminoethanol (C₆H₁₅NO), 117.19 g/mol. Thus the reaction used the following numbers of moles of reactants:

\[ moles \, p-aminobenzoic \, acid = 10.0 \, g \, \times \, {1 \, mol \over 137.14 \, g } = 0.0729 \, mol \, p-aminbenzoic\, acid \]

\[ moles \, 2-diethylaminoethanol = 10.0 \, g \times {1 \, mol \over 117.19 \, g} = 0.0853 \, mol \, 2-diethylaminoethanol \]

The reaction requires a 1:1 mole ratio of the two reactants, so p-aminobenzoic acid is the limiting reactant. Based on the coefficients in the balanced chemical equation, 1 mol of p-aminobenzoic acid yields 1 mol of procaine. We can therefore obtain only a maximum of 0.0729 mol of procaine. To calculate the corresponding mass of procaine, we use its structural formula (C13H20N2O2) to calculate its molar mass, which is 236.31 g/mol.

\[ theoretical \, yield \, of \, procaine = 0.0729 \, mol \times {236.31 \, g \over 1 \, mol } = 17.2 \, g \]

C The actual yield was only 15.7 g of procaine, so the percent yield is

\[ percent \, yield = {15.7 \, g \over 17.2 \, g } \times 100 = 91.3 \% \]

(If the product were pure and dry, this yield would indicate very good lab technique!)

Exercise \(\PageIndex{1}\): Extraction of Lead

Lead was one of the earliest metals to be isolated in pure form. It occurs as concentrated deposits of a distinctive ore called galena (PbS), which is easily converted to lead oxide (PbO) in 100% yield by roasting in air via the following reaction:

\[ 2PbS_{(s)} + 3O_2 \rightarrow 2PbO_{ (s)} + 2SO_{2 (g)} \]

The resulting PbO is then converted to the pure metal by reaction with charcoal. Because lead has such a low melting point (327°C), it runs out of the ore-charcoal mixture as a liquid that is easily collected. The reaction for the conversion of lead oxide to pure lead is as follows:

\[ PbO_{(s)} + C_{(s)} \rightarrow Pb_{(l)} + CO_{(g)} \]

If 93.3 kg of PbO is heated with excess charcoal and 77.3 kg of pure lead is obtained, what is the percent yield?

Figure used with permission from Wikipedia.

Answer: 89.2%

Percent yield can range from 0% to 100%. In the laboratory, a student will occasionally obtain a yield that appears to be greater than 100%. This usually happens when the product is impure or is wet with a solvent such as water. If this is not the case, then the student must have made an error in weighing either the reactants or the products. The law of conservation of mass applies even to undergraduate chemistry laboratory experiments. A 100% yield means that everything worked perfectly, and the chemist obtained all the product that could have been produced. Anyone who has tried to do something as simple as fill a salt shaker or add oil to a car’s engine without spilling knows the unlikelihood of a 100% yield. At the other extreme, a yield of 0% means that no product was obtained. A percent yield of 80%–90% is usually considered good to excellent; a yield of 50% is only fair. In part because of the problems and costs of waste disposal, industrial production facilities face considerable pressures to optimize the yields of products and make them as close to 100% as possible.

Consecutive Reactions, Simultaneous Reactions, and Overall Reactions

Most of time it takes more than one steps to get desired product. Two more complex reactions are the consecutive and simultaneous reactions. Reactions that are carried out one after another in sequence to yield a final product are called consecutive reactions (e.g., occurring sequenceally):

\[ A \rightarrow Y \rightarrow Z \tag{4.5.2}\]

Any substance that is produced in one step and is consumed in another step of a multistep process is called an intermediate (e.g., \(Y\) in Equation 4.5.2). The Overall Reaction is the chemical equation that expresses all the reactions occurring in a single overall equation.

Example \(\PageIndex{2}\):Purification of \(TiO_2\)

Step 1:

\[2TiO2_{(\text{impure solid})} + 3C_{(s)} +4Cl_{2(g)} \rightarrow 2TiCl_{4(g)} + CO_{2(g)} + 2CO_{(g)}\]

Step 2:

\[2\times [ TiCl_{4(g)} + O_{2(g)} \rightarrow TiO_{2(s)} +2Cl_{2(g)}] \]

Overall:

\[3C_{(s)} + 2O_{2(g)} \rightarrow CO_{2(g)} + 2CO_{(g)}\]

\(TiCl_4\) is an intermediate in this reaction

Example \(\PageIndex{3}\)

How many gram of \(NaBr\) is produced if 55.85g of \(Fe\) is consumed the the following series of reactions?

\[ 3Fe + 3Br_2 \rightarrow 3FeBr_2 \]

\[ 3FeBr_2 + Br_2 \rightarrow Fe_3Br_8\]

\[ Fe_3Br_8 + 4Na_2CO_3 \rightarrow 8NaBr + 4CO_2 + Fe_3O_4\]

Overall reaction:

\[3Fe + 4Br_2 + 4Na_2CO_3 \rightarrow 8NaBr + 4CO_2 + Fe_3O_4\]

Solution

under construction

In simultaneous reactions, two or more substances react independently of one another in separate reactions occurring simultaneously

\[ A \rightarrow Y \tag{4.5.3a}\]

and

\[ B \rightarrow B \tag{4.5.3b}\]

Equations 4.5.3 involve two reactions evolving in parallel, however sometimes there exist a coupling between the two (or more) reactions with shared reactant, intermediates or products. is competition involved, like in the scheme:

\[ A + B \rightarrow Y \tag{4.5.4a}\]

and

\[ A + C \rightarrow Z \tag{4.5.3b}\]

In the above simultaneous reaction, both \(B\) and \(C\) compete with each another for reacting \(A\). This is superficially similar to a common ion effect.

Example \(\PageIndex{4}\): Oxidation of Magnalium

Magnalium is an aluminum alloy with magnesium that exhibits greater strength, greater corrosion resistance, and lower density than pure aluminum. How many grams of \(H_{2(g)}\) are generated if a 0.710 g piece of magnalium (with a 70% Al and 30.0% Mg by mass composition) with excess \(HCl_{(aq)}\)?

Solution

under construction

Summary

• The stoichiometry of a balanced chemical equation identifies the maximum amount of product that can be obtained.

The stoichiometry of a reaction describes the relative amounts of reactants and products in a balanced chemical equation. A stoichiometric quantity of a reactant is the amount necessary to react completely with the other reactant(s). If a quantity of a reactant remains unconsumed after complete reaction has occurred, it is in excess. The reactant that is consumed first and limits the amount of product(s) that can be obtained is the limiting reactant. To identify the limiting reactant, calculate the number of moles of each reactant present and compare this ratio to the mole ratio of the reactants in the balanced chemical equation. The maximum amount of product(s) that can be obtained in a reaction from a given amount of reactant(s) is the theoretical yield of the reaction. The actual yield is the amount of product(s) actually obtained in the reaction; it cannot exceed the theoretical yield. The percent yield of a reaction is the ratio of the actual yield to the theoretical yield, expressed as a percentage.

Contributors and Attributions

Modified by Joshua Halpern (Howard University)