21.5: Energy Changes in Nuclear Reactions
- Page ID
- 21809
- To calculate a mass-energy balance and a nuclear binding energy.
- To understand the differences between nuclear fission and fusion.
Nuclear reactions, like chemical reactions, are accompanied by changes in energy. The energy changes in nuclear reactions, however, are enormous compared with those of even the most energetic chemical reactions. In fact, the energy changes in a typical nuclear reaction are so large that they result in a measurable change of mass. In this section, we describe the relationship between mass and energy in nuclear reactions and show how the seemingly small changes in mass that accompany nuclear reactions result in the release of enormous amounts of energy.
Mass–Energy Balance
The relationship between mass (m) and energy (E) is expressed in the following equation:
\[E = mc^2 \label{Eq1} \]
where
- \(c\) is the speed of light (\(2.998 \times 10^8\; m/s\)), and
- \(E\) and \(m\) are expressed in units of joules and kilograms, respectively.
Albert Einstein first derived this relationship in 1905 as part of his special theory of relativity: the mass of a particle is directly proportional to its energy. Thus according to Equation \(\ref{Eq1}\), every mass has an associated energy, and similarly, any reaction that involves a change in energy must be accompanied by a change in mass. This implies that all exothermic reactions should be accompanied by a decrease in mass, and all endothermic reactions should be accompanied by an increase in mass. Given the law of conservation of mass, how can this be true? The solution to this apparent contradiction is that chemical reactions are indeed accompanied by changes in mass, but these changes are simply too small to be detected. As you may recall, all particles exhibit wavelike behavior, but the wavelength is inversely proportional to the mass of the particle (actually, to its momentum, the product of its mass and velocity). Consequently, wavelike behavior is detectable only for particles with very small masses, such as electrons. For example, the chemical equation for the combustion of graphite to produce carbon dioxide is as follows:
\[\textrm{C(graphite)} + \frac{1}{2}\textrm O_2(\textrm g)\rightarrow \mathrm{CO_2}(\textrm g)\hspace{5mm}\Delta H^\circ=-393.5\textrm{ kJ/mol} \label{Eq2} \]
Combustion reactions are typically carried out at constant pressure, and under these conditions, the heat released or absorbed is equal to ΔH. When a reaction is carried out at constant volume, the heat released or absorbed is equal to ΔE. For most chemical reactions, however, ΔE ≈ ΔH. If we rewrite Einstein’s equation as
\[\Delta{E}=(\Delta m)c^2 \label{Eq3} \]
we can rearrange the equation to obtain the following relationship between the change in mass and the change in energy:
\[\Delta m=\dfrac{\Delta E}{c^2} \label{Eq4} \]
Because 1 J = 1 (kg•m2)/s2, the change in mass is as follows:
\[\Delta m=\dfrac{-393.5\textrm{ kJ/mol}}{(2.998\times10^8\textrm{ m/s})^2}=\dfrac{-3.935\times10^5(\mathrm{kg\cdot m^2})/(\mathrm{s^2\cdot mol})}{(2.998\times10^8\textrm{ m/s})^2}=-4.38\times10^{-12}\textrm{ kg/mol} \label{Eq5} \]
This is a mass change of about 3.6 × 10−10 g/g carbon that is burned, or about 100-millionths of the mass of an electron per atom of carbon. In practice, this mass change is much too small to be measured experimentally and is negligible.
In contrast, for a typical nuclear reaction, such as the radioactive decay of 14C to 14N and an electron (a β particle), there is a much larger change in mass:
\[^{14}\textrm C\rightarrow \,^{14}\textrm N+\,^0_{-1}\beta \label{Eq6} \]
We can use the experimentally measured masses of subatomic particles and common isotopes given in Table 20.1 to calculate the change in mass directly. The reaction involves the conversion of a neutral 14C atom to a positively charged 14N ion (with six, not seven, electrons) and a negatively charged β particle (an electron), so the mass of the products is identical to the mass of a neutral 14N atom. The total change in mass during the reaction is therefore the difference between the mass of a neutral 14N atom (14.003074 amu) and the mass of a 14C atom (14.003242 amu):
\[\begin{align} \Delta m &= {\textrm{mass}_{\textrm{products}}- \textrm{mass}_{\textrm{reactants}}}
\\&=14.003074\textrm{ amu} - 14.003242\textrm{ amu} = - 0.000168\textrm{ amu}\end{align} \label{Eq7} \]
The difference in mass, which has been released as energy, corresponds to almost one-third of an electron. The change in mass for the decay of 1 mol of 14C is −0.000168 g = −1.68 × 10−4 g = −1.68 × 10−7 kg. Although a mass change of this magnitude may seem small, it is about 1000 times larger than the mass change for the combustion of graphite. The energy change is as follows:
\[\begin{align}\Delta E &=(\Delta m)c^2=(-1.68\times10^{-7}\textrm{ kg})(2.998\times10^8\textrm{ m/s})^2 \\ &=-1.51\times10^{10}(\mathrm{kg\cdot m^2})/\textrm s^2=-1.51\times10^{10}\textrm{ J}=-1.51\times10^7\textrm{ kJ}\end{align} \label{Eq8} \]
The energy released in this nuclear reaction is more than 100,000 times greater than that of a typical chemical reaction, even though the decay of 14C is a relatively low-energy nuclear reaction.
Because the energy changes in nuclear reactions are so large, they are often expressed in kiloelectronvolts (1 keV = 103 eV), megaelectronvolts (1 MeV = 106 eV), and even gigaelectronvolts (1 GeV = 109 eV) per atom or particle. The change in energy that accompanies a nuclear reaction can be calculated from the change in mass using the relationship 1 amu = 931 MeV. The energy released by the decay of one atom of 14C is thus
Calculate the changes in mass (in atomic mass units) and energy (in joules per mole and electronvolts per atom) that accompany the radioactive decay of 238U to 234Th and an α particle. The α particle absorbs two electrons from the surrounding matter to form a helium atom.
Given: nuclear decay reaction
Asked for: changes in mass and energy
Strategy:
A Use the mass values in Table 20.1 to calculate the change in mass for the decay reaction in atomic mass units.
B Use Equation \(\ref{Eq4}\) to calculate the change in energy in joules per mole.
C Use the relationship between atomic mass units and megaelectronvolts to calculate the change in energy in electronvolts per atom.
Solution
A Using particle and isotope masses from Table 20.1, we can calculate the change in mass as follows:
\\&=(234.043601\textrm{ amu}+4.002603\textrm{ amu}) - 238.050788\textrm{ amu} = - 0.004584\textrm{ amu}\end{align}\)
B Thus the change in mass for 1 mol of 238U is −0.004584 g or −4.584 × 10−6 kg. The change in energy in joules per mole is as follows:
ΔE = (Δm)c2 = (−4.584 × 10−6 kg)(2.998 × 108 m/s)2 = −4.120 × 1011 J/mol
C The change in energy in electronvolts per atom is as follows:
Calculate the changes in mass (in atomic mass units) and energy (in kilojoules per mole and kiloelectronvolts per atom) that accompany the radioactive decay of tritium (3H) to 3He and a β particle.
- Answer
-
Δm = −2.0 × 10−5 amu; ΔE = −1.9 × 106 kJ/mol = −19 keV/atom
Nuclear Binding Energies
We have seen that energy changes in both chemical and nuclear reactions are accompanied by changes in mass. Einstein’s equation, which allows us to interconvert mass and energy, has another interesting consequence: The mass of an atom is always less than the sum of the masses of its component particles. The only exception to this rule is hydrogen-1 (1H), whose measured mass of 1.007825 amu is identical to the sum of the masses of a proton and an electron. In contrast, the experimentally measured mass of an atom of deuterium (2H) is 2.014102 amu, although its calculated mass is 2.016490 amu:
\[\begin{align}m_{^2\textrm H}&=m_{\textrm{neutron}}+m_{\textrm{proton}}+m_{\textrm{electron}}
\\&=1.008665\textrm{ amu}+1.007276\textrm{ amu}+0.000549\textrm{ amu}=2.016490\textrm{ amu} \end{align}\label{Eq10} \]
The difference between the sum of the masses of the components and the measured atomic mass is called the mass defect of the nucleus. Just as a molecule is more stable than its isolated atoms, a nucleus is more stable (lower in energy) than its isolated components. Consequently, when isolated nucleons assemble into a stable nucleus, energy is released. According to Equation \(\ref{Eq4}\), this release of energy must be accompanied by a decrease in the mass of the nucleus.
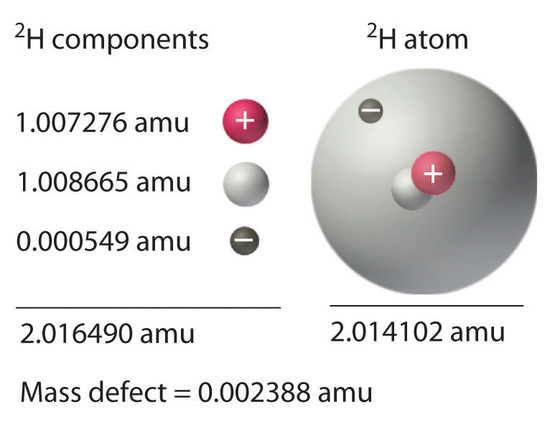
The amount of energy released when a nucleus forms from its component nucleons is the nuclear binding energy (Figure \(\PageIndex{1}\)). In the case of deuterium, the mass defect is 0.002388 amu, which corresponds to a nuclear binding energy of 2.22 MeV for the deuterium nucleus. Because the magnitude of the mass defect is proportional to the nuclear binding energy, both values indicate the stability of the nucleus.
Just as a molecule is more stable (lower in energy) than its isolated atoms, a nucleus is more stable than its isolated components.
Not all nuclei are equally stable. Chemists describe the relative stability of different nuclei by comparing the binding energy per nucleon, which is obtained by dividing the nuclear binding energy by the mass number (A) of the nucleus. As shown in Figure \(\PageIndex{2}\), the binding energy per nucleon increases rapidly with increasing atomic number until about Z = 26, where it levels off to about 8–9 MeV per nucleon and then decreases slowly. The initial increase in binding energy is not a smooth curve but exhibits sharp peaks corresponding to the light nuclei that have equal numbers of protons and neutrons (e.g., 4He, 12C, and 16O). As mentioned earlier, these are particularly stable combinations.
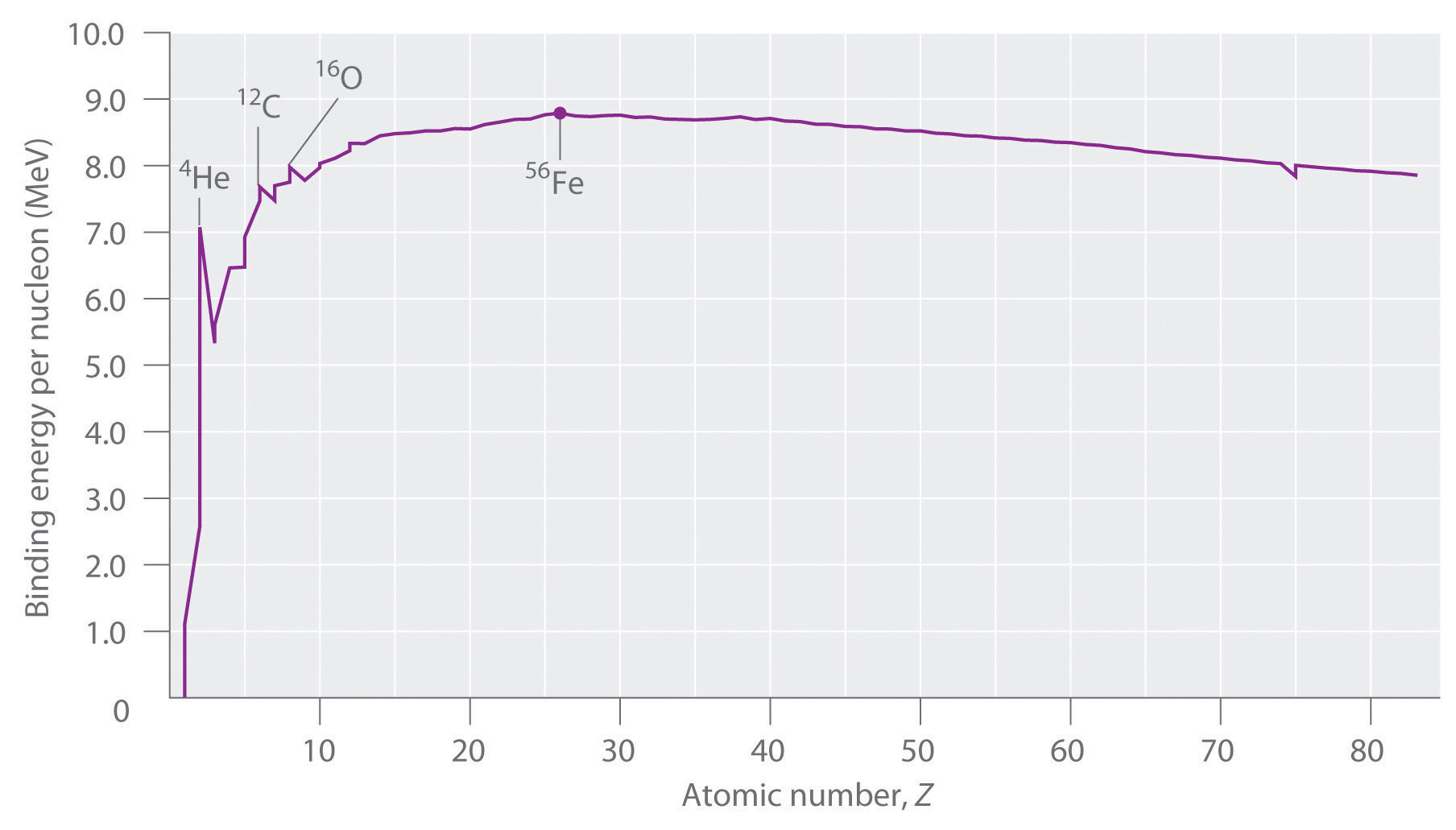
Because the maximum binding energy per nucleon is reached at 56Fe, all other nuclei are thermodynamically unstable with regard to the formation of 56Fe. Consequently, heavier nuclei (toward the right in Figure \(\PageIndex{2}\)) should spontaneously undergo reactions such as alpha decay, which result in a decrease in atomic number. Conversely, lighter elements (on the left in Figure \(\PageIndex{2}\)) should spontaneously undergo reactions that result in an increase in atomic number. This is indeed the observed pattern.
Heavier nuclei spontaneously undergo nuclear reactions that decrease their atomic number. Lighter nuclei spontaneously undergo nuclear reactions that increase their atomic number.
Calculate the total nuclear binding energy (in megaelectronvolts) and the binding energy per nucleon for 56Fe. The experimental mass of the nuclide is given in Table A4.
Given: nuclide and mass
Asked for: nuclear binding energy and binding energy per nucleon
Strategy:
A Sum the masses of the protons, electrons, and neutrons or, alternatively, use the mass of the appropriate number of 1H atoms (because its mass is the same as the mass of one electron and one proton).
B Calculate the mass defect by subtracting the experimental mass from the calculated mass.
C Determine the nuclear binding energy by multiplying the mass defect by the change in energy in electronvolts per atom. Divide this value by the number of nucleons to obtain the binding energy per nucleon.
Solution
A An iron-56 atom has 26 protons, 26 electrons, and 30 neutrons. We could add the masses of these three sets of particles; however, noting that 26 protons and 26 electrons are equivalent to 26 1H atoms, we can calculate the sum of the masses more quickly as follows:
\[\begin{align*}\textrm{calculated mass}&=26(\textrm{mass }^1_1\textrm H)+30(\textrm{mass }^1_0 \textrm n)\\[4pt]
&=26(1.007825)\textrm{amu}+30(1.008665)\textrm{amu}=56.463400\textrm{ amu}\\
\textrm{experimental mass} &=55.934938
\end{align*} \nonumber \]
B We subtract to find the mass defect:
\[\begin{align*}\textrm{mass defect}&=\textrm{calculated mass}-\textrm{experimental mass}
\\&=56.463400\textrm{ amu}-55.934938\textrm{ amu}=0.528462\textrm{ amu}\end{align*} \nonumber \]
C The nuclear binding energy is thus 0.528462 amu × 931 MeV/amu = 492 MeV. The binding energy per nucleon is 492 MeV/56 nucleons = 8.79 MeV/nucleon.
Calculate the total nuclear binding energy (in megaelectronvolts) and the binding energy per nucleon for 238U.
- Answer
-
1800 MeV/238U; 7.57 MeV/nucleon
Summary
Unlike a chemical reaction, a nuclear reaction results in a significant change in mass and an associated change of energy, as described by Einstein’s equation. Nuclear reactions are accompanied by large changes in energy, which result in detectable changes in mass. The change in mass is related to the change in energy according to Einstein’s equation: ΔE = (Δm)c2. Large changes in energy are usually reported in kiloelectronvolts or megaelectronvolts (thousands or millions of electronvolts). With the exception of 1H, the experimentally determined mass of an atom is always less than the sum of the masses of the component particles (protons, neutrons, and electrons) by an amount called the mass defect of the nucleus. The energy corresponding to the mass defect is the nuclear binding energy, the amount of energy released when a nucleus forms from its component particles. In nuclear fission, nuclei split into lighter nuclei with an accompanying release of multiple neutrons and large amounts of energy. The critical mass is the minimum mass required to support a self-sustaining nuclear chain reaction. Nuclear fusion is a process in which two light nuclei combine to produce a heavier nucleus plus a great deal of energy.

