19.3: The Molecular Interpretation of Entropy
- Page ID
- 21907
- To understand entropy from a molecular interpretation
As discussed previously, the second law of thermodynamics argues that all processes must increase the total entropy of the universe. However, the universe if often separated into the System and the Surroundings differing changes of entropy can be observed from a system level perspective. Many processes results in an increase in a system's entropy \(\Delta S > 0\):
- Increasing the volume that a gas can occupy will increase the disorder of a gas
- Dissolving a solute into a solution will increase the entropy of the solute - typically resulting in an increase in the entropy of the system. (Note: the solvation of a solute can sometimes result in a significant decrease in the solvent entropy - leading to a net decrease in entropy of the system)
- Phase changes from solid to liquid, or liquid to gas, lead to an increase in the entropy of the system
Some processes result in a decrease in the entropy of a system \(\Delta S < 0\):
- A gas molecule dissolved in a liquid is much more confined by neighboring molecules than when its in the gaseous state. Thus, the entropy of the gas molecule will decrease when it is dissolved in a liquid
- A phase change from a liquid to a solid (i.e. freezing), or from a gas to a liquid (i.e. condensation) results in an decrease in the disorder of the substance, and a decrease in the entropy
- A chemical reaction between gas molecules that results in a net decrease in the overall number of gas molecules will decrease the disorder of the system, and result in a decrease in the entropy
\[2NO_{(g)} + O_{2(g)} \rightarrow 2NO_{2(g)} \;\;\; \Delta S < 0 \label{19.3.1} \]
What is the molecular basis for the above observations for the change in entropy? Let's first consider the last example, the decrease in entropy associated with a decrease in the number of gas molecules for a chemical reaction
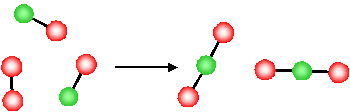
The product of this reaction (\(NO_2\)) involves the formation of a new N-O bond and the O atoms, originally in a separate \(O_2\) molecule, are now connected to the \(NO\) molecule via a new \(N-O\) bond.
- Since they are now physically bonded to the other molecule (forming a new, larger, single molecule) the O atoms have less freedom to move around
- The reaction has resulted in a loss of freedom of the atoms (O atoms)
- There is a reduction in the disorder of the system (i.e. due to the reduction in the degrees of freedom, the system is more ordered after the reaction). \(\Delta S < 0\).
Molecular Degrees of Freedom
The atoms, molecules, or ions that compose a chemical system can undergo several types of molecular motion, including translation, rotation, and vibration (Figure \(\PageIndex{2}\)).
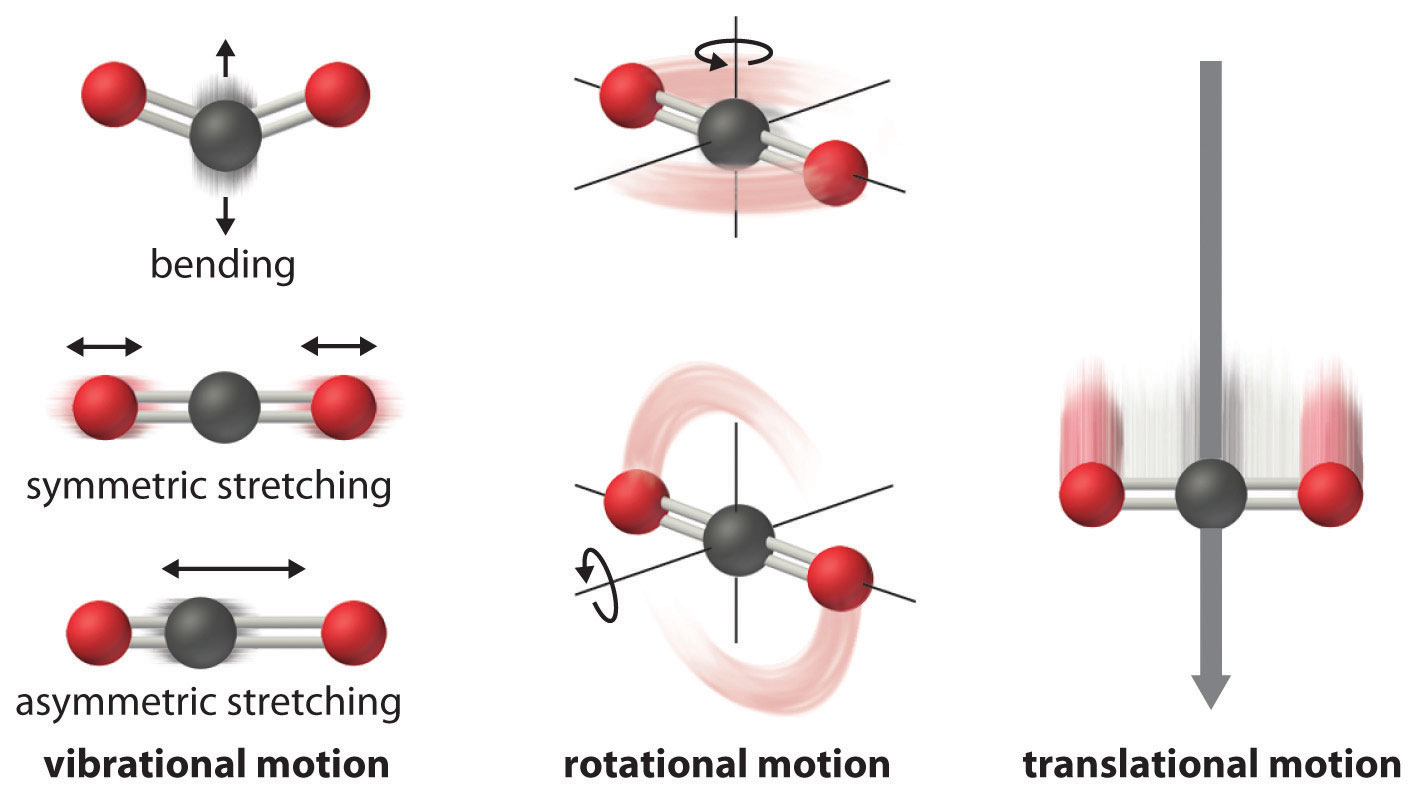
- Translational motion. The entire molecule can move in some direction in three dimensions
- Rotational motion. The entire molecule can rotate around any axis, (even though it may not actually change its position translationally)
- Vibrational motion. The atoms within a molecule have certain freedom of movement relative to each other; this displacement can be periodic motion like the vibration of a tuning fork
These forms of molecular motion are ways in which molecules can store energy. The greater the molecular motion of a system, the greater the number of possible microstates and the higher the entropy.
The Third Law of Thermodynamics
These forms of motion are ways in which the molecule can store energy. The greater the molecular motion of a system, the greater the number of possible microstates and the higher the entropy. A perfectly ordered system with only a single microstate available to it would have an entropy of zero. The only system that meets this criterion is a perfect crystal at a temperature of absolute zero (0 K), in which each component atom, molecule, or ion is fixed in place within a crystal lattice and exhibits no motion (ignoring quantum effects). Such a state of perfect order (or, conversely, zero disorder) corresponds to zero entropy. In practice, absolute zero is an ideal temperature that is unobtainable, and a perfect single crystal is also an ideal that cannot be achieved. Nonetheless, the combination of these two ideals constitutes the basis for the third law of thermodynamics: the entropy of any perfectly ordered, crystalline substance at absolute zero is zero.
The entropy of a pure crystalline substance at absolute zero (i.e. 0 Kelvin) is 0.
Since S = 0 corresponds to perfect order. The position of the atoms or molecules in the crystal would be perfectly defined
- As the temperature increases, the entropy of the atoms in the lattice increase
- Vibrational motions cause the atoms and molecules in the lattice to be less well ordered
The third law of thermodynamics has two important consequences: it defines the sign of the entropy of any substance at temperatures above absolute zero as positive, and it provides a fixed reference point that allows us to measure the absolute entropy of any substance at any temperature.In practice, chemists determine the absolute entropy of a substance by measuring the molar heat capacity (Cp) as a function of temperature and then plotting the quantity Cp/T versus T. The area under the curve between 0 K and any temperature T is the absolute entropy of the substance at T. In contrast, other thermodynamic properties, such as internal energy and enthalpy, can be evaluated in only relative terms, not absolute terms. In this section, we examine two different ways to calculate ΔS for a reaction or a physical change. The first, based on the definition of absolute entropy provided by the third law of thermodynamics, uses tabulated values of absolute entropies of substances. The second, based on the fact that entropy is a state function, uses a thermodynamic cycle similar to those discussed previously.
From classical kinetic theory, all motions cease at absolute zero. However things are more complicated from the more advanced (and more accurate) quantum mechanics. The Heisenberg Uncertainly Principle of quantum mechanics argues that molecules, even at absolute zero, always always have motion. Nonetheless, this motion is often ignored in the introduction of the third law of thermodynamics (which is incorrect of course).
Continued heating of a Solid Lattice
One way of calculating ΔS for a reaction is to use tabulated values of the standard molar entropy (S°), which is the entropy of 1 mol of a substance at a standard temperature of 298 K; the units of S° are J/(mol·K). Unlike enthalpy or internal energy, it is possible to obtain absolute entropy values by measuring the entropy change that occurs between the reference point of 0 K [corresponding to S = 0 J/(mol·K)] and 298 K.
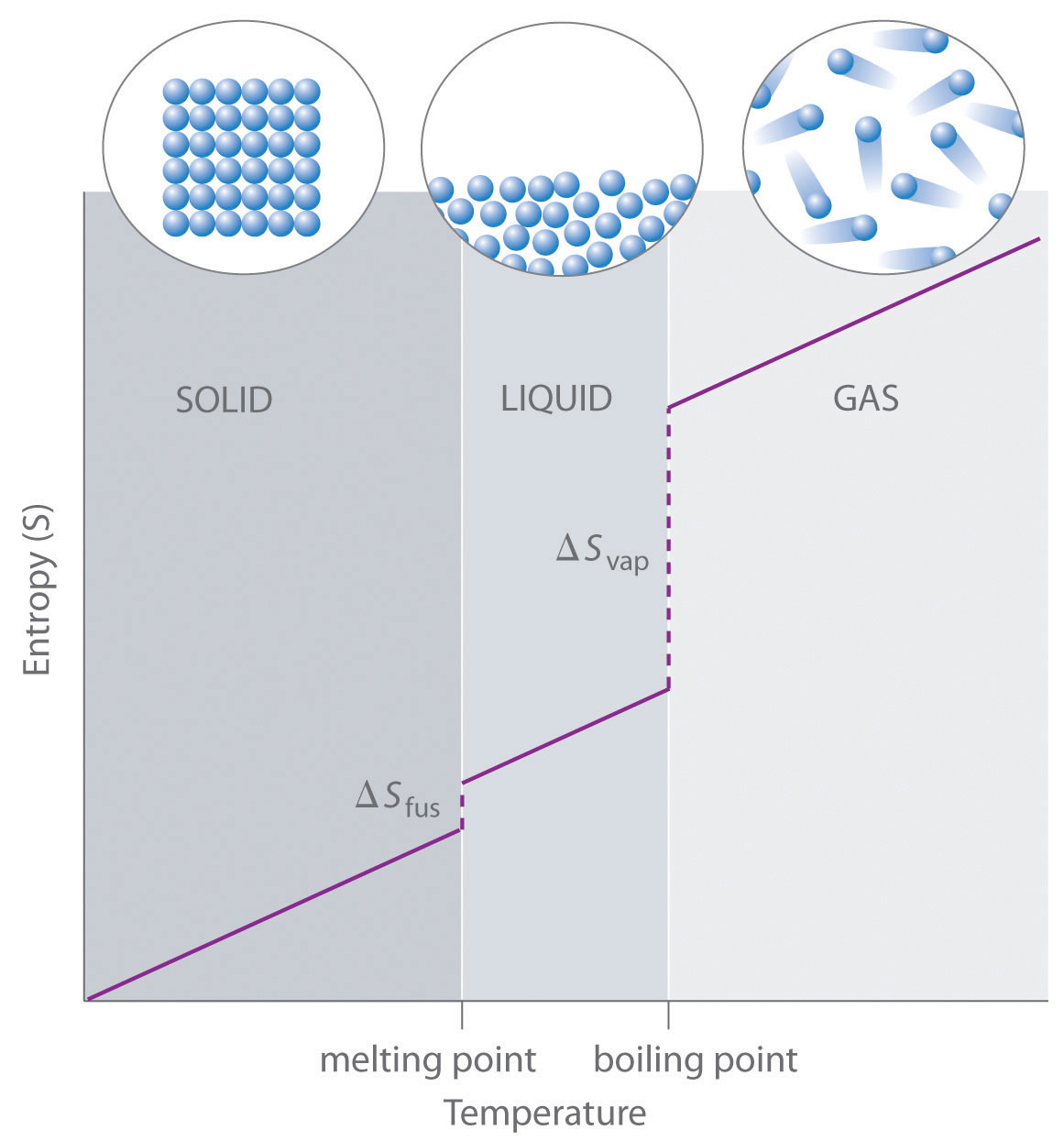
As shown in Table \(\PageIndex{1}\), for substances with approximately the same molar mass and number of atoms, S° values fall in the order S°(gas) > S°(liquid) > S°(solid). For instance, S° for liquid water is 70.0 J/(mol·K), whereas S° for water vapor is 188.8 J/(mol·K). Likewise, S° is 260.7 J/(mol·K) for gaseous I2 and 116.1 J/(mol·K) for solid I2. This order makes qualitative sense based on the kinds and extents of motion available to atoms and molecules in the three phases. The correlation between physical state and absolute entropy is illustrated in Figure \(\PageIndex{2}\), which is a generalized plot of the entropy of a substance versus temperature.
| Gases | Liquids | Solids | |||
|---|---|---|---|---|---|
| Substance | S° [J/(mol·K)] | Substance | S° [J/(mol·K)] | Substance | S° [J/(mol·K)] |
| He | 126.2 | H2O | 70.0 | C (diamond) | 2.4 |
| H2 | 130.7 | CH3OH | 126.8 | C (graphite) | 5.7 |
| Ne | 146.3 | Br2 | 152.2 | LiF | 35.7 |
| Ar | 154.8 | CH3CH2OH | 160.7 | SiO2 (quartz) | 41.5 |
| Kr | 164.1 | C6H6 | 173.4 | Ca | 41.6 |
| Xe | 169.7 | CH3COCl | 200.8 | Na | 51.3 |
| H2O | 188.8 | C6H12 (cyclohexane) | 204.4 | MgF2 | 57.2 |
| N2 | 191.6 | C8H18 (isooctane) | 329.3 | K | 64.7 |
| O2 | 205.2 | NaCl | 72.1 | ||
| CO2 | 213.8 | KCl | 82.6 | ||
| I2 | 260.7 | I2 | 116.1 | ||
Entropy increases with softer, less rigid solids, solids that contain larger atoms, and solids with complex molecular structures.
A closer examination of Table \(\PageIndex{1}\) also reveals that substances with similar molecular structures tend to have similar S° values. Among crystalline materials, those with the lowest entropies tend to be rigid crystals composed of small atoms linked by strong, highly directional bonds, such as diamond [S° = 2.4 J/(mol·K)]. In contrast, graphite, the softer, less rigid allotrope of carbon, has a higher S° [5.7 J/(mol·K)] due to more disorder in the crystal. Soft crystalline substances and those with larger atoms tend to have higher entropies because of increased molecular motion and disorder. Similarly, the absolute entropy of a substance tends to increase with increasing molecular complexity because the number of available microstates increases with molecular complexity. For example, compare the S° values for CH3OH(l) and CH3CH2OH(l). Finally, substances with strong hydrogen bonds have lower values of S°, which reflects a more ordered structure.
Entropy: Entropy(opens in new window) [youtu.be]
Summary
In general, the entropy is expected to increase for the following types of processes:
- The melting of a solid to form a liquid
- The vaporization of a liquid (or solid) to produce a gas
- Chemical reactions that involve phase changes of \(\text{solid} \rightarrow \text{liquid/gas}\), or \(\text{liquid} \rightarrow \text{gas}\)
- Chemical reactions that result in an increase in the number of gaseous molecules
- Any time the temperature of a substance is increased

