9.S: Molecular Geometry and Bonding Theories (Summary)
- Page ID
- 70549
9.1: Molecular Shapes
The Lewis electron-pair approach described previously can be used to predict the number and types of bonds between the atoms in a substance, and it indicates which atoms have lone pairs of electrons. This approach gives no information about the actual arrangement of atoms in space, however.
- Bond angles: angles made by the lines joining the nuclei of the atoms in a molecule
- Bond angles determine overall shape of molecule
VSEPR Model" data-cke-saved-href="/Bookshelves/General_Chemistry/Map:_Chemistry_-_The_Central_Science_(Brown_et_al.)/09:_Molecular_Geometry_and_Bonding_Theories/9.02:_The_VSEPR_Model" href="/Bookshelves/General_Chemistry/Map:_Chemistry_-_The_Central_Science_(Brown_et_al.)/09:_Molecular_Geometry_and_Bonding_Theories/9.02:_The_VSEPR_Model" data-quail-id="12">9.2: The VSEPR Model
The VSEPR model can predict the structure of nearly any molecule or polyatomic ion in which the central atom is a nonmetal, as well as the structures of many molecules and polyatomic ions with a central metal atom. The VSEPR model is not a theory; it does not attempt to explain observations. Instead, it is a counting procedure that accurately predicts the three-dimensional structures of a large number of compounds, which cannot be predicted using the Lewis electron-pair approach.
The Valence-Shell Electron Pair-Repulsion Model
- Valence-shell electron-pair repulsion (VSEPR) model: model that accounts for the geometric arrangements of shared and unshared electron pairs around a central atom in terms of the repulsions between electron pairs
- Electrons repel one another; hence, the best arrangement of a given number of electron pairs is the one that minimizes the repulsions among them.
Predicting Molecular Geometries
- Two types of valence-shell electron pairs; bonding pairs and nonbonding pairs.
- Electron-pair geometry: 3-D arrangement of electron pairs around an atom according to the VSEPR model
- Molecular geometry: the arrangement in space of the atoms of a molecule
When describing the shapes of molecules, we always give the molecular geometry rather than the electron-pair geometry. Molecular geometries only include BONDING pairs. For example, NH3 is a tetrahedral according to electron-pair geometry because it has 3 bonds and an unshared pair of electron. However, according to molecular geometry it is a trigonal pyramidal because it has only 3 bonds.
How to predict molecular geometries using VSEPR model:
- Sketch the Lewis dot structure of the molecule or ion
- Count the total number of electron pairs around the central atom and arrange them in the way that minimizes electron-pair repulsions
- Describe the molecular geometry in terms of the angular arrangement of the bonding pairs
Four or Fewer Valence-Shell Electron Pairs
A double or triple bond has essentially the same effect on bond angles as a single bond and is therefore counted as one bonding pair (that is, one electron region) when predicting geometry
The Effect of Nonbonding Electrons and Multiple Bonds on Bond Angles
Bond angles decrease as the number of nonbonding electron pairs increases. Bonding pairs are attracted by the two nuclei. By contrast, nonbonding electrons move under the attractive influence of only one nucleus and thus spread out more in space.
- Nonbonding electron pairs exert greater repulsive forces on adjacent electron pairs and thus tend to compress the angles between the bonding pairs
- Electrons in multiple bonds, like nonbonding pairs, exert a greater repulsive force on adjacent electron pairs than do single bonds.
Geometries of Molecules with Expanded Valence Shells
- When the central atom of a molecule or ion is from the third period of the periodic table and beyond (has d subshell) that atom may have more than four electron pairs around it
- The most stable electron-pair geometry for five electron pairs is the Trigonal bipyramid.
- Trigonal bipyramid geometries have two distinct types of electron pairs. They are axial pairs and equatorial pairs. In axial position, an electron pair is situated 90° from the three equatorial pairs. In an equatorial position, an electron pairs is situated 120° from the other two equatorial pairs and 90° from the two axial pairs.
- Because nonbonding pairs exert larger repulsions than bonding pairs, they always occupy the equatorial positions
- The most stable electron-pair geometry for six electron pairs is the octahedron.
- In an octahedron, the angles are either 90° or 180°, and all six positions are equivalent
Molecules with No Single Central Atom
Consider acetic acid molecule
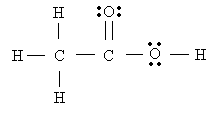
- Notice that the leftmost C has four bonded pairs around it. Hence, it must be a tetrahedral.
- The central C has 3 bonding pairs around it (counting the double bond as a single pair), hence, it is trigonal planar
- O has two bonding pairs, and two nonbonding ones. Hence, it is bent.
9.3: Molecular Shape and Molecular Polarity
Compounds with polar covalent bonds have electrons that are shared unequally between the bonded atoms. The polarity of such a bond is determined largely by the relative electronegativites of the bonded atoms. The asymmetrical charge distribution in a polar substance produces a dipole moment, which is the product of the partial charges on the bonded atoms and the distance between them.
Polar: in a molecule, if its centers of negative and positive charge don’t coincide, aka dipole
- If there are no charges on the opposite ends of a molecule, or if the charges have the same sign, the molecule does not have a dipole moment and is therefore nonpolar. Any diatomic molecule with a polar bond is a polar molecule
- Polar molecules align themselves with respect to one another. The negative end of a polar molecule is attracted to a positive ion, the positive end is attracted to a negative ion
- Dipole moment: measures the degree of polarity of a given molecule. The dipole moment, \(\mu\), is the product of the charge at either end of the dipole, \(Q\), times the distance, \(r\), between the charges.
\[\mu =Qr \nonumber \]
Therefore, the dipole moment increases as the quantity of charge that is separated increases and as the distance between the positive and negative centers increases. Dipole moments are generally reported in debyes (D), a unit equaling 3.33 X 10-30 C-m.
The Polarity of Polyatomic Molecules
- The polarity of a molecule containing more than two atoms depends on both the polarities of the bonds and the geometry of the molecule
- For each polar bond in a molecule, we can consider the bond dipole, that is, the dipole moment due only to the two atoms bonded together. We must then ask what the overall dipole moment results from adding up the individual bond dipoles. Let’s use CO2 (linear) as an example
- In CO2, each C – O bond is polar, and because they are identical, the bond dipoles are equal in magnitude.
- The fact that both C – O bonds are polar doesn’t necessarily mean the whole CO2 molecule is
- Bond dipoles and dipole moments are vector quantities; they have both a magnitude and direction. When calculating the overall dipole moment, both the magnitude and direction of the bond dipoles must be considered in this sum of vectors
- The two bond dipoles in CO2, although equal in magnitude, are opposite in direction, which makes them cancel each other out. Hence, CO2 has an overall dipole moment of zero. Even though the oxygen atoms in CO2 carry a partial negative charge, the geometry of the molecule dictates the overall dipole moment.
- Now, let’s consider H2O. Both of its bonds are identical once again, but the geometry is bent instead of linear. Hence, the bonds do not cancel each other out, and H2O has a dipole moment
- Molecules in which the central is symmetrically surrounded by identical atoms (BF3, CCl4) are nonpolar.
- For ABn molecules in which ALL of the B atoms are the same, certain symmetrical geometries – linear (AB2), trigonal planar (AB3), tetrahedral and square planar (AB4), trigonal bipyramidal (AB5), and octahedral (AB6) – must lead to nonpolar molecules, regardless of how polar the individual bonds are.
9.4: Covalent Bonding and Orbital Overlap
A more sophisticated treatment of bonding is needed for systems such as these. In this section, we present a quantum mechanical description of bonding, in which bonding electrons are viewed as being localized between the nuclei of the bonded atoms. The overlap of bonding orbitals is substantially increased through a process called hybridization, which results in the formation of stronger bonds.
Valence bond theory: model of chemical bonding in which an electron-pair bond is formed between two atoms by the overlap of orbitals on the two atoms
- Covalent bonding occurs when atoms share electrons. This increases the electron density between the two nuclei, and is visualized as occurring when a valence atomic orbital of one atom merges with that of another atom
- As the distance between the atoms decreases, their overlap increases. Because of the resultant increase in electron density between the nuclei, the potential energy of the system decreases, increasing the strength of the bond.
- The observed bond length is the distance at which the attractive forces between unlike charges (electrons and nuclei) are balanced by the repulsive forces between like charges (electron-electron and nucleus-nucleus)
9.5: Hybrid Orbitals
The localized valence bonding theory uses a process called hybridization, in which atomic orbitals that are similar in energy but not equivalent are combined mathematically to produce sets of equivalent orbitals that are properly oriented to form bonds. These new combinations are called hybrid atomic orbitals because they are produced by combining (hybridizing) two or more atomic orbitals from the same atom.
sp Hybrid Orbitals
- Use the salt BeF2 as an example. Its geometry is linear, however it is now hard to determine which orbitals on the Be atom overlap with those of the F atoms. The electron configuration of Be is 1s2 2s2. Hence, Be in its ground state has no unpaired electrons and is unable to form bonds
- Be’s only option is to "promote" one of its two electrons in the 2s shell to the 2p shell. It will then have a configuration of 1s2 2s1 2p1. Since the 2p orbital is at a higher energy level than the 2s orbital, this promotion requires energy
- The Be atom now has two unpaired electrons (2s and 2p) and would be able to form two bonds, which will not be similar. The two new orbitals are identical in shape (two lobes; one much larger than the other) but are oriented in different directions. Two hybrid orbitals have been created
- Hybrid orbitals: orbitals that result from the mixing of different kinds of atomic orbitals on the same atom. For example and sp3 hybrid results from the mixing, or hybridizing, of one s orbital and three p orbitals
- Hybridization: mixing of different types of atomic orbitals to produce a set of equivalent hybrid orbitals
- In this case, we have hybridized one s and one p orbital, so we call each hybrid an sp hybrid orbital. For the Be atom of BeF2, the orbital diagram is written as follows: 1s2 2sp2
- Hybrid orbitals have one large lobe and can therefore be directed at surrounding atoms more effectively, forming stronger bonds. The energy released by such bonds enables the promotion of a 2s electron to the 2p level.
sp2 and sp3 Hybrid Orbitals
- Whenever we mix a certain number of atomic orbitals, we get the same number of hybrid orbitals. Each of these hybrid orbitals is equivalent to the others but points in a different direction.
- Consider BF3. B has an electron configuration of 2s2 2p1. It promotes one of its 2s electron to the 2p orbital to have a configuration of 2s1 2p2. Then, it hybridizes into 3 sp2 hybrid orbitals
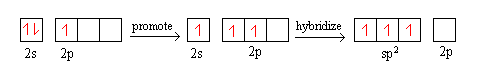
The same process can apply to the creation of sp3 hybrid orbitals
Hybridization Involving d Orbitals
Same process as sp2 orbitals. For example, mixing one s orbital, three p orbitals, and two d orbitals gives six sp3d2 hybrid orbitals, which are directed at the vertices of an octahedron
Section Summary
The molecular geometry needs to be known first in order to use the concept of hybridization, then we can use the following rules:
- Draw the Lewis structure for the molecule or ion
- Determine the electron-pair geometry using the VSEPR model
- Specify the hybrid orbitals needed to accommodate the electron pairs based on their geometrical arrangement
9.6: Multiple Bonds
To describe the bonding in more complex molecules with multiple bonds, we can use an approach that uses hybrid atomic orbitals to describe the σσ bonding and molecular orbitals to describe the \(π\) bonding. In this approach, unhybridized np orbitals on atoms bonded to one another are allowed to interact to produce bonding, antibonding, or nonbonding combinations.
In each covalent bond we have considered so far, the electron density is concentrated symmetrically about the line that connects the two nuclei (internuclear axis). This axis passes through the middle of the overlap region
- Sigma (σ) bond: covalent bond in which electron density is concentrated along the internuclear axis
- Pi (π) bond: covalent bond in which electron density is concentrated above and below the internuclear axis. Pi bonds are generally weaker than sigma bonds (less overlap)
Usually, single bonds are \(\sigma\) bonds. A double bond has one \(\sigma\) bond and one \(\pi\) bond. A triple bond has one \(\sigma\) bond and two \(\pi\) bonds.
Consider C2H4 as an example. After hybridization, C has 3 sp2 hybrid orbitals and one electron in the remaining unhybridized 2p orbital. The unhybridized 2p electron is directly perpendicular to the plane that contains the three sp2 hybrid orbitals
- The C – H \(\sigma\) bond is formed by the overlap of a sp2 hybrid orbital with the 1s orbital of hydrogen. Hence, the bond uses two electrons
- The C – C \(\sigma\) bond is formed by the overlap of two sp2 hybrid orbitals, one on each carbon atom, and requires two more electrons. Overall, C2H4 has 12 valence electrons, 10 of which are used in the formation of the bonds
- The remaining two valence electrons reside in the unhybridized 2p orbitals, one electron on each of the atoms
- The 2p orbitals can overlap with one another in a sideways fashion. This will lead to the electron density being concentrated above and below the C – C bond axis, hence being a \(\pi\) bond
Because \(\pi\) bonds require that portions of a molecule be planar, they can introduce rigidity into molecules (strongly affects the properties of substances)
Although \(\pi\) bonds can be formed from d orbitals, we will only consider those formed by p orbitals. They can only form if unhybridized p orbitals are present on the bonded atoms. Only atoms having sp or sp2 hybridization can be involved in \(\pi\) bonding. Double and triple bonds are more common in molecules with small atoms
Delocalized Bonding
- σ and \(\pi\) electrons are localized when they are associated totally with two atoms forming the bond.
- In some molecules, particularly those with more than one resonance form, we cannot accurately describe the bonding as localized. In order to deal with this, we "smear out" the bonds (delocalize them) so that it fits both resonance structures as best as possible
Delocalized electrons: electrons that are spread over a number of atoms in a molecule rather than localized between a pair of atoms
Section Summary
- Every pair of bonded atoms shares one or more pairs of electrons. In every bond, at least one pair of electrons is localized in the space between the atoms, in a \(\sigma\) bond. The appropriate set of hybrid orbitals used to form the \(\sigma\) bonds between an atom and its neighbors is determined by the observed geometry of the molecule
- The electrons in \(\sigma\) bonds are localized in the region between two bonded atoms and do not make a significant contributions to the bonding between any other two atoms
- When atoms share more than one pair of electrons, the additional pairs are in \(\pi\) bonds. The centers of chare density in a \(\pi\) bond lie above an below the bond axis.
- Molecules with two or more resonance forms can have \(\pi\) bonds that extend over more than two bonded atoms. Electrons in \(\pi\) bonds that extend over more than two bonded atoms are said to be delocalized
9.7: Molecular Orbitals
A molecular orbital is an allowed spatial distribution of electrons in a molecule that is associated with a particular orbital energy. Unlike an atomic orbital, which is centered on a single atom, a molecular orbital extends over all the atoms in a molecule or ion. Hence the molecular orbital theory of bonding is a delocalized approach. Molecular orbitals are constructed using linear combinations of atomic orbitals (LCAOs), which describe overlapping atomic orbitals.
- Molecular orbital theory: theory that predicts that electrons in molecules exist in allowed energy states.
- Molecular orbitals: allowed state for an electron in a molecule. Molecular orbitals are very similar to atomic orbitals. Both hold a maximum of two electrons (with opposite spins), have definite energies, and their electron-density distribution can be visualized by using contour representations. However, molecular orbitals are associated with the entire molecule
The Hydrogen Molecule
Consider H2 as an example. Whenever two atomic orbitals overlap, two molecular orbitals form. Thus, the overlap of the 1s orbitals of two hydrogen atoms to form H2 produces two molecular orbitals.
Bonding molecular orbital: molecular orbital in which the electron density is concentrated in the internuclear region. The energy of a bonding molecular orbital is lower than the energy of the separate atomic orbitals from which it forms.
The bonding molecular orbital results from summing the two atomic orbitals so that the atomic orbital wave functions enhance each other in the bond region. Because an electron in this molecular orbital is strongly attracted to both nuclei, the electron is more stable (lower energy) than it is in the 1s orbital of hydrogen. Because it concentrates electron density between both nuclei, the bonding molecular orbital holds the atoms together in a covalent bond.
Antibonding molecular orbital: molecular orbital in which electron density is concentrated outside the region between the two nuclei of bonded atoms. Such orbitals, designated as σ* or π*, are less stable (of higher energy) than bonding molecular orbitals
- An electron in the antibonding molecular orbital is repelled from the bonding region and is therefore less stable (higher energy) than it is in the 1s orbital of the hydrogen atom
- Sigma (σ) molecular orbital: molecular orbital that centers the electron density about an imaginary line passing through two nuclei
- Energy level diagram: aka Molecular orbital diagram; diagram that shows the energies of molecular orbitals relative to the atomic orbitals from which they are derived
- Electrons occupying a bonding molecular orbital are called bonding electrons
Bond Order
- Bond order: related to the stability of a covalent bond.
\[\text{Bond order} = \dfrac{1}{2} (\text{number of bonding electrons – number of antibonding electrons})\nonumber \]
A bond order of 1 represents a single bond, a bond order of 2 represents a double bond, and a bond order of 3 represents a triple bond. A bond order of 0 means that no bonds exist
9.8: Second-Row Diatomic Molecules
Molecular orbital energy-level diagrams for diatomic molecules can be created if the electron configuration of the parent atoms is known, following a few simple rules. Most important, the number of molecular orbitals in a molecule is the same as the number of atomic orbitals that interact. The difference between bonding and antibonding molecular orbital combinations is proportional to the overlap of the parent orbitals and decreases as the energy difference between the atomic orbitals increases.
Material here applies to homonuclear diatomic molecules (those composed of identical atoms)
- The number of atomic orbitals formed equals the number of atomic orbitals combined
- Atomic orbitals combine most effectively with other atomic orbitals of similar energy
- The effectiveness with which two atomic orbitals combine is proportional to their overlap with one another; that is, as the overlap increases, the bonding orbital is lowered in energy, and the antibonding orbital is raised in energy
- Each molecular orbital can accommodate at most two electrons, with their spins paired (Pauli exclusion principle)
- When molecular orbitals have the same energy, one electron enters each orbital (with parallel spins) before spin pairing occurs (Hund’s rule)
Molecular Orbitals for Li2 and Be2
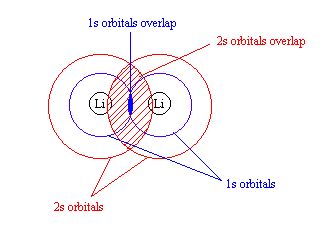
- Lithium has 1s and 2s orbitals, but both are extremely different. According to the Lewis structure of Li2, there is a single Li – Li bond.
- Because the 1s and 2s orbitals are so different in energy, it is likely that the 1s orbitals interact with each other. (See rule 2)
- This would create a much larger overlap between the 2s orbitals (see figure)
- As a result, the energy seperation between the σ2s and σ*2s is greater than that for the 1s-based orbitals.
- Each Li atom has 3 electrons; so six electrons must be placed in the molecular orbitals of Li2
- The electrons occupy the σ1s , σ*1s , and σ2s orbitals (not the σ*2s orbital). There are 4 bonding orbitals and 2 nonbonding ones, so the bond order equals ½ (4 – 2) = 1. The molecule has a single bond, in accord with its Lewis structure.
Filled atomic subshells usually do not contribute significantly to bonding in molecule formation
In Be2, each Be has 4 electrons, for a total of eight. When we place them in molecular orbitals, we fill the σ1s , σ*1s , σ2s , and σ*2s orbitals. There is an equal number of bonding and antibonding electrons, so the bond order is 0. Thus, Be2 doesn’t exist.
Molecular Orbitals from 2p Atomic Orbitals
- z axis is internuclear axis (in this example). 2pz orbitals face each other in a "head-to-head" fashion along the z-axis. They combine like the s orbitals, with one combination concentrating electron density between both nuclei, and the other excluding the electron density from the bonding region. In each of these combinations, the electron density lies along the internuclear axis. Hence, they are σ molecular orbitals: σ2p and σ*2p
- The other 2p orbitals overlap in a sideways fashion and thus concentrate electron density on opposite sides of the internuclear axis. Molecular orbitals of this type are called pi molecular orbitals . We get two π2p molecular orbitals by combining 2px and 2py molecular orbitals. The resulting π2p molecular orbitals are degenerate (same energy). Likewise, two degenerate π*2p antibonding molecular orbitals are formed.
- The 2pz orbitals on two atoms point directly at one another, hence, having a greater overlap than the 2px and 2py orbitals. From rule 3, we can expect the σ2p molecular orbital to be lower in energy (more stable) tha n the π2p molecular orbitals.
Electron Configurations for B2 Through F2
- The elements Boron through Fluorine all have 2s and 2p valence electrons
- In the energy diagram, the σ2p molecular orbital is at higher energy than the π2p molecular orbitals, contrary to what we would expect from rule 3.
- This is because of interaction between the σ2s and σ2p molecular orbitals. It results in the σ2p molecular orbital being pushed upward in energy to the point where it is above the π2p orbi tals, and the σ2s molecular orbital is pushed down in energy. (The interaction between σ 2p and σ 2s molecular orbitals decreases as we move from left to right in the second period. As a result, the σ 2p is higher in energy than the π 2p orbitals for B2, C2, and N2. For O2, F2, and Ne2 , the σ 2p orbital is lower in energy than the π 2p orbitals)
- Boron has 3 valence electrons. Thus, for B2, we must place 6 electrons in molecular orbitals. Four of these occupy the σ2s and σ*2s molecular orbitals, leading to no net bonding. The last two electrons are put in the π2p bonding molecular orbitals; one electron is put in each π2p molecular orbital with the same spin (rule 5). Therefore, B2 has a bond order of 1.
Electron Configurations and Molecular Properties
- Molecules with one or more unpaired electrons are attracted into a magnetic field. The more unpaired electrons, the stronger the force of the attraction
- Paramagnetism: property that a substance possesses if it contains one or more unpaired electrons. A paramagnetic substance is drawn into a magnetic field
- Diamagnetism: type of magnetism that causes a substance with no unpaired electrons to be weakly repelled from a magnetic field.
- Diamagnetism is a much weaker effect than paramagnetism
- As bond orders increase, bond distances decrease and bond-dissociation energies increase.
- Molecules with the same bond order do not have the same bond distances and bond-dissociation energies. There are other factors involved, such as nuclear charges and the extend of orbital overlap.
Callstack:
at (Bookshelves/General_Chemistry/Map:_Chemistry_-_The_Central_Science_(Brown_et_al.)/09:_Molecular_Geometry_and_Bonding_Theories/9.S:_Molecular_Geometry_and_Bonding_Theories_(Summary)), /content/body/div[7]/p[9]/span, line 1, column 19

