8.6: Resonance Structures
- Page ID
- 21750
- To understand the concept of resonance.
Resonance structures are a set of two or more Lewis Structures that collectively describe the electronic bonding of a single polyatomic species including fractional bonds and fractional charges. Resonance structures are capable of describing delocalized electrons that cannot be expressed by a single Lewis formula with an integral number of covalent bonds.
Sometimes one Lewis Structure is not Enough
Sometimes, even when formal charges are considered, the bonding in some molecules or ions cannot be described by a single Lewis structure. Resonance is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by a single Lewis formula. A molecule or ion with such delocalized electrons is represented by several contributing structures (also called resonance structures or canonical forms). Such is the case for ozone (\(\ce{O3}\)), an allotrope of oxygen with a V-shaped structure and an O–O–O angle of 117.5°.
Ozone (\(O_3\))
1. We know that ozone has a V-shaped structure, so one O atom is central:

2. Each O atom has 6 valence electrons, for a total of 18 valence electrons.
3. Assigning one bonding pair of electrons to each oxygen–oxygen bond gives

with 14 electrons left over.
4. If we place three lone pairs of electrons on each terminal oxygen, we obtain

and have 2 electrons left over.
5. At this point, both terminal oxygen atoms have octets of electrons. We therefore place the last 2 electrons on the central atom:

6. The central oxygen has only 6 electrons. We must convert one lone pair on a terminal oxygen atom to a bonding pair of electrons—but which one? Depending on which one we choose, we obtain either
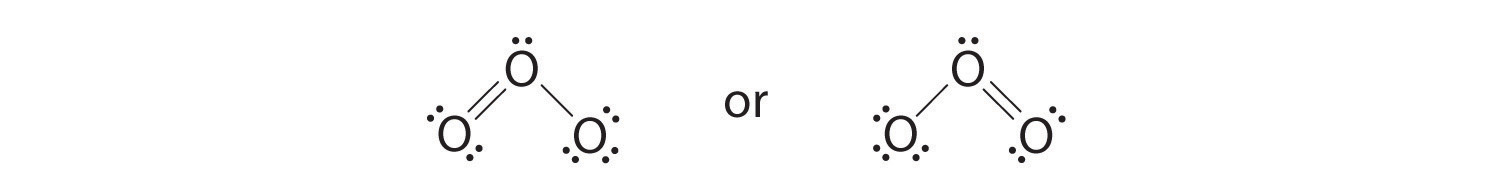
Which is correct? In fact, neither is correct. Both predict one O–O single bond and one O=O double bond. As you will learn, if the bonds were of different types (one single and one double, for example), they would have different lengths. It turns out, however, that both O–O bond distances are identical, 127.2 pm, which is shorter than a typical O–O single bond (148 pm) and longer than the O=O double bond in O2 (120.7 pm).
Equivalent Lewis dot structures, such as those of ozone, are called resonance structures. The position of the atoms is the same in the various resonance structures of a compound, but the position of the electrons is different. Double-headed arrows link the different resonance structures of a compound:

The double-headed arrow indicates that the actual electronic structure is an average of those shown, not that the molecule oscillates between the two structures.
When it is possible to write more than one equivalent resonance structure for a molecule or ion, the actual structure is the average of the resonance structures.
The Carbonate (\(CO_3^{2−} \)) Ion
Like ozone, the electronic structure of the carbonate ion cannot be described by a single Lewis electron structure. Unlike O3, though, the actual structure of CO32− is an average of three resonance structures.
1. Because carbon is the least electronegative element, we place it in the central position:
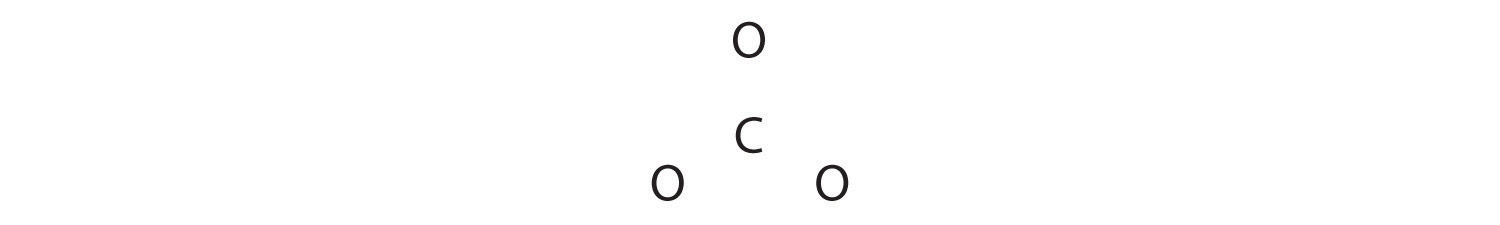
2. Carbon has 4 valence electrons, each oxygen has 6 valence electrons, and there are 2 more for the −2 charge. This gives 4 + (3 × 6) + 2 = 24 valence electrons.
3. Six electrons are used to form three bonding pairs between the oxygen atoms and the carbon:

4. We divide the remaining 18 electrons equally among the three oxygen atoms by placing three lone pairs on each and indicating the −2 charge:

5. No electrons are left for the central atom.
6. At this point, the carbon atom has only 6 valence electrons, so we must take one lone pair from an oxygen and use it to form a carbon–oxygen double bond. In this case, however, there are three possible choices:
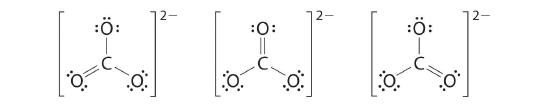
As with ozone, none of these structures describes the bonding exactly. Each predicts one carbon–oxygen double bond and two carbon–oxygen single bonds, but experimentally all C–O bond lengths are identical. We can write resonance structures (in this case, three of them) for the carbonate ion:
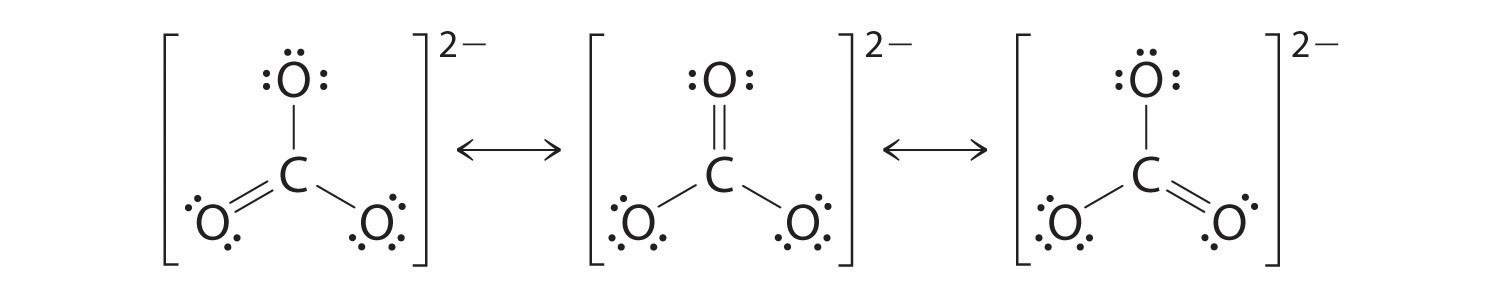
The actual structure is an average of these three resonance structures.
The Nitrate (\(NO_3^-\)) ion
1. Count up the valence electrons: (1*5) + (3*6) + 1(ion) = 24 electrons
2. Draw the bond connectivities:
3. Add octet electrons to the atoms bonded to the center atom:
4. Place any leftover electrons (24-24 = 0) on the center atom:
5. Does the central atom have an octet?
- NO, it has 6 electrons
- Add a multiple bond (first try a double bond) to see if the central atom can achieve an octet:
6. Does the central atom have an octet?
- YES
- Are there possible resonance structures? YES
Note: We would expect that the bond lengths in the \(\ce{NO_3^{-}}\) ion to be somewhat shorter than a single bond.
Benzene is a common organic solvent that was previously used in gasoline; it is no longer used for this purpose, however, because it is now known to be a carcinogen. The benzene molecule (\(\ce{C6H6}\)) consists of a regular hexagon of carbon atoms, each of which is also bonded to a hydrogen atom. Use resonance structures to describe the bonding in benzene.
Given: molecular formula and molecular geometry
Asked for: resonance structures
Strategy:
- Draw a structure for benzene illustrating the bonded atoms. Then calculate the number of valence electrons used in this drawing.
- Subtract this number from the total number of valence electrons in benzene and then locate the remaining electrons such that each atom in the structure reaches an octet.
- Draw the resonance structures for benzene.
Solution:
A Each hydrogen atom contributes 1 valence electron, and each carbon atom contributes 4 valence electrons, for a total of (6 × 1) + (6 × 4) = 30 valence electrons. If we place a single bonding electron pair between each pair of carbon atoms and between each carbon and a hydrogen atom, we obtain the following:
Each carbon atom in this structure has only 6 electrons and has a formal charge of +1, but we have used only 24 of the 30 valence electrons.
B If the 6 remaining electrons are uniformly distributed pairwise on alternate carbon atoms, we obtain the following:
Three carbon atoms now have an octet configuration and a formal charge of −1, while three carbon atoms have only 6 electrons and a formal charge of +1. We can convert each lone pair to a bonding electron pair, which gives each atom an octet of electrons and a formal charge of 0, by making three C=C double bonds.
C There are, however, two ways to do this:
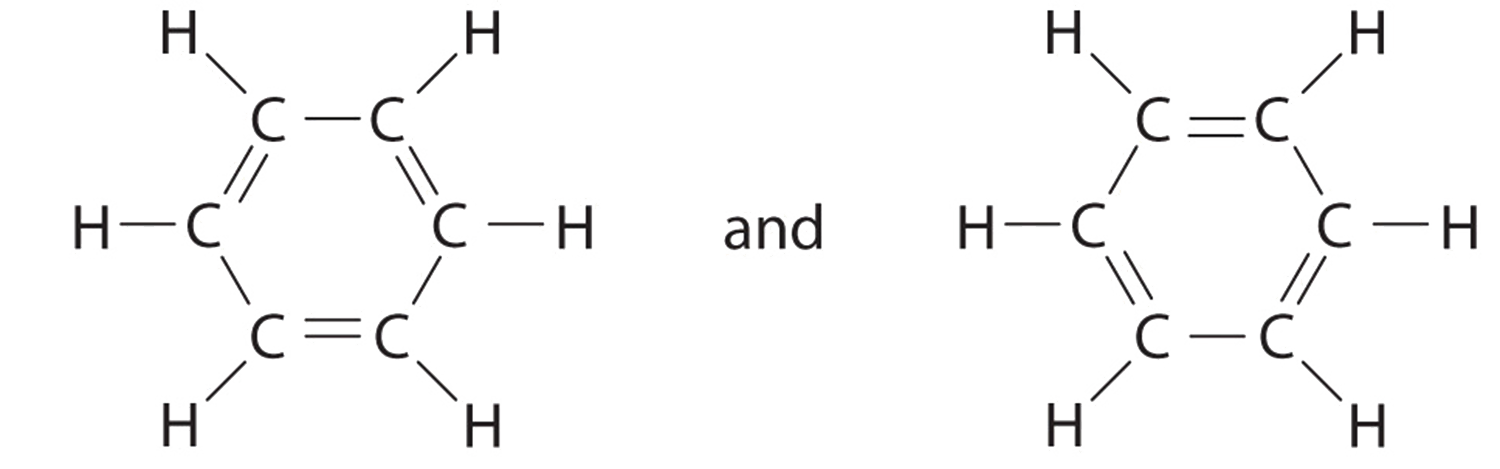
Each structure has alternating double and single bonds, but experimentation shows that each carbon–carbon bond in benzene is identical, with bond lengths (139.9 pm) intermediate between those typically found for a C–C single bond (154 pm) and a C=C double bond (134 pm). We can describe the bonding in benzene using the two resonance structures, but the actual electronic structure is an average of the two. The existence of multiple resonance structures for aromatic hydrocarbons like benzene is often indicated by drawing either a circle or dashed lines inside the hexagon:
The sodium salt of nitrite is used to relieve muscle spasms. Draw two resonance structures for the nitrite ion (NO2−).
- Answer
-
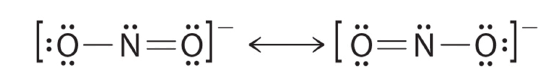
There is a double bond between one oxygen and the nitrogen, It can be found on the left oxygen or the right oxygen. Resonance structures are particularly common in oxoanions of the p-block elements, such as sulfate and phosphate, and in aromatic hydrocarbons, such as benzene and naphthalene.
If several reasonable resonance forms for a molecule exists, the "actual electronic structure" of the molecule will probably be intermediate between all the forms that you can draw. The classic example is benzene in Example \(\PageIndex{1}\). One would expect the double bonds to be shorter than the single bonds, but if one overlays the two structures, you see that one structure has a single bond where the other structure has a double bond. The best measurements that we can make of benzene do not show two bond lengths - instead, they show that the bond length is intermediate between the two resonance structures.
Resonance structures is a mechanism that allows us to use all of the possible resonance structures to try to predict what the actual form of the molecule would be. Single bonds, double bonds, triple bonds, +1 charges, -1 charges, these are our limitations in explaining the structures, and the true forms can be in between - a carbon-carbon bond could be mostly single bond with a little bit of double bond character and a partial negative charge, for example.
Summary
Some molecules have two or more chemically equivalent Lewis electron structures, called resonance structures. Resonance is a mental exercise and method within the Valence Bond Theory of bonding that describes the delocalization of electrons within molecules. These structures are written with a double-headed arrow between them, indicating that none of the Lewis structures accurately describes the bonding but that the actual structure is an average of the individual resonance structures. Resonance structures are used when one Lewis structure for a single molecule cannot fully describe the bonding that takes place between neighboring atoms relative to the empirical data for the actual bond lengths between those atoms. The net sum of valid resonance structures is defined as a resonance hybrid, which represents the overall delocalization of electrons within the molecule. A molecule that has several resonance structures is more stable than one with fewer. Some resonance structures are more favorable than others.

