13.2: Saturated Solutions and Solubility
- Page ID
- 21785
- To understand the relationship between solubility and molecular structure.
- To demonstrate how the strength of intramolecular bonding determines the solubility of a solute in a given solvent.
When a solute dissolves, its individual atoms, molecules, or ions interact with the solvent, become solvated, and are able to diffuse independently throughout the solution (Figure \(\PageIndex{1a}\)). This is not, however, a unidirectional process. If the molecule or ion happens to collide with the surface of a particle of the undissolved solute, it may adhere to the particle in a process called crystallization. Dissolution and crystallization continue as long as excess solid is present, resulting in a dynamic equilibrium analogous to the equilibrium that maintains the vapor pressure of a liquid. We can represent these opposing processes as follows:
\[ solute + solvent \underset{crystallization}{\stackrel{dissolution}{\longrightleftharpoons}} solution \nonumber \]
Although the terms precipitation and crystallization are both used to describe the separation of solid solute from a solution, crystallization refers to the formation of a solid with a well-defined crystalline structure, whereas precipitation refers to the formation of any solid phase, often one with very small particles.

Factors Affecting Solubility
The maximum amount of a solute that can dissolve in a solvent at a specified temperature and pressure is its solubility. Solubility is often expressed as the mass of solute per volume (g/L) or mass of solute per mass of solvent (g/g), or as the moles of solute per volume (mol/L). Even for very soluble substances, however, there is usually a limit to how much solute can dissolve in a given quantity of solvent. In general, the solubility of a substance depends on not only the energetic factors we have discussed but also the temperature and, for gases, the pressure. At 20°C, for example, 177 g of NaI, 91.2 g of NaBr, 35.9 g of NaCl, and only 4.1 g of NaF dissolve in 100 g of water. At 70°C, however, the solubilities increase to 295 g of NaI, 119 g of NaBr, 37.5 g of NaCl, and 4.8 g of NaF. As you learned in Chapter 12, the lattice energies of the sodium halides increase from NaI to NaF. The fact that the solubilities decrease as the lattice energy increases suggests that the \(ΔH_2\) term in Figure 13.1 dominates for this series of compounds.
A solution with the maximum possible amount of solute is saturated. If a solution contains less than the maximum amount of solute, it is unsaturated. When a solution is saturated and excess solute is present, the rate of dissolution is exactly equal to the rate of crystallization (Figure \(\PageIndex{1b}\)). Using the value just stated, a saturated aqueous solution of NaCl, for example, contains 35.9 g of NaCl per 100 mL of water at 20°C. We can prepare a homogeneous saturated solution by adding excess solute (in this case, greater than 35.9 g of NaCl) to the solvent (water), stirring until the maximum possible amount of solute has dissolved, and then removing undissolved solute by filtration.
The solubility of most solids increases with increasing temperature.
Because the solubility of most solids increases with increasing temperature, a saturated solution that was prepared at a higher temperature usually contains more dissolved solute than it would contain at a lower temperature. When the solution is cooled, it can therefore become supersaturated (Figure \(\PageIndex{1c}\)). Like a supercooled or superheated liquid, a supersaturated solution is unstable. Consequently, adding a small particle of the solute, a seed crystal, will usually cause the excess solute to rapidly precipitate or crystallize, sometimes with spectacular results. The rate of crystallization in Equation \(\ref{13.2.1}\) is greater than the rate of dissolution, so crystals or a precipitate form (Figure \(\PageIndex{1d}\)). In contrast, adding a seed crystal to a saturated solution reestablishes the dynamic equilibrium, and the net quantity of dissolved solute no longer changes.
Video \(\PageIndex{1}\): hot ice (sodium acetate) beautiful science experiment. watered-down sodium acetate trihydrate. Needle crystal is truly wonderful structures
Because crystallization is the reverse of dissolution, a substance that requires an input of heat to form a solution (\(ΔH_{soln} > 0\)) releases that heat when it crystallizes from solution (\(ΔH_{crys} < 0\)). The amount of heat released is proportional to the amount of solute that exceeds its solubility. Two substances that have a positive enthalpy of solution are sodium thiosulfate (\(Na_2S_2O_3\)) and sodium acetate (\(CH_3CO_2Na\)), both of which are used in commercial hot packs, small bags of supersaturated solutions used to warm hands (see Figure 13.1.3).
Interactions in Liquid Solutions
The interactions that determine the solubility of a substance in a liquid depend largely on the chemical nature of the solute (such as whether it is ionic or molecular) rather than on its physical state (solid, liquid, or gas). We will first describe the general case of forming a solution of a molecular species in a liquid solvent and then describe the formation of a solution of an ionic compound.
Solutions of Molecular Substances in Liquids
The London dispersion forces, dipole–dipole interactions, and hydrogen bonds that hold molecules to other molecules are generally weak. Even so, energy is required to disrupt these interactions. As described in Section 13.1, unless some of that energy is recovered in the formation of new, favorable solute–solvent interactions, the increase in entropy on solution formation is not enough for a solution to form.
For solutions of gases in liquids, we can safely ignore the energy required to separate the solute molecules (\(ΔH_2 = 0\)) because the molecules are already separated. Thus we need to consider only the energy required to separate the solvent molecules (\(ΔH_1\)) and the energy released by new solute–solvent interactions (\(ΔH_3\)). Nonpolar gases such as \(N_2\), \(O_2\), and \(Ar\) have no dipole moment and cannot engage in dipole–dipole interactions or hydrogen bonding. Consequently, the only way they can interact with a solvent is by means of London dispersion forces, which may be weaker than the solvent–solvent interactions in a polar solvent. It is not surprising, then, that nonpolar gases are most soluble in nonpolar solvents. In this case, \(ΔH_1\) and \(ΔH_3\) are both small and of similar magnitude. In contrast, for a solution of a nonpolar gas in a polar solvent, \(ΔH_1\) is far greater than \(ΔH_3\). As a result, nonpolar gases are less soluble in polar solvents than in nonpolar solvents. For example, the concentration of \(N_2\) in a saturated solution of \(N_2\) in water, a polar solvent, is only \(7.07 \times 10^{-4}\; M\) compared with \(4.5 \times 10^{-3}\; M\) for a saturated solution of \(N_2\) in benzene, a nonpolar solvent.
The solubilities of nonpolar gases in water generally increase as the molecular mass of the gas increases, as shown in Table \(\PageIndex{1}\). This is precisely the trend expected: as the gas molecules become larger, the strength of the solvent–solute interactions due to London dispersion forces increases, approaching the strength of the solvent–solvent interactions.
| Gas | Solubility (M) × 10−4 |
|---|---|
| He | 3.90 |
| Ne | 4.65 |
| Ar | 15.2 |
| Kr | 27.9 |
| Xe | 50.2 |
| H2 | 8.06 |
| N2 | 7.07 |
| CO | 10.6 |
| O2 | 13.9 |
| N2O | 281 |
| CH4 | 15.5 |
Virtually all common organic liquids, whether polar or not, are miscible. The strengths of the intermolecular attractions are comparable; thus the enthalpy of solution is expected to be small (\(ΔH_{soln} \approx 0\)), and the increase in entropy drives the formation of a solution. If the predominant intermolecular interactions in two liquids are very different from one another, however, they may be immiscible. For example, organic liquids such as benzene, hexane, \(CCl_4\), and \(CS_2\) (S=C=S) are nonpolar and have no ability to act as hydrogen bond donors or acceptors with hydrogen-bonding solvents such as \(H_2O\), \(HF\), and \(NH_3\); hence they are immiscible in these solvents. When shaken with water, they form separate phases or layers separated by an interface (Figure \(\PageIndex{2}\)), the region between the two layers.

Just because two liquids are immiscible, however, does not mean that they are completely insoluble in each other. For example, 188 mg of benzene dissolves in 100 mL of water at 23.5°C. Adding more benzene results in the separation of an upper layer consisting of benzene with a small amount of dissolved water (the solubility of water in benzene is only 178 mg/100 mL of benzene). The solubilities of simple alcohols in water are given in Table \(\PageIndex{2}\).
| Alcohol | Solubility (mol/100 g of \(H_2O\)) |
|---|---|
| methanol | completely miscible |
| ethanol | completely miscible |
| n-propanol | completely miscible |
| n-butanol | 0.11 |
| n-pentanol | 0.030 |
| n-hexanol | 0.0058 |
| n-heptanol | 0.0008 |
Only the three lightest alcohols (methanol, ethanol, and n-propanol) are completely miscible with water. As the molecular mass of the alcohol increases, so does the proportion of hydrocarbon in the molecule. Correspondingly, the importance of hydrogen bonding and dipole–dipole interactions in the pure alcohol decreases, while the importance of London dispersion forces increases, which leads to progressively fewer favorable electrostatic interactions with water. Organic liquids such as acetone, ethanol, and tetrahydrofuran are sufficiently polar to be completely miscible with water yet sufficiently nonpolar to be completely miscible with all organic solvents.
The same principles govern the solubilities of molecular solids in liquids. For example, elemental sulfur is a solid consisting of cyclic \(S_8\) molecules that have no dipole moment. Because the \(S_8\) rings in solid sulfur are held to other rings by London dispersion forces, elemental sulfur is insoluble in water. It is, however, soluble in nonpolar solvents that have comparable London dispersion forces, such as \(CS_2\) (23 g/100 mL). In contrast, glucose contains five –OH groups that can form hydrogen bonds. Consequently, glucose is very soluble in water (91 g/120 mL of water) but essentially insoluble in nonpolar solvents such as benzene. The structure of one isomer of glucose is shown here.

Low-molecular-mass hydrocarbons with highly electronegative and polarizable halogen atoms, such as chloroform (\(CHCl_3\)) and methylene chloride (\(CH_2Cl_2\)), have both significant dipole moments and relatively strong London dispersion forces. These hydrocarbons are therefore powerful solvents for a wide range of polar and nonpolar compounds. Naphthalene, which is nonpolar, and phenol (\(C_6H_5OH\)), which is polar, are very soluble in chloroform. In contrast, the solubility of ionic compounds is largely determined not by the polarity of the solvent but rather by its dielectric constant, a measure of its ability to separate ions in solution, as you will soon see.
Identify the most important solute–solvent interactions in each solution.
- iodine in benzene solvent
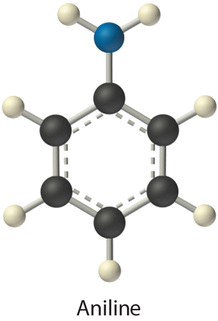
- aniline (\(\ce{C_6H_5NH_2}\)) in dichloromethane (\(\ce{CH_2Cl_2}\)) solvent
- iodine in water solvent
Given: components of solutions
Asked for: predominant solute–solvent interactions
Strategy:
Identify all possible intermolecular interactions for both the solute and the solvent: London dispersion forces, dipole–dipole interactions, or hydrogen bonding. Determine which is likely to be the most important factor in solution formation.
Solution
- Benzene and \(\ce{I2}\) are both nonpolar molecules. The only possible attractive forces are London dispersion forces.
- Aniline is a polar molecule with a dipole moment of 1.6 D and has an \(\ce{–NH_2}\) group that can act as a hydrogen bond donor. Dichloromethane is also polar with a 1.5 D dipole moment, but it has no obvious hydrogen bond acceptor. Therefore, the most important interactions between aniline and \(CH_2Cl_2\) are likely to be dipole-dipole interactions.
- Water is a highly polar molecule that engages in extensive hydrogen bonding, whereas \(I_2\) is a nonpolar molecule that cannot act as a hydrogen bond donor or acceptor. The slight solubility of \(\ce{I_2}\) in water (\(1.3 \times 10^{-3}\; mol/L\) at 25°C) is due to London dispersion forces.
Identify the most important interactions in each solution:
- ethylene glycol (\(HOCH_2CH_2OH\)) in acetone
- acetonitrile (\(\ce{CH_3C≡N}\)) in acetone
- n-hexane in benzene
- Answer a
-
hydrogen bonding
- Answer b
-
London interactions
- Answer c
-
London dispersion forces
Hydrophilic and Hydrophobic Solutes
A solute can be classified as hydrophilic (literally, “water loving”), meaning that it has an electrostatic attraction to water, or hydrophobic (“water fearing”), meaning that it repels water. A hydrophilic substance is polar and often contains O–H or N–H groups that can form hydrogen bonds to water. For example, glucose with its five O–H groups is hydrophilic. In contrast, a hydrophobic substance may be polar but usually contains C–H bonds that do not interact favorably with water, as is the case with naphthalene and n-octane. Hydrophilic substances tend to be very soluble in water and other strongly polar solvents, whereas hydrophobic substances are essentially insoluble in water and soluble in nonpolar solvents such as benzene and cyclohexane.
The difference between hydrophilic and hydrophobic substances has substantial consequences in biological systems. For example, vitamins can be classified as either fat soluble or water soluble. Fat-soluble vitamins, such as vitamin A, are mostly nonpolar, hydrophobic molecules. As a result, they tend to be absorbed into fatty tissues and stored there. In contrast, water-soluble vitamins, such as vitamin C, are polar, hydrophilic molecules that circulate in the blood and intracellular fluids, which are primarily aqueous. Water-soluble vitamins are therefore excreted much more rapidly from the body and must be replenished in our daily diet. A comparison of the chemical structures of vitamin A and vitamin C quickly reveals why one is hydrophobic and the other hydrophilic.
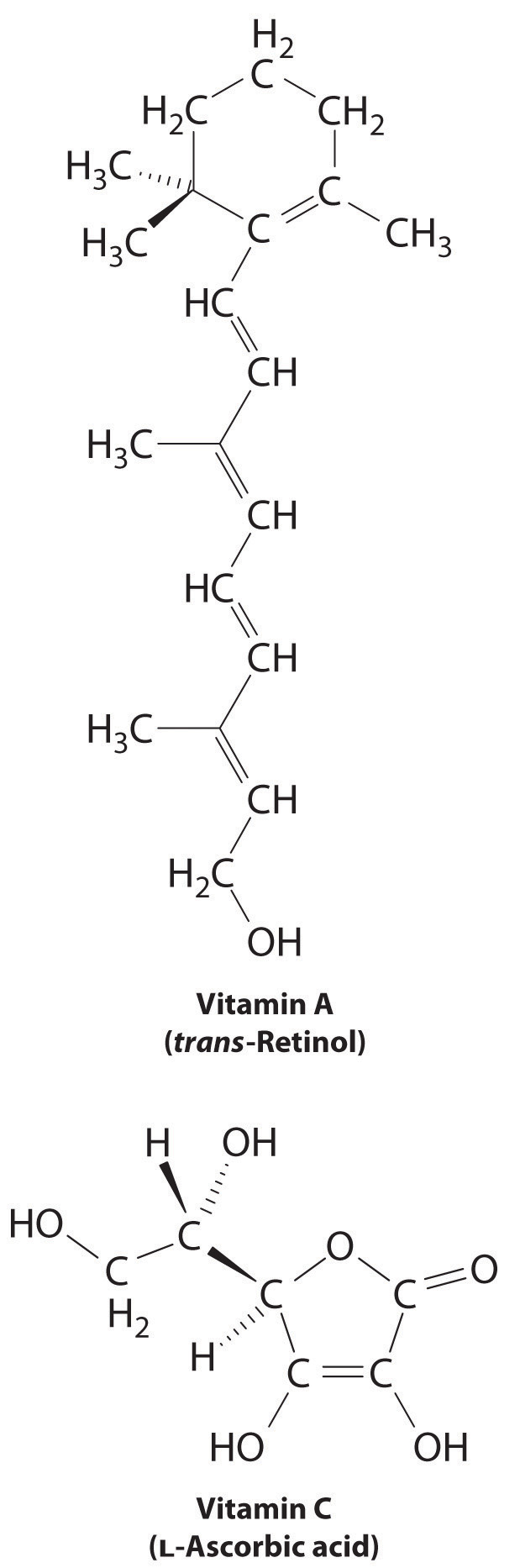
Because water-soluble vitamins are rapidly excreted, the risk of consuming them in excess is relatively small. Eating a dozen oranges a day is likely to make you tired of oranges long before you suffer any ill effects due to their high vitamin C content. In contrast, fat-soluble vitamins constitute a significant health hazard when consumed in large amounts. For example, the livers of polar bears and other large animals that live in cold climates contain large amounts of vitamin A, which have occasionally proven fatal to humans who have eaten them.
The following substances are essential components of the human diet:
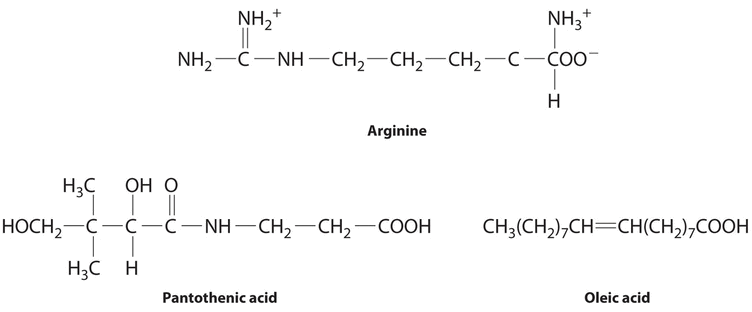
Using what you know of hydrophilic and hydrophobic solutes, classify each as water soluble or fat soluble and predict which are likely to be required in the diet on a daily basis.
- arginine
- pantothenic acid
- oleic acid
Given: chemical structures
Asked for: classification as water soluble or fat soluble; dietary requirement
Strategy:
Based on the structure of each compound, decide whether it is hydrophilic or hydrophobic. If it is hydrophilic, it is likely to be required on a daily basis.
Solution:
- Arginine is a highly polar molecule with two positively charged groups and one negatively charged group, all of which can form hydrogen bonds with water. As a result, it is hydrophilic and required in our daily diet.
- Although pantothenic acid contains a hydrophobic hydrocarbon portion, it also contains several polar functional groups (\(\ce{–OH}\) and \(\ce{–CO_2H}\)) that should interact strongly with water. It is therefore likely to be water soluble and required in the diet. (In fact, pantothenic acid is almost always a component of multiple-vitamin tablets.)
- Oleic acid is a hydrophobic molecule with a single polar group at one end. It should be fat soluble and not required daily.
These compounds are consumed by humans: caffeine, acetaminophen, and vitamin D. Identify each as primarily hydrophilic (water soluble) or hydrophobic (fat soluble), and predict whether each is likely to be excreted from the body rapidly or slowly.

- Answer
-
Caffeine and acetaminophen are water soluble and rapidly excreted, whereas vitamin D is fat soluble and slowly excreted
Solid Solutions
Solutions are not limited to gases and liquids; solid solutions also exist. For example, amalgams, which are usually solids, are solutions of metals in liquid mercury. Because most metals are soluble in mercury, amalgams are used in gold mining, dentistry, and many other applications. A major difficulty when mining gold is separating very small particles of pure gold from tons of crushed rock. One way to accomplish this is to agitate a suspension of the crushed rock with liquid mercury, which dissolves the gold (as well as any metallic silver that might be present). The very dense liquid gold–mercury amalgam is then isolated and the mercury distilled away.
An alloy is a solid or liquid solution that consists of one or more elements in a metallic matrix. A solid alloy has a single homogeneous phase in which the crystal structure of the solvent remains unchanged by the presence of the solute. Thus the microstructure of the alloy is uniform throughout the sample. Examples are substitutional and interstitial alloys such as brass or solder. Liquid alloys include sodium/potassium and gold/mercury. In contrast, a partial alloy solution has two or more phases that can be homogeneous in the distribution of the components, but the microstructures of the two phases are not the same. As a liquid solution of lead and tin is cooled, for example, different crystalline phases form at different cooling temperatures. Alloys usually have properties that differ from those of the component elements.
Network solids such as diamond, graphite, and \(\ce{SiO_2}\) are insoluble in all solvents with which they do not react chemically. The covalent bonds that hold the network or lattice together are simply too strong to be broken under normal conditions. They are certainly much stronger than any conceivable combination of intermolecular interactions that might occur in solution. Most metals are insoluble in virtually all solvents for the same reason: the delocalized metallic bonding is much stronger than any favorable metal atom–solvent interactions. Many metals react with solutions such as aqueous acids or bases to produce a solution. However, as we saw in Section 13.1, in these instances the metal undergoes a chemical transformation that cannot be reversed by simply removing the solvent.
Solids with very strong intermolecular bonding tend to be insoluble.
Solubilities of Ionic Substances in Liquids
Previously, you were introduced to guidelines for predicting the solubility of ionic compounds in water. Ionic substances are generally most soluble in polar solvents; the higher the lattice energy, the more polar the solvent must be to overcome the lattice energy and dissolve the substance. Because of its high polarity, water is the most common solvent for ionic compounds. Many ionic compounds are soluble in other polar solvents, however, such as liquid ammonia, liquid hydrogen fluoride, and methanol. Because all these solvents consist of molecules that have relatively large dipole moments, they can interact favorably with the dissolved ions.
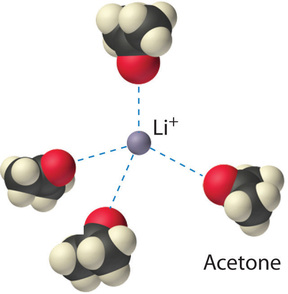
The ion–dipole interactions between \(\ce{Li^{+}}\) ions and acetone molecules in a solution of LiCl in acetone are shown in Figure \(\PageIndex{3}\). The energetically favorable \(\ce{Li^{+}}\)–acetone interactions make \(ΔH_3\) sufficiently negative to overcome the positive \(ΔH_1\) and \(ΔH_2\). Because the dipole moment of acetone (2.88 D), and thus its polarity, is actually larger than that of water (1.85 D), one might even expect that LiCl would be more soluble in acetone than in water. In fact, the opposite is true: 83 g of LiCl dissolve in 100 mL of water at 20°C, but only about 4.1 g of \(\ce{LiCl}\) dissolve in 100 mL of acetone. This apparent contradiction arises from the fact that the dipole moment is a property of a single molecule in the gas phase. A more useful measure of the ability of a solvent to dissolve ionic compounds is its dielectric constant (ε), which is the ability of a bulk substance to decrease the electrostatic forces between two charged particles. By definition, the dielectric constant of a vacuum is 1. In essence, a solvent with a high dielectric constant causes the charged particles to behave as if they have been moved farther apart. At 25°C, the dielectric constant of water is 80.1, one of the highest known, and that of acetone is only 21.0. Hence water is better able to decrease the electrostatic attraction between \(\ce{Li^{+}}\) and \(\ce{Cl^{-}}\) ions, so \(\ce{LiCl}\) is more soluble in water than in acetone. This behavior is in contrast to that of molecular substances, for which polarity is the dominant factor governing solubility.
A solvent’s dielectric constant is the most useful measure of its ability to dissolve ionic compounds. A solvent’s polarity is the dominant factor in dissolving molecular substances.
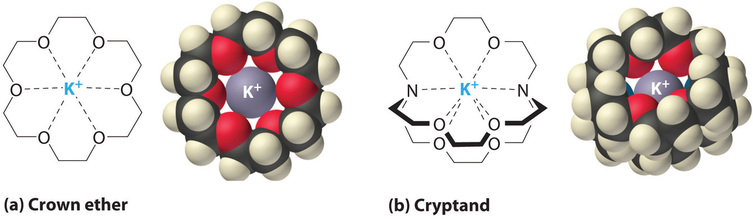
It is also possible to dissolve ionic compounds in organic solvents using crown ethers, cyclic compounds with the general formula \((OCH_2CH_2)_n\). Crown ethers are named using both the total number of atoms in the ring and the number of oxygen atoms. Thus 18-crown-6 is an 18-membered ring with six oxygen atoms (Figure \(\PageIndex{1a}\)). The cavity in the center of the crown ether molecule is lined with oxygen atoms and is large enough to be occupied by a cation, such as \(K^+\). The cation is stabilized by interacting with lone pairs of electrons on the surrounding oxygen atoms. Thus crown ethers solvate cations inside a hydrophilic cavity, whereas the outer shell, consisting of C–H bonds, is hydrophobic. Crown ethers are useful for dissolving ionic substances such as \(KMnO_4\) in organic solvents such as isopropanol \([(CH_3)_2CHOH]\) (Figure \(\PageIndex{5}\)). The availability of crown ethers with cavities of different sizes allows specific cations to be solvated with a high degree of selectivity.

Cryptands (from the Greek kryptós, meaning “hidden”) are compounds that can completely surround a cation with lone pairs of electrons on oxygen and nitrogen atoms (Figure \(\PageIndex{4b}\)). The number in the name of the cryptand is the number of oxygen atoms in each strand of the molecule. Like crown ethers, cryptands can be used to prepare solutions of ionic compounds in solvents that are otherwise too nonpolar to dissolve them.
Summary
The solubility of a substance is the maximum amount of a solute that can dissolve in a given quantity of solvent; it depends on the chemical nature of both the solute and the solvent and on the temperature and pressure. When a solution contains the maximum amount of solute that can dissolve under a given set of conditions, it is a saturated solution. Otherwise, it is unsaturated. Supersaturated solutions, which contain more dissolved solute than allowed under particular conditions, are not stable; the addition of a seed crystal, a small particle of solute, will usually cause the excess solute to crystallize. A system in which crystallization and dissolution occur at the same rate is in dynamic equilibrium. The solubility of a substance in a liquid is determined by intermolecular interactions, which also determine whether two liquids are miscible. Solutes can be classified as hydrophilic (water loving) or hydrophobic (water fearing). Vitamins with hydrophilic structures are water soluble, whereas those with hydrophobic structures are fat soluble. Many metals dissolve in liquid mercury to form amalgams. Covalent network solids and most metals are insoluble in nearly all solvents. The solubility of ionic compounds is largely determined by the dielectric constant (ε) of the solvent, a measure of its ability to decrease the electrostatic forces between charged particles. Solutions of many ionic compounds in organic solvents can be dissolved using crown ethers, cyclic polyethers large enough to accommodate a metal ion in the center, or cryptands, compounds that completely surround a cation.

