HW Solutions #8

UC Davis
Chemistry 2C

Unit 1: Electrochemistry  ●  Unit 2: Coordination Chemistry  ●  Unit 3: Descriptive Chemistry  ●  Unit 4: Chemical Kinetics  ●  Unit 5: Nuclear Chemistry
  Agenda  ●  Textbook  ●  ADAPT  ●  Worksheets

1. In the following decomposition reaction,

2 N₂O₅ → 4 NO₂ + O₂

oxygen gas is produced at the average rate of 9.1 × 10^-4 mol · L^-1 · s^-1. Over the same period, what is the average rate of the following:

• the production of nitrogen dioxide
• the loss of nitrogen pentoxide

Rachel

2. Consider the following reaction:

N₂(g) + 3 H₂(g) → 2 NH₃(g)

If the rate of loss of hydrogen gas is 0.03 mol · L^-1· s^-1, what is the rate of production of ammonia?

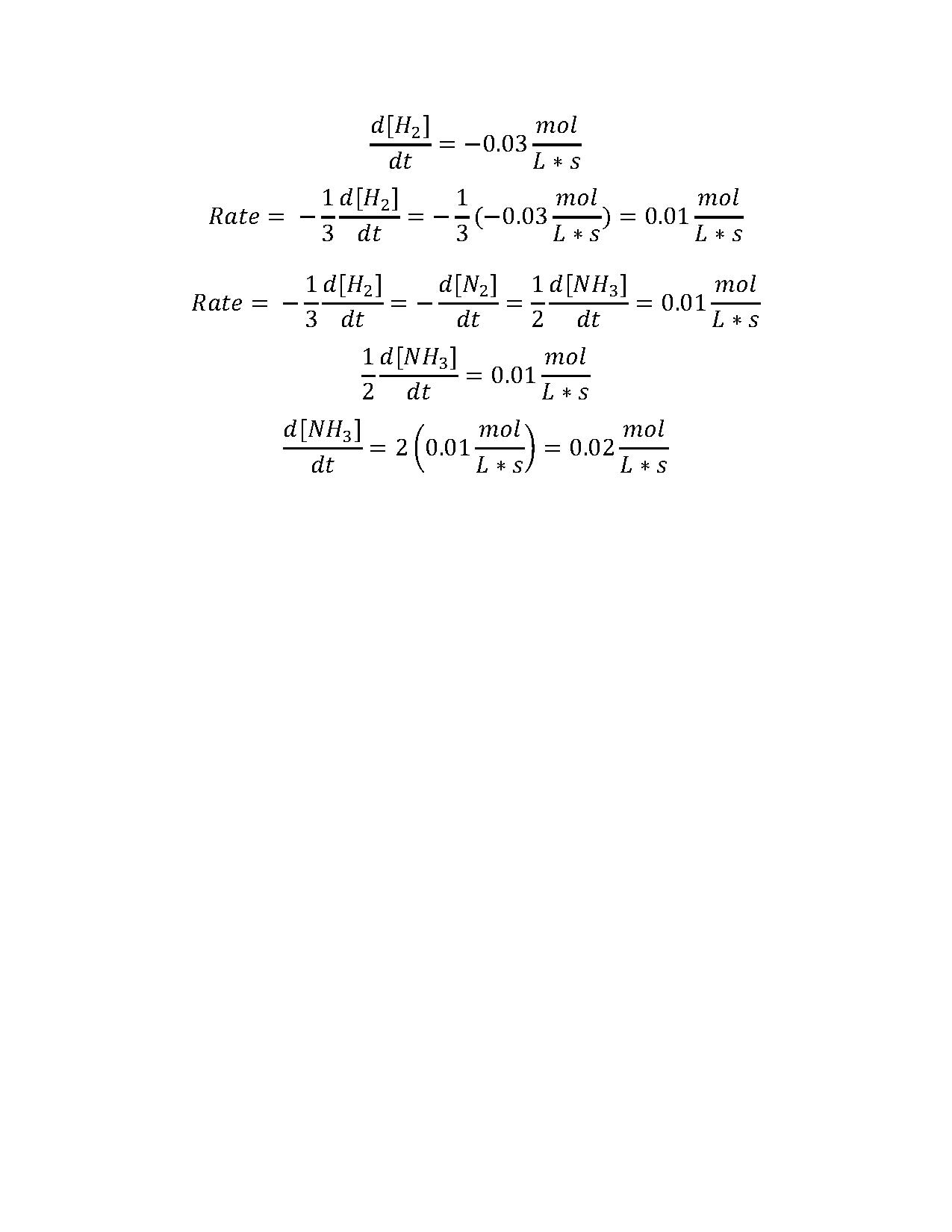
Rachel

3. Nitrogen monoxide reacts with hydrogen gas to produce nitrogen gas and water vapor. The mechanism is believed to be:

Step 1:	2 NO → N2O2
Step 2:	N2O2 + H2 → N2O + H2O
Step 3:	N2O + H2 → N2 + H2O

For this reaction find the following:

• the overall balanced equation
• 2NO + 2H₂ → N₂ + 2H₂0
• any reaction intermediates
• N₂O₂ and N₂O

4. Give two reasons why most molecular collisions do not lead to a reaction.

Generally, only a fraction of collision among gaseous molecules leads to a chemical reaction. In order for a reaction to occur molecules have to overcome an energy barrier called activation energy (minimum energy above the average kinetic that molecules must bring to their collisions in order for a reaction to occur). In other for this barrier to be overcome molecules most be accelerating at certain average kinetic energy. This can be influenced by increasing temperature, which accelerates the speed of the molecules thus leading to more collisions and a higher probability of a reaction occurring. An increase in temperature lowers the activation energy

Another important factor that could prevent molecular collisions leading to a reaction is the orientation of molecules at the time of collision

For a reaction to occur following a collision between molecules there must be a redistribution of energy that puts enough energy into certain key bonds to break them

5. An important function for managers is to determine the rate-determining steps in their business processes. In a certain fast-food restaurant, it takes 3 minutes to cook the food, 1.5 minutes to wrap the food, and 5 minutes to take the order and make change. How would a good manager assign the work to four employees?

The restaurant chain is a consecutive process. The processes are sequential and one cannot happen in isolation. The longest time which ( 5 minutes) is the time required to take the order and give change is the rate determining step of the business. In order to be effective the manager can assign two employees to the taking of the order and assigning change in order to reduce this time and possibly attend to other customers. While the other two employees can be assigned to cooking of the food and wrapping the food. During the down times or between orders, more people can always be shifted to the RDS.

6. For the hypothetical reaction

2A + 3B → 3C + 2D

the following rate data were obtained in three experiments at the same temperature:

Initial [A]	Initial [B]	Initial rate
(mole liter^-1)	(mole liter^-1')	(moles of A consumed liter^-1‘ sec^-1)
0.10	0.10	0.10
0.20	0.10	0.40
0.20	0.20	0.40

a.) Determine the experimental rate equation for the reaction

Rate Equation predicts the relationship between the rate of reaction and the concentration of the reaction in a chemical kinetics study.

Rate of Reaction=k[A]^m[B]ⁿ

Where [A] and [B] represents the reactant molarities and “m” and “n” are determined by the experiment and are not stoichiometric coefficients

To solve for “m” and “n”, first plug known values (rate, [A], and [B]) for each experiment:

Expt #1 (Rate₁): 0.10 =k[0.1]^m[0.1]ⁿ

Expt #2 (Rate₂): 0.40 =k[0.2]^m[0.1]ⁿ

Expt #3 (Rate₃): 0.40 =k[0.2]^m[0.2]ⁿ

Expt #1 and Expt #2 have equivalent [B] and thus, we can solve for “m” by dividing

Rate₁/Rate₂ = (0.1/0.4) = (k[0.1]^m[0.1]ⁿ)/(k[0.2]^m[0.1]ⁿ)

(0.1/0.4) = (0.1/0.2)^m

0.25=(0.5)^m

log(0.25)=mlog(0.5)

m=log(0.25)/log(0.5)

m=2

Expt #2 and Expt #3 have equivalent Rates (and [A]) and thus, we can solve for “n” by dividing

Rate₂/Rate₃ = (0.4/0.4) = (k[0.2]^m[0.1]ⁿ)/(k[0.2]^m[0.2]ⁿ)

1 = (0.1/0.2)ⁿ

1=(0.5)ⁿ

log(1)=nlog(0.5)

n=log(1)/log(0.5)

n=0

Plugging “m” and “n” to Rate of Reaction equation, Rate=k[A]^m[B]ⁿ gives:

Rate=k[A]²[B]⁰

Rate=k[A]²

b. Calculate the specific rate constant, k.

Rate = k[A]²

Plug in [A] and Rate from Expt#1 to solve for k: 0.40 = k [0.2]²

k=10

L s^-1moles^-2

(Note: Rates and [A] from Expt #2 and #3 should generate the same “k”)

c.) What is the rate of this reaction when [A] =0.30M and [B] = 0.30M?

Rate = k[A]²

Rate = (10)[0.30M]²

Rate = 0.90 L/s

_{Diana Wong}

7. For the hypothetical reaction

2A + B → 2C

the following data were collected in three experiments at 25°C:

Initial [A]	Initial [B]	Initial rate
(mole liter^-1)	(mole liter^-1)	(moles of A consumed liter^-1 sec^-1)
0.10	0.20	300
0.30	0.40	3600
0.30	0.80	14400

1. What is the experimental rate equation for this reaction?
   
   R=k[A]¹[B]²
   
   Solution:
   General equation: k[A]^m[B]ⁿ
   
   R₁= k[A]₁^m[B]₁ⁿ, R₂= k[A]₂^m[B]₂ⁿ, and R₃= k[A]₃^m[B]₃ⁿ , However we also know [A]₃=[A]₂ and [B]₃=2[B]₂
   
   Substitute this into R3 to give : R₃= k[A]₂^m(2[B]₂)ⁿ
   Divide the rates to find the increase: R₃/R₂ = 14400/3600 = 4
   Now Divide the equations for R₃ and R₂ the same way:
   
   R₃/R₂ = = (cancel like terms) = 2ⁿ
   We now have 2ⁿ = 4 and we can evaluate that n = 2 (2² = 4)
   
   Do the same with R₁ and R₂ to find m:
   R₁= 300 = k[A]₁^m[B]₁ⁿ = k(0.10)^m(0.20)² = k(0.10)^m0.04
   7500 = k(0.10)^m rearranging gives k= 7500/(0.1)^m
   
   R₂= 3600 = k[A]₂^m[B]₂ⁿ = k(0.30)^m(0.40)² = k(0.30)^m0.016
   22500 = k(0.30)^m rearranging gives k= 22500/(0.3)^m
   
   7500/(0.1)^m = 22500/(0.3)^m
   
   (0.3)^m/(0.1)^m = 22500/7500
   (0.3/0.1)^m = 3
   3^m = 3
   
   m = 1
   
   R=k[A]¹[B]<sup>2
   
   
   - John O.</sup>
   
   
   
2. Calculate the specific rate constant for this reaction.

300 = k(0.10)¹(0.20)² k = 75000

OR

3600 = k(0.30)¹(0.40)² k = 75000

OR

14400 = k(0.30)¹(0.80)² k = 75000

- John O.

8. In the reaction

2NO + Cl₂ → 2NOCl

the reactants and products are gases at the temperature of the reaction. The following rate data were measured for three experiments:

Initial p{NO}	Initial p{Cl2}	Initial rate
(atm)	(atm)	(moles of A consumed atm sec^-1)
0.50	0.50	5.1 x 10^-3
1.0	1.0	4.0 x 10^-2
0.50	1.0	1.0 x 10^-2

(a) From these data, write the rate equation for this gas reaction. What order is the reaction in NO, Cl₂, and overall?

If we double the initial pressure of NO, ceteris paribus, the rate is quadrupled. This means the reaction is second order for NO. If we double the pressure of Cl₂, ceteris paribus, the rate is approximated doubled as well, showing a first order reaction for Cl₂. The overall reaction has an order of the sum of the order of the reactants, 3. This is very similar to example 14-3 on page 579 of the text.

Sean Gottlieb

(b) Calculate the specific rate constant for this reaction.

Knowing the orders determined from part a) we can plug and chug to solve for k:

rate = k[NO]²[Cl₂]¹

5.1 x 10^-3 = k[0.5]²[0.5]

k = 0.0408 s^-1 atm^-2

This is similar to example 14-4 on page 580 of the text.

Sean Gottlieb

9. The reaction 2NO + O₂ → 2NO₂ is first order in oxygen pressure and second order in the pressure of nitric oxide. Write the rate expression.

Gaseous reactions are often measured in in terms of gas pressures

Rate = k * p{NO}² * p{O₂}¹

_{Diana Wong}

10. The reaction

A + B + C → D + F

was found to be zero order with respect to A. A solution of reactants A, B, and C was prepared with the following initial concentrations: 0.2M of A, 0.4M of B, and 0.6M of G. The concentration of A in this solution dropped to essentially zero in 5 min. A second solution was prepared with the following initial concentrations: 0.03M of A, 0.4M of B, and 0.6M of C. How long will it take for A to disappear?

11. For the reaction

2NO + H₂ → N₂O + H₂O

the following experimental rate data are collected in three successive experiments at the same temperature:

Initial [NO]	Initial [H2]	Initial rate
(mole liter^-1)	(mole liter^-1')	(moles of A consumed liter^-1‘ sec^-1)
0.60	0.37	0.18
1.20	0.37	0.72
1.20	0.74	1.44

Using these experimental data, write the rate expression for the reaction.

rate = k[NO]^m[H2]ⁿ

experiment 1: 0.18 molL^-1s^-1 = k(0.60 molL^-1)^m(0.37 molL^-1)ⁿ

experiment 2: 0.72 molL^-1s^-1 = k(1.20 molL^-1)^m(0.37 molL^-1)ⁿ

experiment 3: 1.44 molL^-1s^-1 = k(1.20 molL^-1)^m(0.74 molL^-1)ⁿ

equation 2 divided by 1: (0.72/0.18) = (1.20/0.60)^m m = 2

equation 3 divided by 2: (1.44/0.72) = (0.74/0.37)ⁿ n = 1

plug into equation 1: 0.18 molL^-1s^-1 = k(0.60 molL^-1)²(0.37 molL^-1)¹

solved k = 1.4 mol^-2L²s^-1

rate law: rate = 1.4 mol^-2L²s^-1[NO]²[H2]

---- Hao

12. The reaction

2HCrO₄^- + 3HSO₃^- + 5H⁺ → 2Cr³⁺ + 3SO₄^2- + 5HQO

follows the rate equation

Rate = k[HCrO₄^-][HSO₃^-]^₂[H⁺]

Why isn’t the rate proportional to the numbers of ions of each kind that are shown by the equation?

The rate has units molarity/time. So it is not dependent on just the number of moles, but the molarities of the reactants. Also, it is important to know that the order of the reaction for each reactant is not necessarily equal to its coefficient in the chemical equation.

Sean Gottlieb

13. The reaction SO₂Cl₂ —> SO₂ + Cl₂ is a first-order reaction with the rate constant k = 2.2 x 10^-5 sec^-1 at 320°C. What fraction of SO₂Cl₂ is decomposed on heating at 320°C for 90 min?

for first order reaction, ln([A]_o/[A]_t) = kt

for t = 90 min = 5400 s, ln([A]_o/[A]_t) = 2.2 X 10^-5 s^-1 X 5400 s

solved [A]_o/[A]_t = 1.13

fraction of decomposed SO₂Cl₂ = 1- [A]_t/[A]_o = 1-(1/1.13) = 0.11

---- Hao

14, It often is said that, near room temperature, a reaction rate doubles if the temperature is increased by 10°C. Calculate the activation energy of a reaction whose rate exactly doubles between 27°C and 37°C.

k=A exp[-Ea/(R*T)]

2k=A exp[-Ea/(R*(T+10))]

A exp[-Ea/(R*(T+10))]=2A exp[-Ea/(R*T)]

exp[-Ea/(R*(T+10))]=2*exp[-Ea/(R*T)]

-Ea/(R*(T+10))=ln(2) - Ea/(R*T)

-Ea/(R*(T+10)) + Ea/(R*T)=ln(2)

Ea/R [1/(T) + 1/(T+10)] = ln(2)

Ea = R*ln(2)/[1/300 - 1/310]= 54 kJ/mol

-Erik

15. What is the activation energy for a reaction for which an increase in temperature from 20°C to 30°C exactly triples the rate constant?

16. The following data give the temperature dependence of the rate constant for the reaction N₂O₄ → 2NO₂ → 1/2O₂. Plot the data and calculate the activation energy of the reaction.

T(K) k (sec^-1)
273 7.87 x 10^-7
298 3.46 x 10^-5
308 1.35 x 10^-4
318 4.98 x 10^-4
328 1.50 x 10^-3
338 4.87 x 10^-3

^{Plot ln(k) versus 1/T and construct a linear fit.}

From the arrhenius equation:

ln(k)=ln(A)-Ea/(RT)

Therefore: slope=-Ea/R

Ea=-slope*R=12376 (K) *8.314 (JK^-1mol^-1)= 102,894 J/mol ~ 103 kJ/mol

-Erik

17. Consider the reaction

CH₄ + Cl₂ → CH₃Cl + HCl (occurs under light)

The mechanism is a chain reaction involving Cl atoms and CH3 radicals. Which of the following steps does not terminate this chain reaction?

1. CH₃ + Cl → CH₃Cl
2. CH₃ + HCl → CH₄ + Cl
3. CH₃ + CH₃ → C₂H₂
4. Cl + Cl → Cl₂

Sean Gottlieb