6.E: Electronic Structure and Periodic Properties (Exercises)
- Last updated
- Save as PDF
- Page ID
- 77623
6.1: Electromagnetic Energy
Q6.1.1
The light produced by a red neon sign is due to the emission of light by excited neon atoms. Qualitatively describe the spectrum produced by passing light from a neon lamp through a prism.
S6.1.1
The spectrum consists of colored lines, at least one of which (probably the brightest) is red.
Q6.1.2
An FM radio station found at 103.1 on the FM dial broadcasts at a frequency of 1.031 × 108 s−1 (103.1 MHz). What is the wavelength of these radio waves in meters?
S6.1.2
\(λ=\dfrac{c}{ν}\)
\(λ = \dfrac{2.998 \times10^{8}\: \dfrac{m}{s}}{1.031 \times10^{8}\: \dfrac{1}{s}} = 2.908\:m\)
Q6.1.3
FM-95, an FM radio station, broadcasts at a frequency of 9.51 × 107 s−1 (95.1 MHz). What is the wavelength of these radio waves in meters?
S6.1.3
\(λ=\dfrac{c}{ν}\)
\(λ = \dfrac{2.998 \times10^{8}\: \dfrac{m}{s}}{9.51 \times10^{7}\: \dfrac{1}{s}} = 3.15 \:m\)
Q6.1.4
A bright violet line occurs at 435.8 nm in the emission spectrum of mercury vapor. What amount of energy, in joules, must be released by an electron in a mercury atom to produce a photon of this light?
S6.1.4
\(E= \dfrac{hc}{λ}\)
\(E= \dfrac{(2.998 \times 10^{8} \dfrac{m}{s})\: (6.6262 \times 10^{-34} Js)}{4.358 \times 10^{-7} m}\)
\(=4.56\times 10^{-19}J\)
Q6.1.5
Light with a wavelength of 614.5 nm looks orange. What is the energy, in joules, per photon of this orange light? What is the energy in eV (1 eV = 1.602 × 10−19 J)?
S6.1.5
1.) First convert 614.5 nm into meters
\(6.145 nm\) = \(6.145 \times10^{-7} m\)
2.) Then calculate the amount of energy this wavelength of light contains using the equations:
\(E = hν\) and \(ν=\dfrac{c}{λ}\) which can be manipulated algebraically into: \(E=\dfrac{hc}{λ}\)
- h = Plancks constant → \(6.6262 \times10^{-34} Js\)
- c = Speed of light → \(2.998\times 10^{8}\; \dfrac {m}{s}\)
- λ = wavelength of photon → \(6.145 \times10^{-7} m\)
\[= \dfrac{(6.6262\times 10^{−34}\;Js) \ (2.998\times 10^{8}\; \dfrac {m}{s}) } {6.145 \times 10^{−7}m \ } =3.233 \times 10^{-19} J\]
3.) Then convert Joules into eV:
\[=(3.233 \times 10^{−19}J) \times\dfrac{1eV}{1.602\times 10^{-19}J} \]\[=2.018 eV\]
Heated lithium atoms emit photons of light with an energy of 2.961 × 10−19 J. Calculate the frequency and wavelength of one of these photons. What is the total energy in 1 mole of these photons? What is the color of the emitted light?
S6.1.6
1.) \(E = hν\) and \(ν=\dfrac{E}{h}\)
- h = Plancks constant → \(6.6262 \times10^{-34} Js\)
Frequency: \(ν=\dfrac{ 2.961\times 10^{-19}J}{6.6262\times 10^{-34}Js}\ = 4.469\times 10^{14} Hz\)
2.) \(λ=\dfrac{c}{ν}\)
c = Speed of light → \(2.998\times 10^{8}\; \dfrac {m}{s}\)
Wavelength: \(λ=\dfrac{ 2.998\times 10^{8}\dfrac {m}{s}}{4.469\times 10^{14}\dfrac {1}{s}}\ = 6.709\times 10^{-7} m\) = Red Light
Total energy:
\(E= \dfrac{2.961 \times 10^{-19}J}{1\: photon}\times\dfrac{6.022\times 10^{23}\: photons}{1\: mole} = 1.783\times 10^{5} J \)
Q6.1.7
A photon of light produced by a surgical laser has an energy of 3.027 × 10−19 J. Calculate the frequency and wavelength of the photon. What is the total energy in 1 mole of photons? What is the color of the emitted light?
S6.1.7
ν = 4.568 × 1014 s; λ = 656.3 nm; Energy mol−1 = 1.823 × 105 J mol−1; red
Q6.1.8
When rubidium ions are heated to a high temperature, two lines are observed in its line spectrum at wavelengths (a) 7.9 × 10−7 m and (b) 4.2 × 10−7 m. What are the frequencies of the two lines? What color do we see when we heat a rubidium compound?
Q6.1.9
The emission spectrum of cesium contains two lines whose frequencies are (a) 3.45 × 1014 Hz and (b) 6.53 × 1014 Hz. What are the wavelengths and energies per photon of the two lines? What color are the lines?
S6.1.9
(a) λ = 8.69 × 10−7 m; E = 2.29 × 10−19 J; (b) λ = 4.59 × 10−7 m; E = 4.33 × 10−19 J; The color of (a) is red; (b) is blue.
Q6.1.10
Photons of infrared radiation are responsible for much of the warmth we feel when holding our hands before a fire. These photons will also warm other objects. How many infrared photons with a wavelength of 1.5 × 10−6 m must be absorbed by the water to warm a cup of water (175 g) from 25.0 °C to 40 °
S6.1.10
1.) First we must use the equation: q=mCΔT° to calculate the amount of Energy in Joules (J) to warm 175g of H2O a total of 15° Celsius
- m = mass in grams(g) → 175g
- C = Specific heat of H2O(l) → \(\dfrac {4.184 J}{g°C}\)
- ΔT° = Difference in temperature → 40 - 25 =15°
\[q = 175g\times \dfrac {4.184 J}{g°C}\times 15° C\]
q= 11,000 J
2.) Now we need to calculate the amount of energy in Joules (J) that one Photon with a wavelength of 1.5x10-6 m contains. We will use the equations:
\(E = hν\) and \(ν=\dfrac{c}{λ}\) which can be manipulated algebraically into: \(E=\dfrac{hc}{λ}\)
- h = Plancks constant → \(6.6262 \times10^{-34} Js\)
- c = Speed of light → \(2.998\times 10^{8}\; \dfrac {m}{s}\)
- λ = wavelength of photon → \(1.5 \times10^{-6} m\)
\[= \dfrac{(6.6262\times 10^{−34}\;Js) \ (2.998\times 10^{8}\; \dfrac {m}{s}) } {1.5 \times 10^{−6}m \ } =1.3 \times 10^{-19} J\]
This is the energy in one photon, so now we have to see how many times 1.3x10-19 J fits into the 11,000 J from our first calculation:
\[= \dfrac{11,000\;J} {1.3 \times 10^{−19}\; \dfrac {J}{photon} } =8.3\times 10^{22} photons\]
\[= 8.3\times 10^{22} photons\]
Q6.1.11
One of the radiographic devices used in a dentist's office emits an X-ray of wavelength 2.090 × 10−11 m. What is the energy, in joules, and frequency of this X-ray?
S6.1.11
E = 9.502 × 10−15 J; ν = 1.434 × 1019 s−1
Q6.1.12
The eyes of certain reptiles pass a single visual signal to the brain when the visual receptors are struck by photons of a wavelength of 850 nm. If a total energy of 3.15 × 10−14 J is required to trip the signal, what is the minimum number of photons that must strike the receptor?
S6.1.12
1.) First we need to convert nanometers to meters
850nm = 8.5 x 10-7 m
2. Then calculate Energy in Joules a photon of this wavelength (λ) produces:
\[(E=\dfrac{hc}{λ}) = \dfrac{(6.6262\times 10^{−34}\;Js) \ (2.998\times 10^{8}\; \dfrac {m}{s}) } {8.5 \times 10^{−7}m \ } = 2.3 \times 10^{-19} \dfrac {J}{photon}\]
3.) Then we need to find out how many of these photons it will take to trip the visual signal to the brain:
\[ \begin{align} &= \dfrac{3.15\times 10^{-14}\;\cancel{J}} {2.3 \times 10^{−19}\; \dfrac {\cancel{J}}{photon} } \\[5pt] &=1.3\times 10^{5}\, photons \end{align}\]
Q6.1.13
RGB color television and computer displays use cathode ray tubes that produce colors by mixing red, green, and blue light. If we look at the screen with a magnifying glass, we can see individual dots turn on and off as the colors change. Using a spectrum of visible light, determine the approximate wavelength of each of these colors. What is the frequency and energy of a photon of each of these colors?
S6.1.13
- Red: 660 nm; 4.54 × 1014 Hz; 3.01 × 10−19 J.
- Green: 520 nm; 5.77 × 1014 Hz; 3.82 × 10−19 J.
- Blue: 440 nm; 6.81 × 1014 Hz; 4.51 × 10−19 J.
Somewhat different numbers are also possible.
Q6.1.14
Answer the following questions about a Blu-ray laser:
- The laser on a Blu-ray player has a wavelength of 405 nm. In what region of the electromagnetic spectrum is this radiation? What is its frequency?
- A Blu-ray laser has a power of 5 milliwatts (1 watt = 1 J s−1). How many photons of light are produced by the laser in 1 hour?
- The ideal resolution of a player using a laser (such as a Blu-ray player), which determines how close together data can be stored on a compact disk, is determined using the following formula: Resolution = 0.60(λ/NA), where λ is the wavelength of the laser and NA is the numerical aperture. Numerical aperture is a measure of the size of the spot of light on the disk; the larger the NA, the smaller the spot. In a typical Blu-ray system, NA = 0.95. If the 405-nm laser is used in a Blu-ray player, what is the closest that information can be stored on a Blu-ray disk?
- The data density of a Blu-ray disk using a 405-nm laser is 1.5 × 107 bits mm−2. Disks have an outside diameter of 120 mm and a hole of 15-mm diameter. How many data bits can be contained on the disk? If a Blu-ray disk can hold 9,400,000 pages of text, how many data bits are needed for a typed page? (Hint: Determine the area of the disk that is available to hold data. The area inside a circle is given by A = πr2, where the radius r is one-half of the diameter.)
Q6.1.15
What is the threshold frequency for sodium metal if a photon with frequency 6.66 × 1014 s−1 ejects a photon with 7.74 × 10−20 J kinetic energy? Will the photoelectric effect be observed if sodium is exposed to orange light?
S6.1.15
5.49 × 1014 s−1; no
6.2: The Bohr Model
Q6.2.1
Why is the electron in a Bohr hydrogen atom bound less tightly when it has a quantum number of 3 than when it has a quantum number of 1?
Q6.2.2
What does it mean to say that the energy of the electrons in an atom is quantized?
S6.2.2
Quantized energy means that the electrons can possess only certain discrete energy values; values between those quantized values are not permitted.
Q6.2.3
Using the Bohr model, determine the energy, in joules, necessary to ionize a ground-state hydrogen atom. Show your calculations.
Q6.2.4
The electron volt (eV) is a convenient unit of energy for expressing atomic-scale energies. It is the amount of energy that an electron gains when subjected to a potential of 1 volt; \(1 \;eV = 1.602 \times 10^{-19}\; J\). Using the Bohr model, determine the energy, in electron volts, of the photon produced when an electron in a hydrogen atom moves from the orbit with \(n = 5\) to the orbit with \(n = 2\). Show your calculations.
S6.2.4
\[E=E_2−E_5=2.179 \times 10^{−18} \left (\dfrac{1}{n_2^2}−\dfrac{1}{n^2_5}\right) \; J\]
\[ = 2.179 \times 10^{-18} \left (\dfrac{1}{2^2}−\dfrac{1}{5^2}\right)=4.576 \times 10^{−19}\; J\]
\[= \dfrac{4.576\times 10^{−19}\;J} {1.602 \times 10^{−19}\;J \; eV^{−1} } =2.856\; eV\]
Q6.2.5
Using the Bohr model, determine the lowest possible energy for the electron in the \(He^+\) ion.
Q6.2.6
Using the Bohr model, determine the energy of an electron with \(n = 6\) in a hydrogen atom.
S6.2.6
−8.716 × 10−18 J
Q6.2.7
Using the Bohr model, determine the energy of an electron with \(n = 8\) in a hydrogen atom.
Q6.2.8
How far from the nucleus in angstroms (1 angstrom = \(1 \times 10^{–10}\; \ce m\)) is the electron in a hydrogen atom if it has an energy of \(-8.72 \times 10^{-20}\; \ce J\)?
S6.2.8
\(−3.405 \times 10^{−20} J\)
Q6.2.9
What is the radius, in angstroms, of the orbital of an electron with n = 8 in a hydrogen atom?
Q6.2.10
Using the Bohr model, determine the energy in joules of the photon produced when an electron in a \(\ce{He^{+}}\) ion moves from the orbit with n = 5 to the orbit with n = 2.
Q6.2.11
Using the Bohr model, determine the energy in joules of the photon produced when an electron in a Li2+ ion moves from the orbit with n = 2 to the orbit with n = 1.
S6.2.11
1.471 × 10−17 J
Q6.2.12
Consider a large number of hydrogen atoms with electrons randomly distributed in the n = 1, 2, 3, and 4 orbits
- How many different wavelengths of light are emitted by these atoms as the electrons fall into lower-energy orbitals?
- Calculate the lowest and highest energies of light produced by the transitions described in part (a).
- Calculate the frequencies and wavelengths of the light produced by the transitions described in part (b).
Q6.2.13
How are the Bohr model and the Rutherford model of the atom similar? How are they different?
Q6.2.14
The spectra of hydrogen and of calcium are shown in[link]. What causes the lines in these spectra? Why are the colors of the lines different? Suggest a reason for the observation that the spectrum of calcium is more complicated than the spectrum of hydrogen
S6.2.14
Both involve a relatively heavy nucleus with electrons moving around it, although strictly speaking, the Bohr model works only for one-electron atoms or ions. According to classical mechanics, the Rutherford model predicts a miniature “solar system” with electrons moving about the nucleus in circular or elliptical orbits that are confined to planes. If the requirements of classical electromagnetic theory that electrons in such orbits would emit electromagnetic radiation are ignored, such atoms would be stable, having constant energy and angular momentum, but would not emit any visible light (contrary to observation). If classical electromagnetic theory is applied, then the Rutherford atom would emit electromagnetic radiation of continually increasing frequency (contrary to the observed discrete spectra), thereby losing energy until the atom collapsed in an absurdly short time (contrary to the observed long-term stability of atoms). The Bohr model retains the classical mechanics view of circular orbits confined to planes having constant energy and angular momentum, but restricts these to quantized values dependent on a single quantum number, n. The orbiting electron in Bohr’s model is assumed not to emit any electromagnetic radiation while moving about the nucleus in its stationary orbits, but the atom can emit or absorb electromagnetic radiation when the electron changes from one orbit to another. Because of the quantized orbits, such “quantum jumps” will produce discrete spectra, in agreement with observations.
6.3: Development of Quantum Theory
Q6.3.1
How are the Bohr model and the quantum mechanical model of the hydrogen atom similar? How are they different?
S6.3.1
Both models have a central positively charged nucleus with electrons moving about the nucleus in accordance with the Coulomb electrostatic potential. The Bohr model assumes that the electrons move in circular orbits that have quantized energies, angular momentum, and radii that are specified by a single quantum number, n = 1, 2, 3, …, but this quantization is an ad hoc assumption made by Bohr to incorporate quantization into an essentially classical mechanics description of the atom. Bohr also assumed that electrons orbiting the nucleus normally do not emit or absorb electromagnetic radiation, but do so when the electron switches to a different orbit. In the quantum mechanical model, the electrons do not move in precise orbits (such orbits violate the Heisenberg uncertainty principle) and, instead, a probabilistic interpretation of the electron’s position at any given instant is used, with a mathematical function ψ called a wavefunction that can be used to determine the electron’s spatial probability distribution. These wavefunctions, or orbitals, are three-dimensional stationary waves that can be specified by three quantum numbers that arise naturally from their underlying mathematics (no ad hoc assumptions required): the principal quantum number, n (the same one used by Bohr), which specifies shells such that orbitals having the same n all have the same energy and approximately the same spatial extent; the angular momentum quantum number l, which is a measure of the orbital’s angular momentum and corresponds to the orbitals’ general shapes, as well as specifying subshells such that orbitals having the same l (and n) all have the same energy; and the orientation quantum number m, which is a measure of the z component of the angular momentum and corresponds to the orientations of the orbitals. The Bohr model gives the same expression for the energy as the quantum mechanical expression and, hence, both properly account for hydrogen’s discrete spectrum (an example of getting the right answers for the wrong reasons, something that many chemistry students can sympathize with), but gives the wrong expression for the angular momentum (Bohr orbits necessarily all have non-zero angular momentum, but some quantum orbitals [s orbitals] can have zero angular momentum).
Q6.3.2
What are the allowed values for each of the four quantum numbers: n, l, ml, and ms?
Q6.3.3
Describe the properties of an electron associated with each of the following four quantum numbers: n, l, ml, and ms.
S6.3.3
n determines the general range for the value of energy and the probable distances that the electron can be from the nucleus. l determines the shape of the orbital. ml determines the orientation of the orbitals of the same l value with respect to one another. ms determines the spin of an electron.
Q6.3.4
Answer the following questions:
- Without using quantum numbers, describe the differences between the shells, subshells, and orbitals of an atom.
- How do the quantum numbers of the shells, subshells, and orbitals of an atom differ?
Q6.3.5
Identify the subshell in which electrons with the following quantum numbers are found:
- n = 2, l = 1
- n = 4, l = 2
- n = 6, l = 0
S6.3.5
(a) 2p; (b) 4d; (c) 6s
Q6.3.6
Which of the subshells described in Question 5 contain degenerate orbitals? How many degenerate orbitals are in each?
Q6.3.7
Identify the subshell in which electrons with the following quantum numbers are found:
- n = 3, l = 2
- n = 1, l = 0
- n = 4, l = 3
S6.3.7
(a) 3d; (b) 1s; (c) 4f
Q6.3.8
Which of the subshells described in Question 7 contain degenerate orbitals? How many degenerate orbitals are in each?
Q6.3.9
Sketch the boundary surface of a \(d_{x^2−y^2}\) and a py orbital. Be sure to show and label the axes.
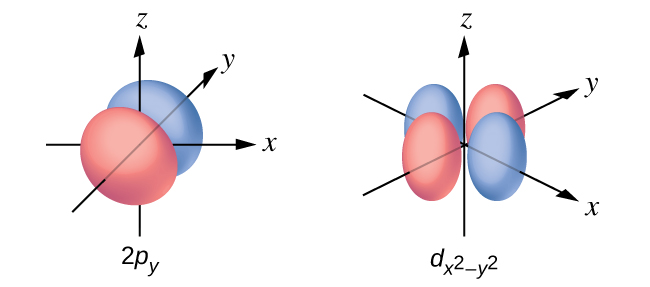
Q6.3.10
Sketch the px and dxz orbitals. Be sure to show and label the coordinates.
Q6.3.11
Consider the orbitals shown here in outline.
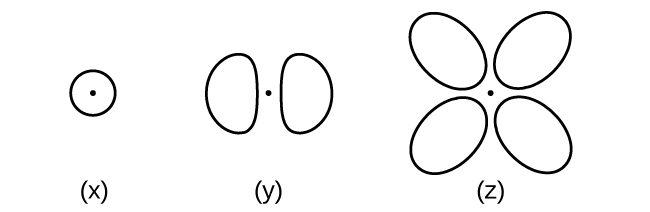
- What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?
- How many orbitals of type (x) are found in a shell with n = 2? How many of type (y)? How many of type (z)?
- Write a set of quantum numbers for an electron in an orbital of type (x) in a shell with n = 4. Of an orbital of type (y) in a shell with n = 2. Of an orbital of type (z) in a shell with n = 3.
- What is the smallest possible n value for an orbital of type (x)? Of type (y)? Of type (z)?
- What are the possible l and ml values for an orbital of type (x)? Of type (y)? Of type (z)?
S6.3.11
(a) x. 2, y. 2, z. 2; (b) x. 1, y. 3, z. 0; (c) x. 4 0 0 \(\dfrac{1}{2}\), y. 2 1 0 \(\dfrac{1}{2}\), z. 3 2 0 \(\dfrac{1}{2}\); (d) x. 1, y. 2, z. 3; (e) x. l = 0, ml = 0, y. l = 1, ml = –1, 0, or +1, z. l = 2, ml = –2, –1, 0, +1, +2
Q6.3.12
State the Heisenberg uncertainty principle. Describe briefly what the principle implies.
Q6.3.13
How many electrons could be held in the second shell of an atom if the spin quantum number ms could have three values instead of just two? (Hint: Consider the Pauli exclusion principle.)
S6.3.13
12
Q6.3.14
Which of the following equations describe particle-like behavior? Which describe wavelike behavior? Do any involve both types of behavior? Describe the reasons for your choices.
- \(c = λν\)
- \(E=\dfrac{mν^2}{2}\)
- \(r=\dfrac{n^2a_0}{Z}\)
- \(E = hν\)
- \(λ=\dfrac{h}{mν}\)
Q6.3.15
Write a set of quantum numbers for each of the electrons with an n of 4 in a Se atom.
S6.3.15
| n | l | ml | s |
|---|---|---|---|
| 4 | 0 | 0 | \(+\dfrac{1}{2}\) |
| 4 | 0 | 0 | \(−\dfrac{1}{2}\) |
| 4 | 1 | −1 | \(+\dfrac{1}{2}\) |
| 4 | 1 | 0 | \(+\dfrac{1}{2}\) |
| 4 | 1 | +1 | \(+\dfrac{1}{2}\) |
| 4 | 1 | −1 | \(−\dfrac{1}{2}\) |
6.4: Electronic Structure of Atoms (Electron Configurations)
Q6.4.1
Read the labels of several commercial products and identify monatomic ions of at least four transition elements contained in the products. Write the complete electron configurations of these cations.
Q6.4.2
Read the labels of several commercial products and identify monatomic ions of at least six main group elements contained in the products. Write the complete electron configurations of these cations and anions.
S6.4.2
For example, Na+: 1s22s22p6; Ca2+: 1s22s22p6; Sn2+: 1s22s22p63s23p63d104s24p64d105s2; F–: 1s22s22p6; O2–: 1s22s22p6; Cl–: 1s22s22p63s23p6.
Q6.4.3
Using complete subshell notation (not abbreviations, 1s22s22p6, and so forth), predict the electron configuration of each of the following atoms:
- C
- P
- V
- Sb
- Sm
S6.4.3
a.) 1s22s22p2
b.) 1s22s22p63s23p3
c.) 1s22s22p63s23p63d34s2
d.) 1s22s22p63s23p63d104s24p64d105s25p3
e.) 1s22s22p63s23p63d104s24p64d104f65s25p66s2
Q6.4.4
Using complete subshell notation (1s22s22p6, and so forth), predict the electron configuration of each of the following atoms:
- N
- Si
- Fe
- Te
- Tb
S6.4.4
- 1s22s22p3;
- 1s22s22p63s23p2;
- 1s22s22p63s23p64s23d6;
- 1s22s22p63s23p64s23d104p65s24d105p4;
- 1s22s22p63s23p64s23d104p65s24d105p66s24f9
Q6.4.5
Is 1s22s22p6 the symbol for a macroscopic property or a microscopic property of an element? Explain your answer.
Q6.4.6
What additional information do we need to answer the question “Which ion has the electron configuration 1s22s22p63s23p6”?
S6.4.6
The charge on the ion.
Q6.4.7
Draw the orbital diagram for the valence shell of each of the following atoms:
- C
- P
- V
- Sb
- Ru
Q6.4.8
Use an orbital diagram to describe the electron configuration of the valence shell of each of the following atoms:
- N
- Si
- Fe
- Te
- Mo
S6.4.8
(a)





Q6.4.9
Using complete subshell notation (1s22s22p6, and so forth), predict the electron configurations of the following ions.
- N3–
- Ca2+
- S–
- Cs2+
- Cr2+
- Gd3+
Q6.4.10
Which atom has the electron configuration: 1s22s22p63s23p64s23d104p65s24d2?
S6.4.10
Zr
Q6.4.11
Which atom has the electron configuration: 1s22s22p63s23p63d74s2?
S6.4.11
Co ; Cobalt
Q6.4.12
Which ion with a +1 charge has the electron configuration 1s22s22p63s23p63d104s24p6? Which ion with a –2 charge has this configuration?
S6.4.12
Rb+, Se2−
Q6.4.13
Which of the following atoms contains only three valence electrons: Li, B, N, F, Ne?
S6.4.13
B ; Boron
Q6.4.14
Which of the following has two unpaired electrons?
- Mg
- Si
- S
- Both Mg and S
- Both Si and S.
S6.4.14
Although both (b) and (c) are correct, (e) encompasses both and is the best answer.
Q6.4.15
Which atom would be expected to have a half-filled 6p subshell?
S6.4.15
Bi ; Bismuth
Q6.4.16
Which atom would be expected to have a half-filled 4s subshell?
S6.4.16
K
Q6.4.17
In one area of Australia, the cattle did not thrive despite the presence of suitable forage. An investigation showed the cause to be the absence of sufficient cobalt in the soil. Cobalt forms cations in two oxidation states, Co2+ and Co3+. Write the electron structure of the two cations.
Q6.4.18
Thallium was used as a poison in the Agatha Christie mystery story “The Pale Horse.” Thallium has two possible cationic forms, +1 and +3. The +1 compounds are the more stable. Write the electron structure of the +1 cation of thallium.
S6.4.18
1s22s22p63s23p63d104s24p64d105s25p66s24f145d10
Q6.4.19
Write the electron configurations for the following atoms or ions:
- B3+
- O–
- Cl3+
- Ca2+
- Ti
Q6.4.20
Cobalt–60 and iodine–131 are radioactive isotopes commonly used in nuclear medicine. How many protons, neutrons, and electrons are in atoms of these isotopes? Write the complete electron configuration for each isotope.
S6.4.20
Co has 27 protons, 27 electrons, and 33 neutrons: 1s22s22p63s23p64s23d7.
I has 53 protons, 53 electrons, and 78 neutrons: 1s22s22p63s23p63d104s24p64d105s25p5.
Q6.4.21
Write a set of quantum numbers for each of the electrons with an n of 3 in a Sc atom.
6.5: Periodic Variations in Element Properties
Q6.5.1
Based on their positions in the periodic table, predict which has the smallest atomic radius: Mg, Sr, Si, Cl, I.
S6.5.1
Cl
Q6.5.2
Based on their positions in the periodic table, predict which has the largest atomic radius: Li, Rb, N, F, I.
Q6.5.3
Based on their positions in the periodic table, predict which has the largest first ionization energy: Mg, Ba, B, O, Te.
S6.5.3
O
Q6.5.4
Based on their positions in the periodic table, predict which has the smallest first ionization energy: Li, Cs, N, F, I.
Q6.5.5
Based on their positions in the periodic table, rank the following atoms in order of increasing first ionization energy: F, Li, N, Rb
S6.5.5
Rb < Li < N < F
Q6.5.6
Based on their positions in the periodic table, rank the following atoms or compounds in order of increasing first ionization energy: Mg, O, S, Si
Q6.5.7
Atoms of which group in the periodic table have a valence shell electron configuration of ns2np3?
S6.5.7
15 (5A)
Q6.5.8
Atoms of which group in the periodic table have a valence shell electron configuration of ns2?
Q6.5.9
Based on their positions in the periodic table, list the following atoms in order of increasing radius: Mg, Ca, Rb, Cs.
S6.5.9
Mg < Ca < Rb < Cs
Q6.5.10
Based on their positions in the periodic table, list the following atoms in order of increasing radius: Sr, Ca, Si, Cl.
Q6.5.11
Based on their positions in the periodic table, list the following ions in order of increasing radius: K+, Ca2+, Al3+, Si4+.
S6.5.11
Si4+ < Al3+ < Ca2+ < K+
Q6.5.12
List the following ions in order of increasing radius: Li+, Mg2+, Br–, Te2–.
Q6.5.13
Which atom and/or ion is (are) isoelectronic with Br+: Se2+, Se, As–, Kr, Ga3+, Cl–?
S6.5.13
Se, As−
Q6.5.14
Which of the following atoms and ions is (are) isoelectronic with S2+: Si4+, Cl3+, Ar, As3+, Si, Al3+?
Q6.5.15
Compare both the numbers of protons and electrons present in each to rank the following ions in order of increasing radius: As3–, Br–, K+, Mg2+.
S6.5.15
Mg2+ < K+ < Br– < As3–
Q6.5.16
Of the five elements Al, Cl, I, Na, Rb, which has the most exothermic reaction? (E represents an atom.) What name is given to the energy for the reaction? Hint: note the process depicted does not correspond to electron affinity
\(\ce{E+}(g)+\ce{e-}⟶\ce{E}(g)\)
Q6.5.17
Of the five elements Sn, Si, Sb, O, Te, which has the most endothermic reaction? (E represents an atom.) What name is given to the energy for the reaction?
\[\ce{E}(g)⟶\ce{E+}(g)+\ce{e-}\]
S6.5.17
O, IE1
Q6.5.18
The ionic radii of the ions S2–, Cl–, and K+ are 184, 181, 138 pm respectively. Explain why these ions have different sizes even though they contain the same number of electrons.
Q6.5.19
Which main group atom would be expected to have the lowest second ionization energy?
S6.5.19
Ra
Q6.5.20
Explain why Al is a member of group 13 rather than group 3?


