5.7: Periodic Properties of the Elements
- Page ID
- 3504
Make sure you thoroughly understand the following essential ideas:
- You should be able to sketch out the general form of the periodic table and identify the various blocks and identify the groups corresponding to the alkali metals, the transition elements, the halogens, and the noble gases.
- For the first eighteen elements, you should be able to predict the formulas of typical binary compounds they can be expected to form with hydrogen and with oxygen.
- Comment on the concept of the "size" of an atom, and give examples of how radii are defined in at least two classes of of substances.
- Define ionization energy and electron affinity, and explain the periodic general trends.
- State the meaning and significance of electronegativity.
The periodic table in the form originally published by Dmitri Mendeleev in 1869 was an attempt to list the chemical elements in order of their atomic weights, while breaking the list into rows in such a way that elements having similar physical and chemical properies would be placed in each column. At that time, nothing was known about atoms; the development of the table was entirely empirical. Our goal in this lesson is to help you understand how the shape and organization of the modern periodic table are direct consequences of the atomic electronic structure of the elements.
Organization of the Periodic Table
To understand how the periodic table is organized, imagine that we write down a long horizontal list of the elements in order of their increasing atomic number. It would begin this way:
H He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca...
Now if we look at the various physical and chemical properties of these elements, we would find that their values tend to increase or decrease with Z in a manner that reveals a repeating pattern— that is, a periodicity. For the elements listed above, these breaks can be indicated by the vertical bars shown here in color:
H He | Li Be B C N O F Ne | Na Mg Al Si P S Cl Ar | Ca ...
Periods: To construct the table, we place each sequence in a separate row, which we call a period. The rows are aligned in such a way that the elements in each vertical column possess certain similarities. Thus the first short-period elements H and He are chemically similar to the elements Li and Ne at the beginning and end of the second period. The first period is split in order to place H above Li and He above Ne.
The "block" nomenclature shown above refers to the sub-orbital type (quantum number l, or s-p-d-f classification) of the highest-energy orbitals that are occupied in a given element. For n=1 there is no p block, and the s block is split so that helium is placed in the same group as the other inert gases, which it resembles chemically. For the second period (n=2) there is a p block but no d block; in the usual "long form" of the periodic table it is customary to leave a gap between these two blocks in order to accommodate the d blocks that occur at n=3 and above. At n=6 we introduce an f block, but in order to hold the table to reasonable dimensions the f blocks are placed below the main body of the table.
Groups: Each column of the periodic table is known as a group. The elements belonging to a given group bear a strong similarity in their chemical behaviors.
In the past, two different systems of Roman numerals and letters were used to denote the various groups. North Americans added the letter B to denote the d-block groups and A for the others; this is the system shown in the table above. The the rest of the world used A for the d-block elements and B for the others. In 1985, a new international system was adopted in which the columns were simply labeled 1-18. Although this system has met sufficient resistance in North America to slow its incorporation into textbooks, it seems likely that the "one to eighteen" system will gradually take over.
Families. Chemists have long found it convenient to refer to the elements of different groups, and in some cases of spans of groups by the names indicated in the table shown below. The two of these that are most important for you to know are the noble gases and thetransition metals.
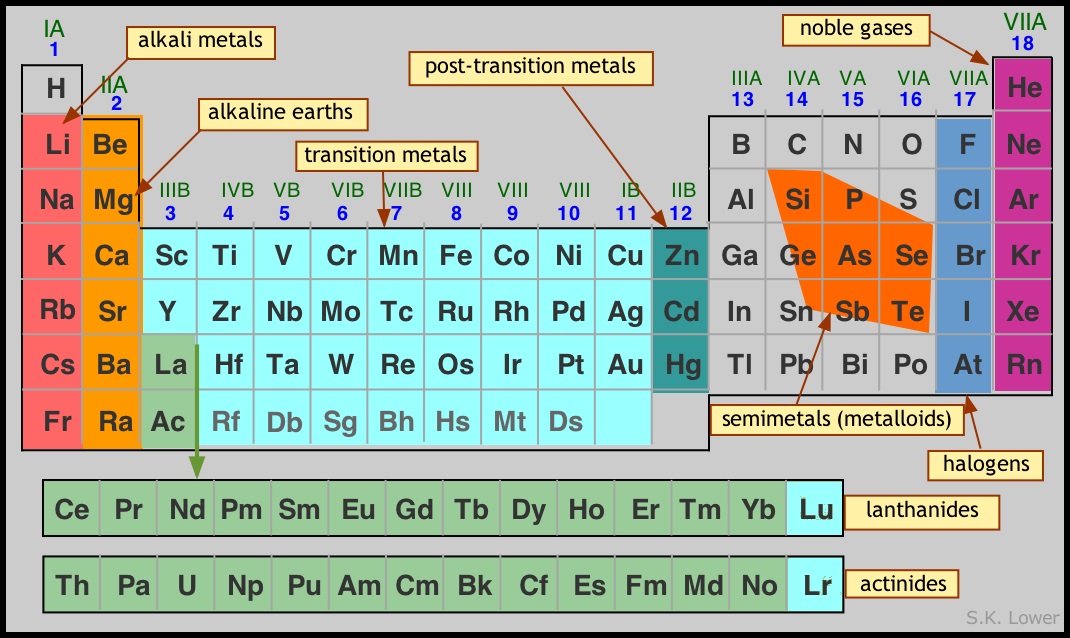
The shell model of the atom
The properties of an atom depend ultimately on the number of electrons in the various orbitals, and on the nuclear charge which determines the compactness of the orbitals. In order to relate the properties of the elements to their locations in the periodic table, it is often convenient to make use of a simplified view of the atom in which the nucleus is surrounded by one or more concentric spherical "shells", each of which consists of the highest-principal quantum number orbitals (always s- and p-orbitals) that contain at least one electron. The shell model (as with any scientific model) is less a description of the world than a simplified way of looking at it that helps us to understand and correlate diverse phenomena. The principal simplification here is that it deals only with the main group elements of the s- and p-blocks, omitting the d- and f-block elements whose properties tend to be less closely tied to their group numbers.
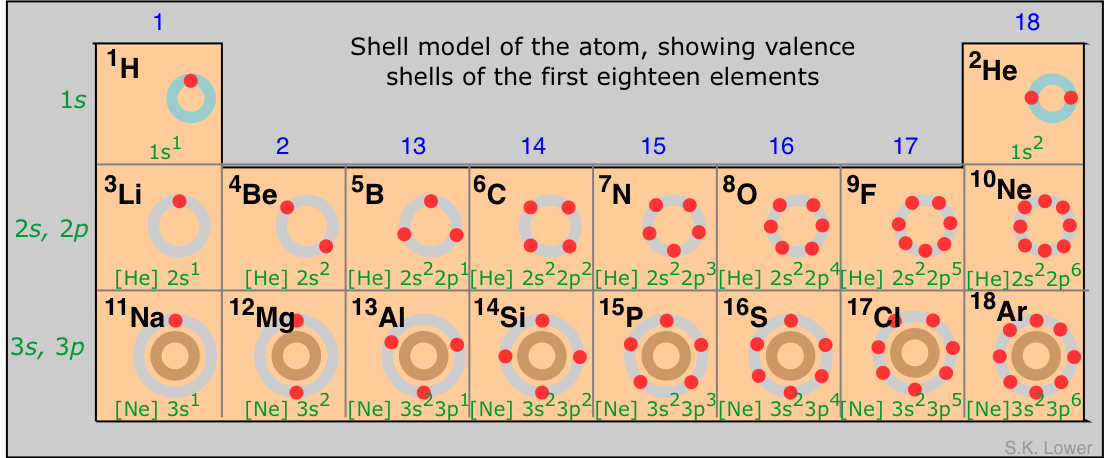
The electrons (denoted by the red dots) in the outer-most shell of an atom are the ones that interact most readily with other atoms, and thus play a major role in governing the chemistry of an element. Notice the use of noble-gas symbols to simplify the electron-configuration notation.
In particular, the number of outer-shell electrons (which is given by the rightmost digit in the group number) is a major determinant of an element's "combining power", or valence. The general trend is for an atom to gain or lose electrons, either directly (leading to formation of ions) or by sharing electrons with other atoms so as to achieve an outer-shell configuration of s2p6. This configuration, known as an octet, corresponds to that of one of the noble-gas elements of Group 18.
- the elements in Groups 1, 2 and 13 tend to give up their valence electrons to form positive ions such as Na+, Mg2+ and Al3+, as well as compounds NaH, MgH2 and AlH3. The outer-shell configurations of the metal atoms in these species correspond to that of neon.
- elements in Groups 15-17 tend to acquire electrons, forming ions such as P3–, S2– and Cl– or compounds such as PH3, H2S and HCl. The outer-shell configurations of these elements correspond to that of argon.
- the Group 14 elements do not normally form ions at all, but share electrons with other elements in tetravalent compounds such as CH4.
The above diagram shows the first three rows of what are known as the representative elements— that is, the s- and p-block elements only. As we move farther down (into the fourth row and below), the presence of d-electrons exerts a complicating influence which allows elements to exhibit multiple valances. This effect is especially noticeable in the transition-metal elements, and is the reason for not including the d-block with the representative elements at all.
Effective nuclear charge
Those electrons in the outmost or valence shell are especially important because they are the ones that can engage in the sharing and exchange that is responsible for chemical reactions; how tightly they are bound to the atom determines much of the chemistry of the element. The degree of binding is the result of two opposing forces: the attraction between the electron and the nucleus, and the repulsions between the electron in question and all the other electrons in the atom. All that matters is the net force, the difference between the nuclear attraction and the totality of the electron-electron repulsions.
We can simplify the shell model even further by imagining that the valence shell electrons are the only electrons in the atom, and that the nuclear charge has whatever value would be required to bind these electrons as tightly as is observed experimentally. Because the number of electrons in this model is less than the atomic number Z, the required nuclear charge will also be smaller. and is known as the effective nuclear charge. Effective nuclear charge is essentially the positive charge that a valence electron "sees".
Z vs. Zeffective
Part of the difference between Z and Zeffective is due to other electrons in the valence shell, but this is usually only a minor contributor because these electrons tend to act as if they are spread out in a diffuse spherical shell of larger radius. The main actors here are the electrons in the much more compact inner shells which surround the nucleus and exert what is often called a shielding or "screening" effect on the valence electrons.
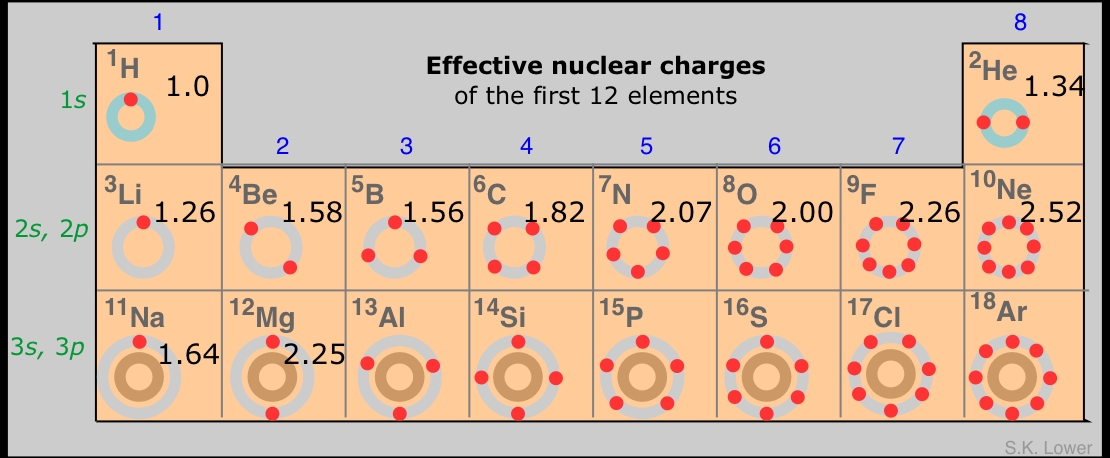
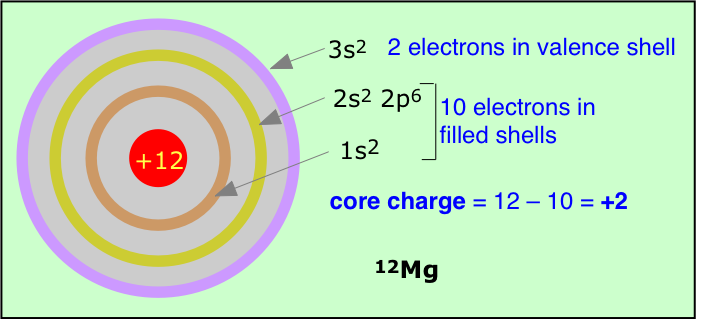
The formula for calculating effective nuclear charge is not very complicated, but we will skip a discussion of it here. An even simpler although rather crude procedure is to just subtract the number of inner-shell electrons from the nuclear charge; the result is a form of effective nuclear charge which is called the core charge of the atom.
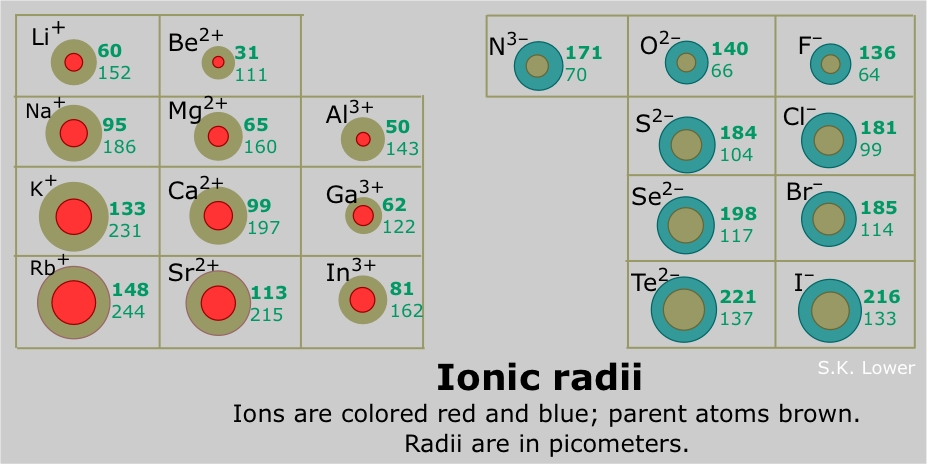
Sizes of atoms and ions
The concept of "size" is somewhat ambiguous when applied to the scale of atoms and molecules. The reason for this is apparent when you recall that an atom has no definite boundary; there is a finite (but very small) probability of finding the electron of a hydrogen atom, for example, 1 cm, or even 1 km from the nucleus. It is not possible to specify a definite value for the radius of an isolated atom; the best we can do is to define a spherical shell within whose radius some arbitrary percentage of the electron density can be found
.
When an atom is combined with other atoms in a solid element or compound, an effective radius can be determined by observing the distances between adjacent rows of atoms in these solids. This is most commonly carried out by X-ray scattering experiments. Because of the different ways in which atoms can aggregate together, several different kinds of atomic radii can be defined.
Note
Distances on the atomic scale have traditionally been expressed in Ångstrom units (1Å = 10–8 cm = 10–10 m), but nowadays the picometer is preferred:
1 pm = 10–12 m = 10–10 cm = 10–2 Å, or 1Å = 100 pm.
The radii of atoms and ions are typically in the range 70-400 pm.
A rough idea of the size of a metallic atom can be obtained simply by measuring the density of a sample of the metal. This tells us the number of atoms per unit volume of the solid. The atoms are assumed to be spheres of radius r in contact with each other, each of which sits in a cubic box of edge length 2r. The volume of each box is just the total volume of the solid divided by the number of atoms in that mass of the solid; the atomic radius is the cube root of r.
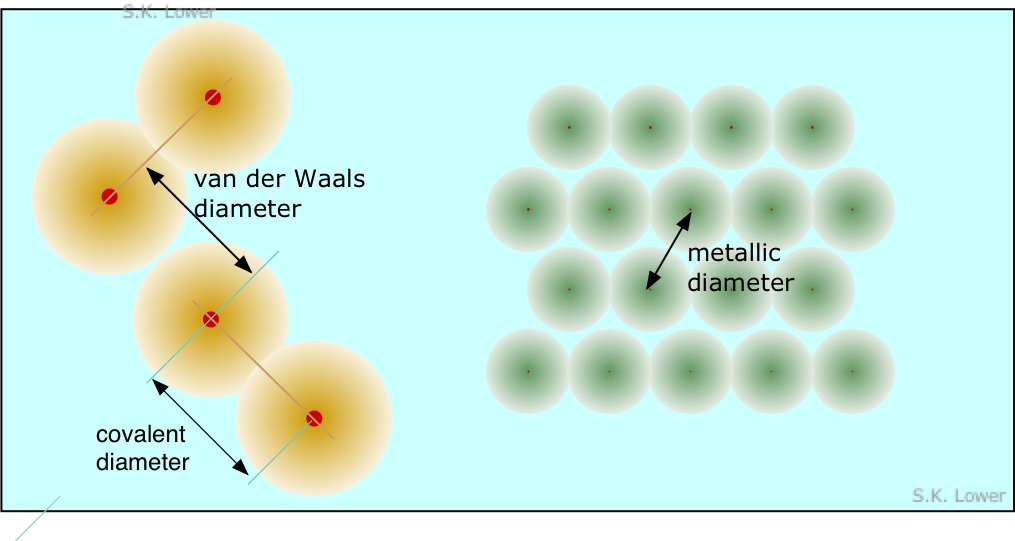
Although the radius of an atom or ion cannot be measured directly, in most cases it can be inferred from measurements of the distance between adjacent nuclei in a crystalline solid. This is most commonly carried out by X-ray scattering experiments. Because such solids fall into several different classes, several kinds of atomic radius are defined. Many atoms have several different radii; for example, sodium forms a metallic solid and thus has a metallic radius, it forms a gaseous molecule Na2 in the vapor phase (covalent radius), and of course it forms ionic solids such as NaCl.
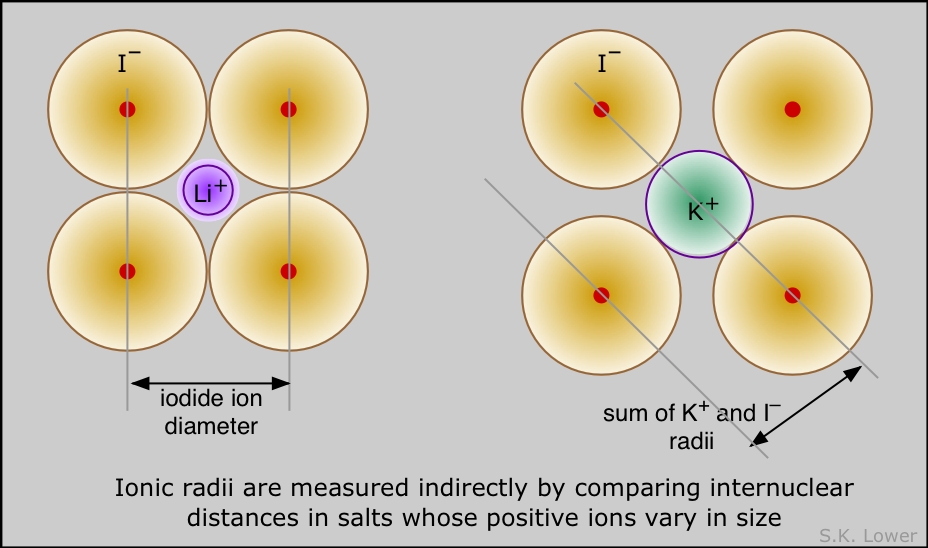
Ionic radius is the effective radius of ions in solids such as NaCl. It is easy enough to measure the distance between adjacent rows of Na+ and Cl– ions in such a crystal, but there is no unambiguous way to decide what portions of this distance are attributable to each ion. The best one can do is make estimates based on studies of several different ionic solids (LiI, KI, NaI, for example) that contain one ion in common. Many such estimates have been made, and they turn out to be remarkably consistent.
Many atoms have several different radii; for example, sodium forms a metallic solid and thus has a metallic radius, it forms a gaseous molecule Na2 in the vapor phase (covalent radius), and of course it forms ionic solids as mentioned above.
Periodic trends in atomic size
We would expect the size of an atom to depend mainly on the principal quantum number of the highest occupied orbital; in other words, on the "number of occupied electron shells". Since each row in the periodic table corresponds to an increment in n, atomic radius increases as we move down a column. The other important factor is the nuclear charge; the higher the atomic number, the more strongly will the electrons be drawn toward the nucleus, and the smaller the atom. This effect is responsible for the contraction we observe as we move across the periodic table from left to right.
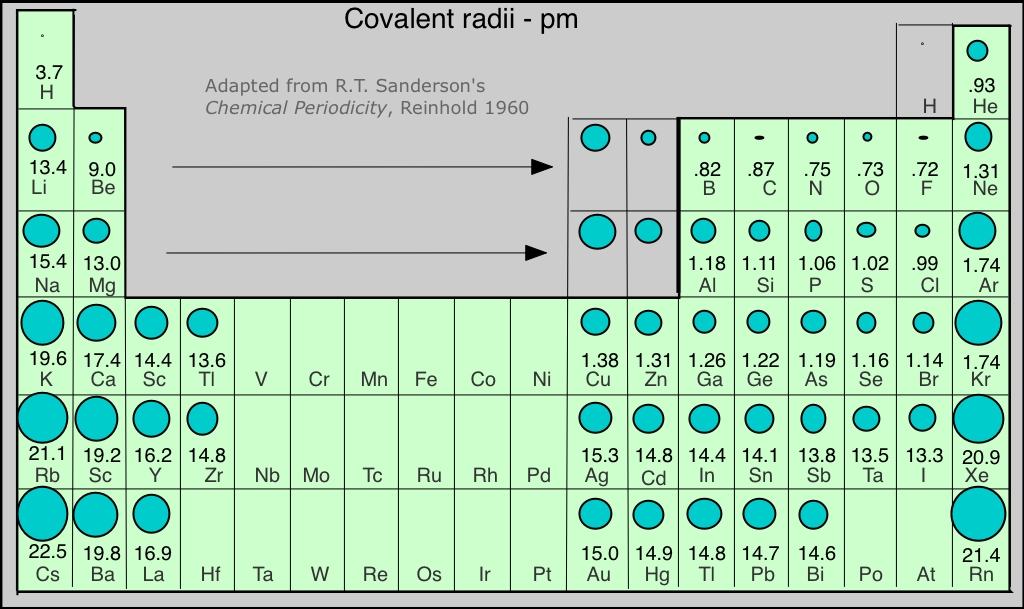
The figure shows a periodic table in which the sizes of the atoms are represented graphically. The apparent discontinuities in this diagram reflect the difficulty of comparing the radii of atoms of metallic and nonmetallic bonding types. Radii of the noble gas elements are estimates from those of nearby elements.
Ionic radii
A positive ion is always smaller than the neutral atom, owing to the diminished electron-electron repulsion. If a second electron is lost, the ion gets even smaller; for example, the ionic radius of Fe2+ is 76 pm, while that of Fe3+ is 65 pm. If formation of the ion involves complete emptying of the outer shell, then the decrease in radius is especially great.
The hydrogen ion H+ is in a class by itself; having no electron cloud at all, its radius is that of the bare proton, or about 0.1 pm— a contraction of 99.999%! Because the unit positive charge is concentrated into such a small volume of space, the charge density of the hydrogen ion is extremely high; it interacts very strongly with other matter, including water molecules, and in aqueous solution it exists only as the hydronium ion H3O+.
Negative ions are always larger than the parent ion; the addition of one or more electrons to an existing shell increases electron-electron repulsion which results in a general expansion of the atom.
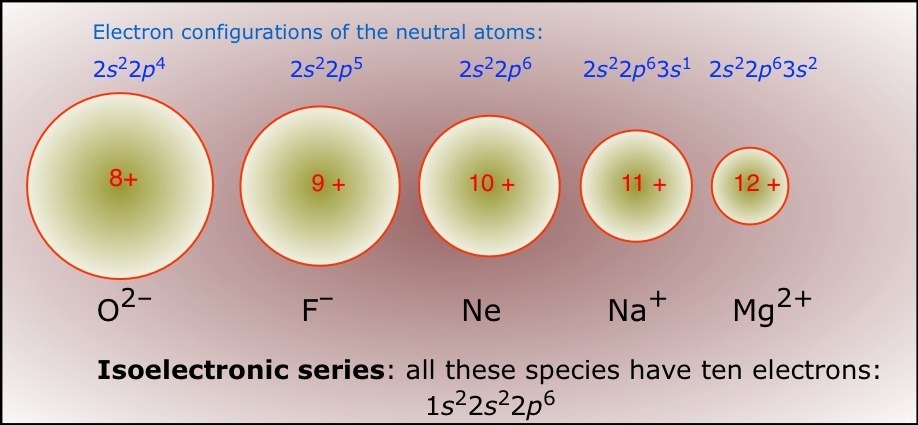
An isoelectronic series is a sequence of species all having the same number of electrons (and thus the same amount of electron-electron repulsion) but differing in nuclear charge. Of course, only one member of such a sequence can be a neutral atom (neon in the series shown below.) The effect of increasing nuclear charge on the radius is clearly seen.
Periodic Trends in ion formation
Chemical reactions are based largely on the interactions between the most loosely bound electrons in atoms, so it is not surprising that the tendency of an atom to gain, lose or share electrons is one of its fundamental chemical properties.
Ionization Energy
This term always refers to the formation of positive ions. In order to remove an electron from an atom, work must be done to overcome the electrostatic attraction between the electron and the nucleus; this work is called the ionization energy of the atom and corresponds to the exothermic process
\[M_{(g)} → M^+_{(g)} + e^–\]
where \(M_{(g)}\) stands for any isolated (gaseous) atom.
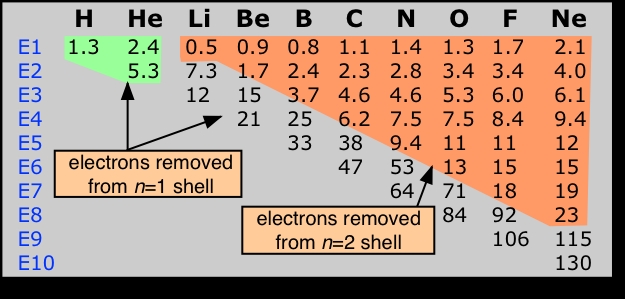
An atom has as many ionization energies as it has electrons. Electrons are always removed from the highest-energy occupied orbital. An examination of the successive ionization energies of the first ten elements (below) provides experimental confirmation that the binding of the two innermost electrons (1s orbital) is significantly different from that of the n=2 electrons.Successive ionization energies of an atom increase rapidly as reduced electron-electron repulsion causes the electron shells to contract, thus binding the electrons even more tightly to the nucleus.
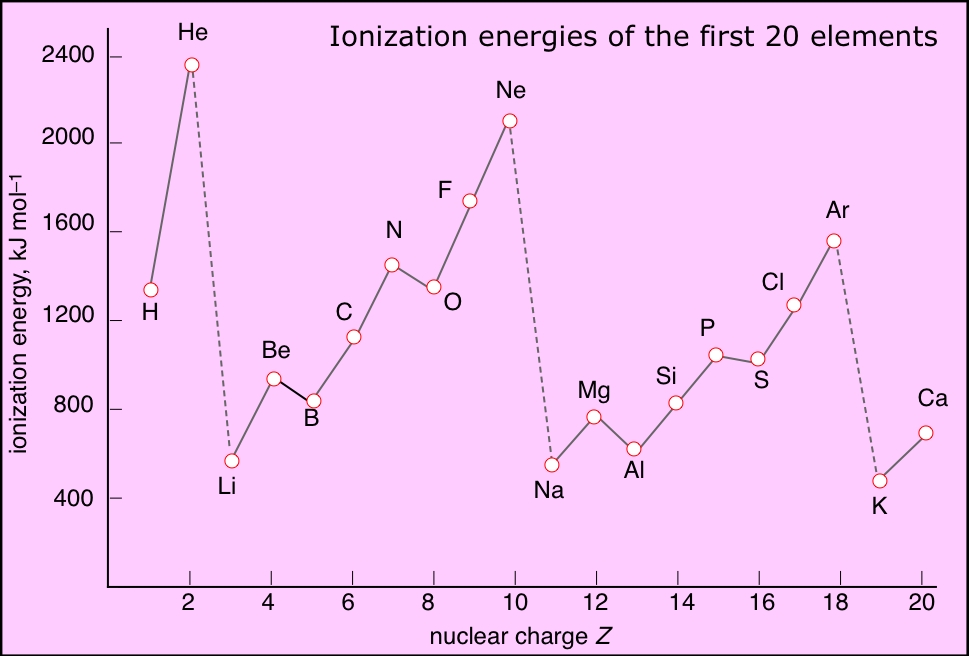
Ionization energies increase with the nuclear charge Z as we move across the periodic table. They decrease as we move down the table because in each period the electron is being removed from a shell one step farther from the nucleus than in the atom immediately above it. This results in the familiar zig-zag lines when the first ionization energies are plotted as a function of Z.
This more detailed plot of the ionization energies of the atoms of the first ten elements reveals some interesting irregularities that can be related to the slightly lower energies (greater stabilities) of electrons in half-filled (spin-unpaired) relative to completely-filled subshells.
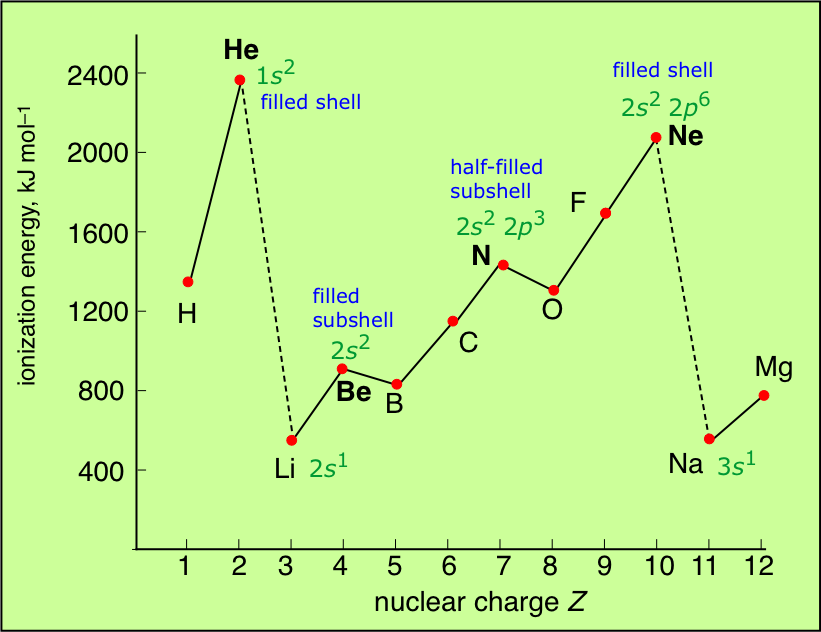
Finally, a more comprehensive survey of the ionization energies of the main group elements is shown below.
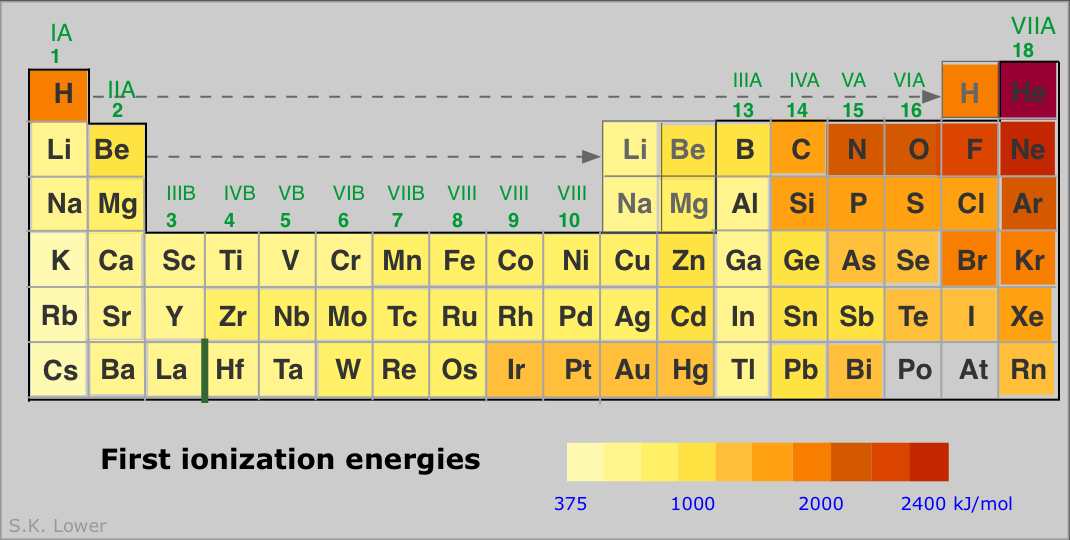
Some points to note:
- The noble gases have the highest IE's of any element in the period. This has nothing to do with any mysterious "special stability" of the s2p6 electron configuration; it is simply a matter of the high nuclear charge acting on more contracted orbitals.
- IE's (as well as many other properties) tend not to vary greatly amongst the d-block elements. This reflects the fact that as the more-compact d orbitals are being filled, they exert a screening effect that partly offsets that increasing nuclear charge on the outermost s orbitals of higher principal quantum number.
- Each of the Group 13 elements has a lower first-IE than that of the element preceding it. The reversal of the IE trend in this group is often attributed to the more easy removal of the single outer-shell p electron compared to that of electrons contained in filled (and thus spin-paired) s- and d-orbitals in the preceding elements.
Electron affinity
Formation of a negative ion occurs when an electron from some external source enters the atom and become incorporated into the lowest energy orbital that possesses a vacancy. Because the entering electron is attracted to the positive nucleus, the formation of negative ions is usually exothermic. The energy given off is the electron affinity of the atom. For some atoms, the electron affinity appears to be slightly negative, suggesting that electron-electron repulsion is the dominant factor in these instances.
In general, electron affinities tend to be much smaller than ionization energies, suggesting that they are controlled by opposing factors having similar magnitudes. These two factors are, as before, the nuclear charge and electron-electron repulsion. But the latter, only a minor actor in positive ion formation, is now much more significant. One reason for this is that the electrons contained in the inner shells of the atom exert a collective negative charge that partially cancels the charge of the nucleus, thus exerting a so-called shielding effect which diminishes the tendency for negative ions to form.
Because of these opposing effects, the periodic trends in electron affinities are not as clear as are those of ionization energies. This is particularly evident in the first few rows of the periodic table, in which small effects tend to be magnified anyway because an added electron produces a large percentage increase in the number of electrons in the atom.
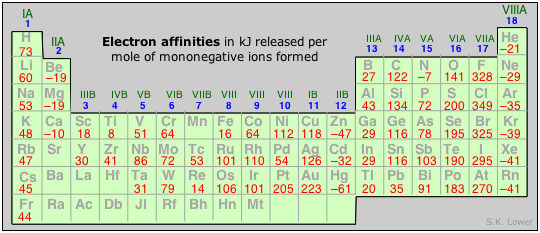
In general, we can say that electron affinities become more exothermic as we move from left to right across a period (owing to increased nuclear charge and smaller atom size). There are some interesting irregularities, however:
- In the Group 2 elements, the filled 2s orbital apparently shields the nucleus so effectively that the electron affinities are slightly endothermic.
- The Group 15 elements have rather low values, due possibly to the need to place the added electron in a half-filled p orbital; why the electron affinity of nitrogen should be endothermic is not clear. The vertical trend is for electron affinity to become less exothermic in successive periods owing to better shielding of the nucleus by more inner shells and the greater size of the atom, but here also there are some apparent anomalies.
Electronegativity
When two elements are joined in a chemical bond, the element that attracts the shared electrons more strongly is more electronegative. Elements with low electronegativities (the metallic elements) are said to be electropositive.
Electronegativities are properties of atoms that are chemically bound to each other; there is no way of measuring the electronegativity of an isolated atom.
Moreover, the same atom can exhibit different electronegativities in different chemical environments, so the "electronegativity of an element" is only a general guide to its chemical behavior rather than an exact specification of its behavior in a particular compound. Nevertheless, electronegativity is eminently useful in summarizing the chemical behavior of an element. You will make considerable use of electronegativity when you study chemical bonding and the chemistry of the individual elements.
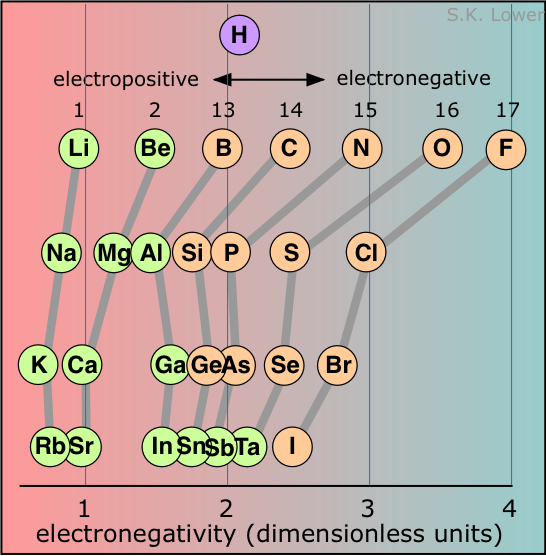
Because there is no single definition of electronegativity, any numerical scale for measuring it must of necessity be somewhat arbitrary. Most such scales are themselves based on atomic properties that are directly measurable and which relate in one way or the other to electron-attracting propensity. The most widely used of these scales was devised by Linus Pauling and is related to ionization energy and electron affinity. The Pauling scale runs from 0 to 4; the highest electron affinity, 4.0, is assigned to fluorine, while cesium has the lowest value of 0.7. Values less than about 2.2 are usually associated with electropositive, or metallic character. In the representation of the scale shown in figure, the elements are arranged in rows corresponding to their locations in the periodic table. The correlation is obvious; electronegativity is associated with the higher rows and the rightmost columns.
The location of hydrogen on this scale reflects some of the significant chemical properties of this element. Although it acts like a metallic element in many respects (forming a positive ion, for example), it can also form hydride-ion (H–) solids with the more electropositive elements, and of course its ability to share electrons with carbon and other p-block elements gives rise to a very rich chemistry, including of course the millions of organic compounds.


