4.18: Solutions to Selected Problems
- Page ID
- 194912
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 4.2.1:
a) 10 ppm b) 64 ppm c) 158 ppm
Exercise 4.2.2:
a) 63 ppm b) 201 ppm c) 71 ppm
Exercise 4.3.1:
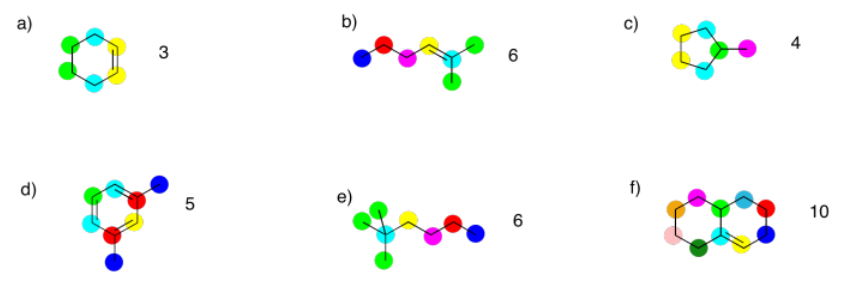
Exercise 4.3.2:
- pentane, CH3CH2CH2CH2CH3, or hexane, CH3CH2CH2CH2CH2CH3
- heptane, CH3CH2CH2CH2CH2CH2CH3, or octane, CH3CH2CH2CH2CH2CH2CH2CH3
- nonane, CH3CH2CH2CH2CH2CH2CH2CH2CH3, or decane, CH3CH2CH2CH2CH2CH2CH2CH2CH2CH3
Exercise 4.4.1:
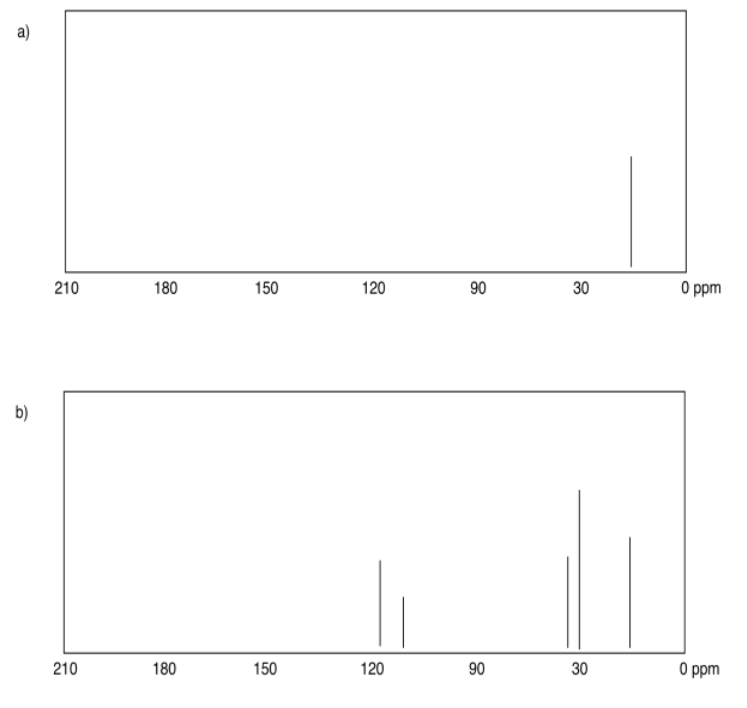
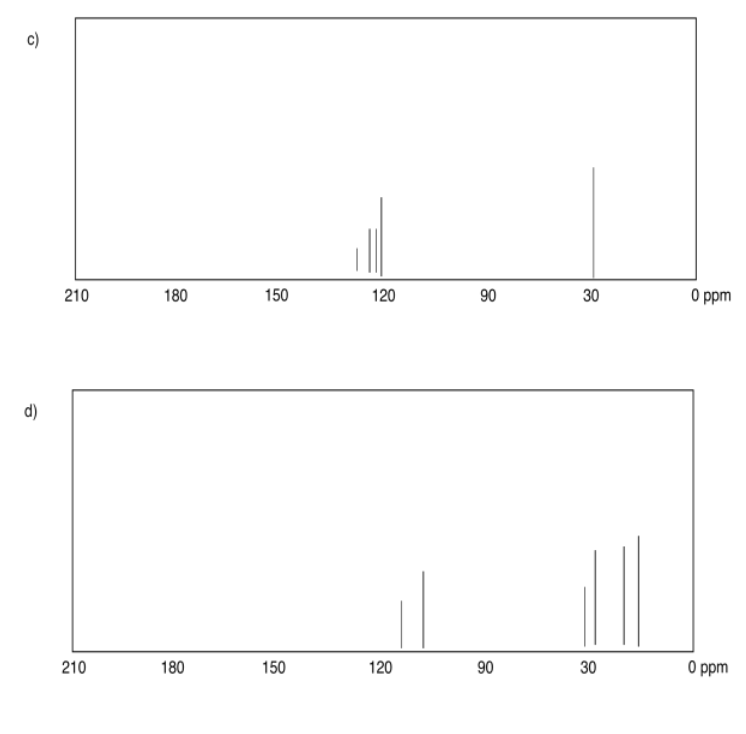
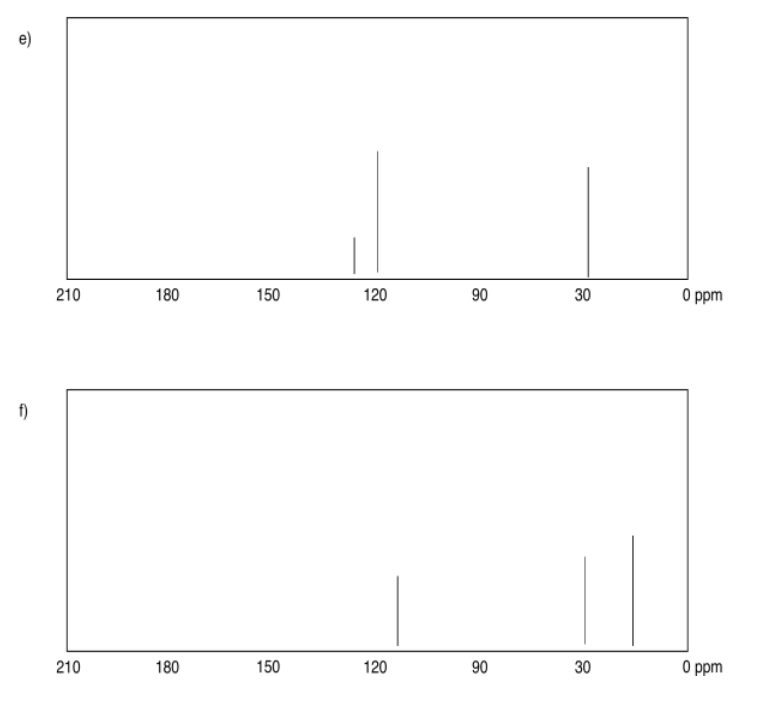
Exercise 4.4.2:
a) sp3 b) sp2 c) sp2 d) sp3 e) sp3 f) sp2
Exercise 4.5.1:
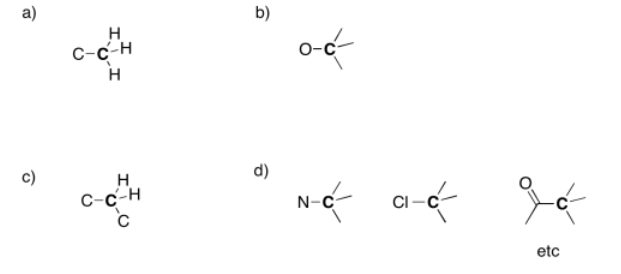
Exercise 4.5.2:
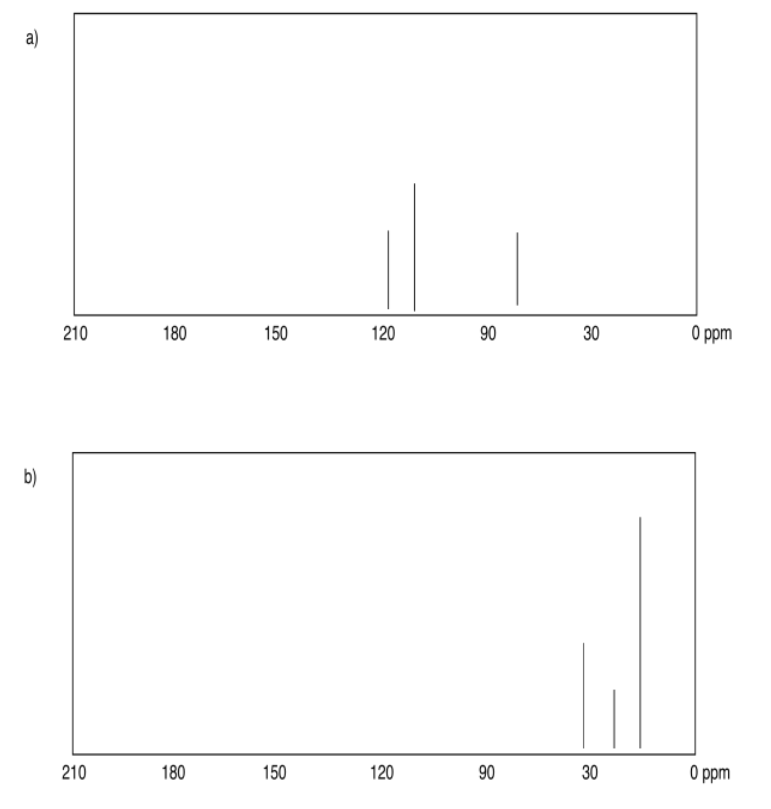
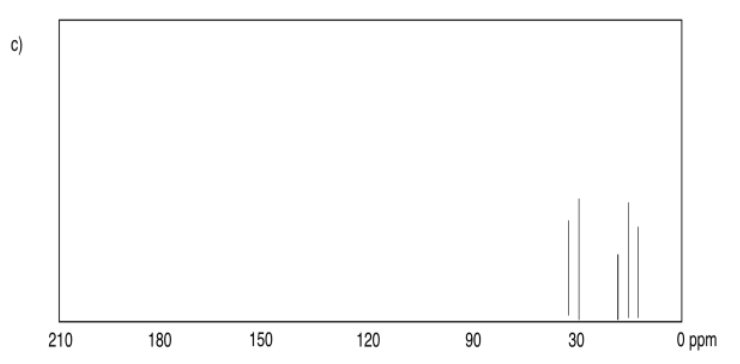
Exercise 4.6.1:
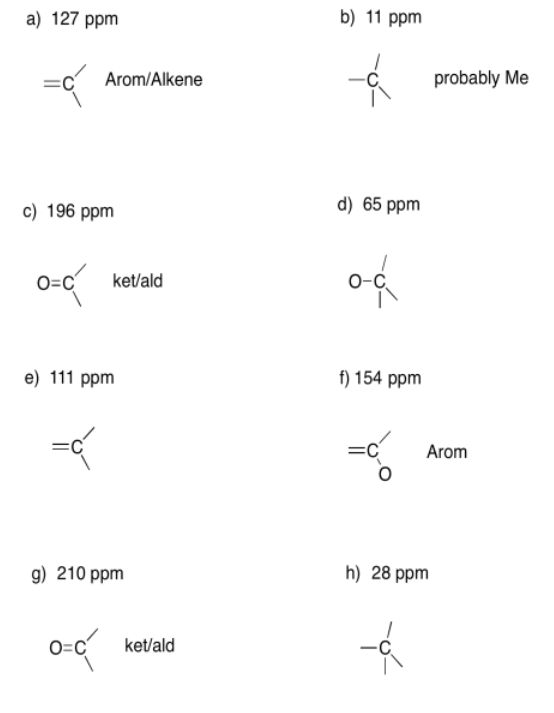

Exercise 4.6.2:
a)
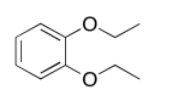
b)
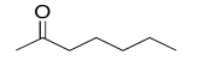
c)
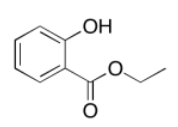
Exercise 4.8.1:
a) H-Csp3 b) H-Csp3 c) H-Csp2 d) H-Csp3 e) H-Csp2 f) H-Csp2 g) H-Csp3
Exercise 4.8.2:
a) carbon b) carbon c) nitrogen d) oxygen e) carbon f) oxygen g) nitrogen
Exercise 4.8.3:
a) aromatic b) aromatic c) alkene d) alkene e) alkene f) aromatic
Exercise 4.8.4:
a) H-CAr-C b) H-CAr-C c) H-CAr-N d) C=O e) C=O f) H-CAr-N g) H-CAr-N
Exercise 4.8.5:
- 3.4 ppm: Ha 1.5 ppm: Hb, Hc 0.9 ppm: Hd
- 7.4 ppm: Hd 6.9 ppm: Hb, Hc 3.7 ppm: Ha
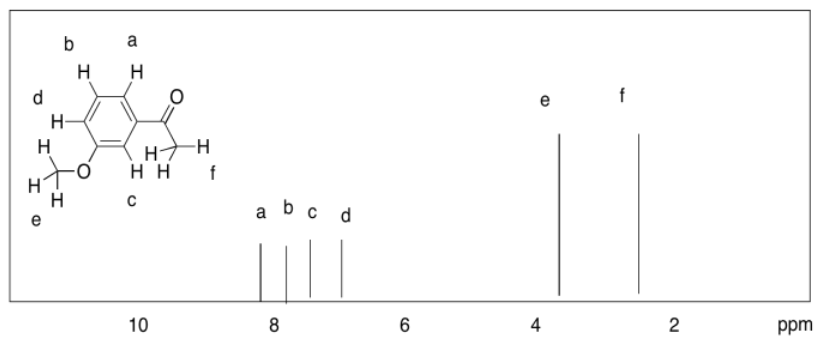
- 10.1 ppm: Ha 7.9 ppm: Hb 7.6 ppm: Hd 7.5 ppm: Hc
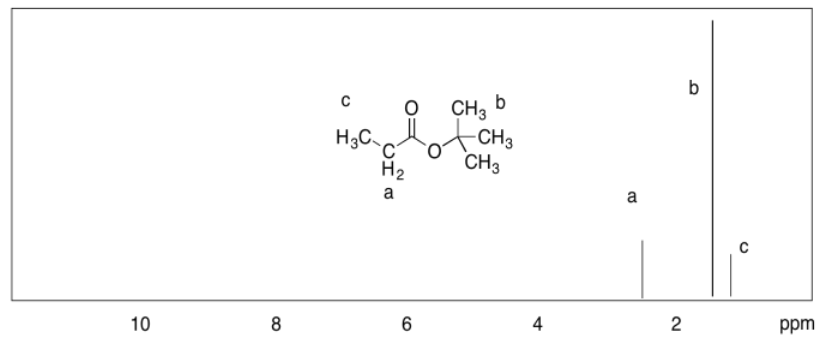
- 7.9 ppm: Hb 7.6 ppm: Hd 7.4 ppm: Hc 2.5 ppm: Ha
Exercise 4.8.6:
a)
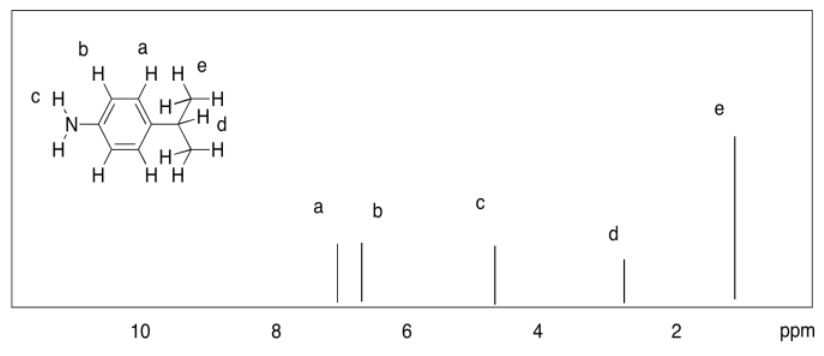
b)
c)
d)
Exercise 4.9.1:
- 0.9 ppm, 6H; 1.0 ppm, 6H (1:1 ratio)
- 0.9 ppm, 6H; 1.0 ppm, 12H (1:2 ratio)
- 0.9 ppm, 6H; 1.0 ppm, 16H (3:8 ratio)
- 0.9 ppm, 6H; 1.0 ppm, 10H (3:5 ratio)
- 0.9 ppm, 6H; 1.0 ppm, 8H (3:4 ratio)
Exercise 4.9.2:
a)
b)
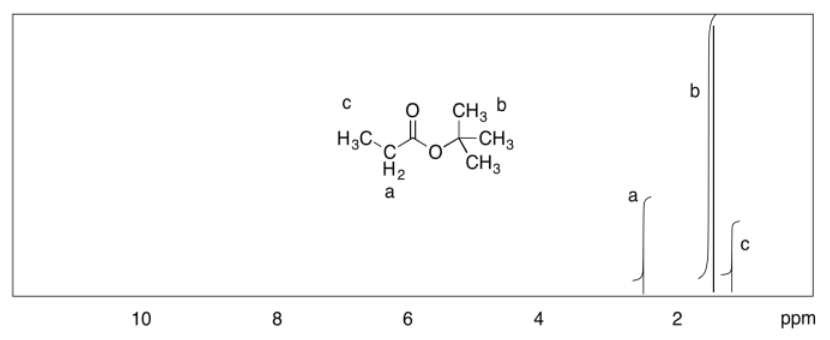
c)
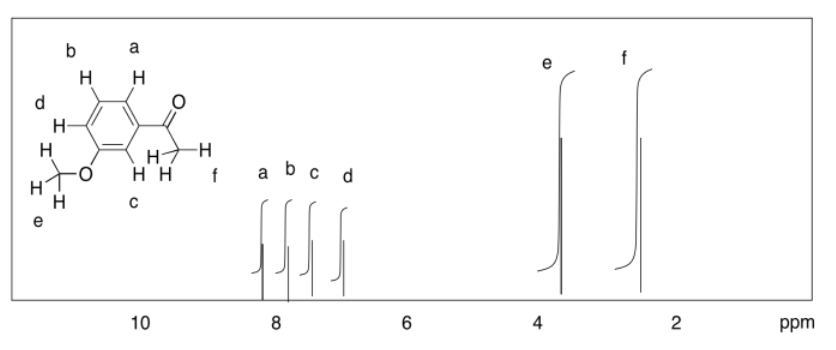
d)
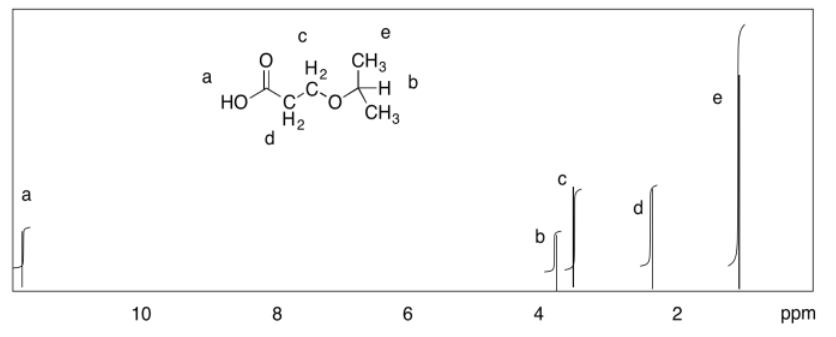
Exercise 4.9.3:
a) 5:2:3
Exericse 4.10.1:
(There will be some variation in the shift depending on the rest of the structure; this is just an estimate.)
a) 3.5 ppm, quartet, 2H b) 1.5 ppm, sextet, 2H c) 2.6 ppm, septet, 1H
d) 2.3 ppm, quintet, 1H e) 2.2 ppm, quartet, 2H f) 1.7 ppm, nonet, 1H
Exercise 4.10.2:
(There will be some variation in the shift depending on the rest of the structure; this is just an estimate.)
a) 7.8 ppm, doublet, 1H b) 8.4 ppm, singlet, 1H c) 6.7 ppm, singlet, 1H
d) 7.2 ppm, troplet, 1H e) 6.9 ppm, doublet, 1H
Exercise 4.10.3:
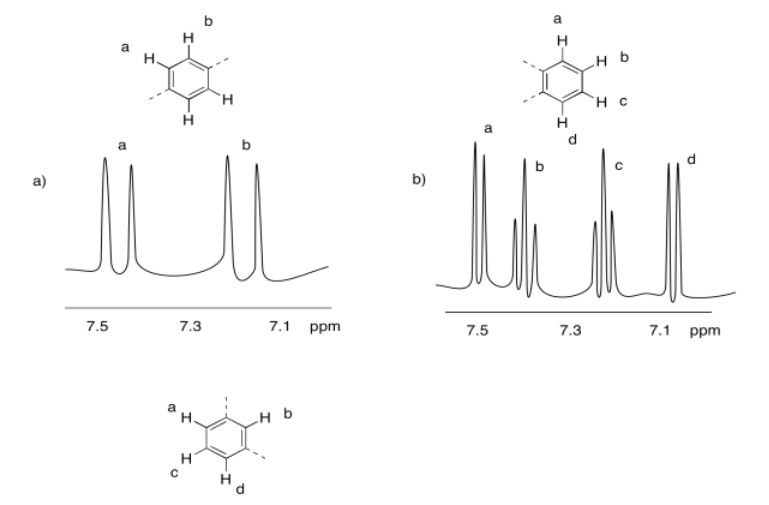
Exercise 4.10.4:
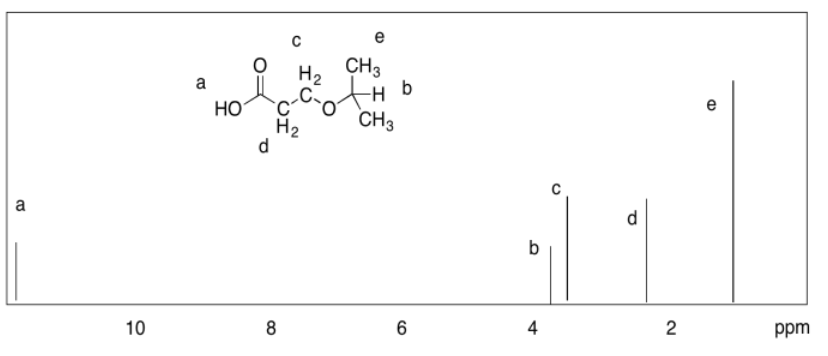
3.4 ppm, doublet: CH-CH2-O
2.1 ppm, singlet: OH
1.7 ppm, nonet: (CH3)2CHCH2
0.9 ppm, doublet: CH(CH3)2
Exercise 4.10.5:
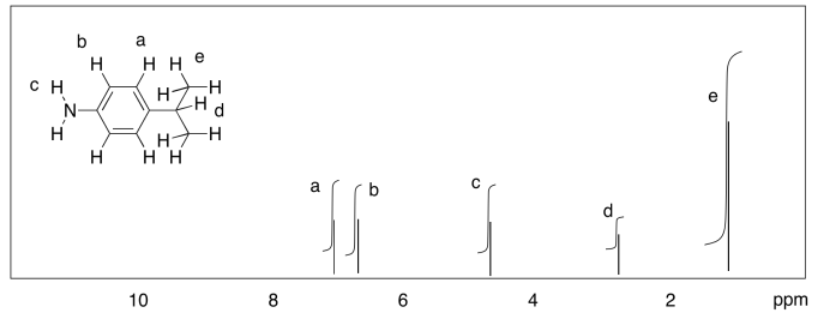
a) This is a simulated spectrum. The peaks at f, e, and c are singlets. The peak at d is a doublet. The peaks at a & b are unfortunately coincident, so their multiplicities are obscured, but they would be doublets & triplets, respectively.
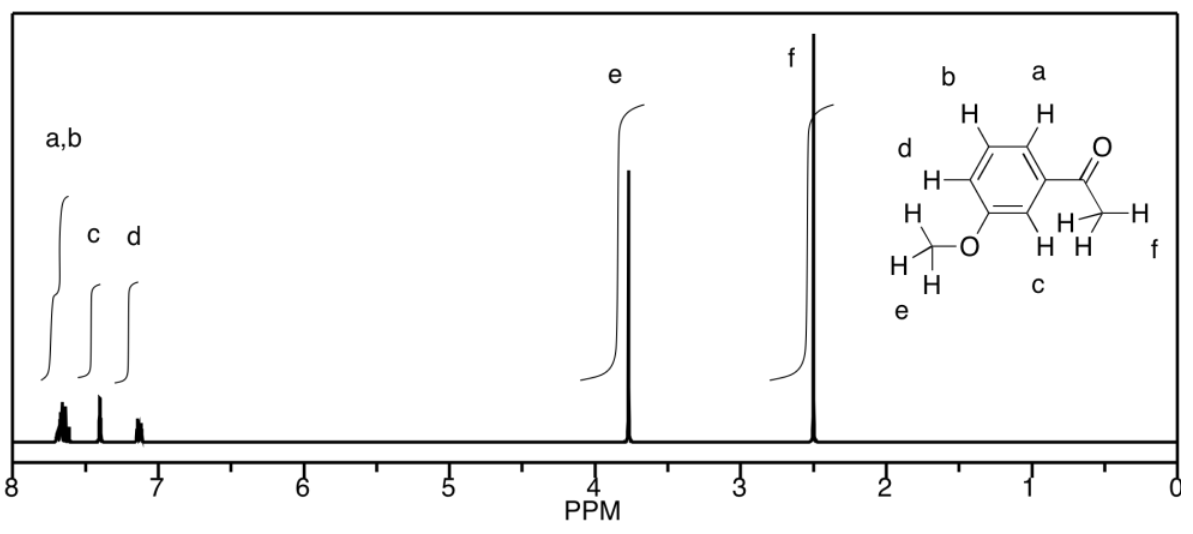
b)
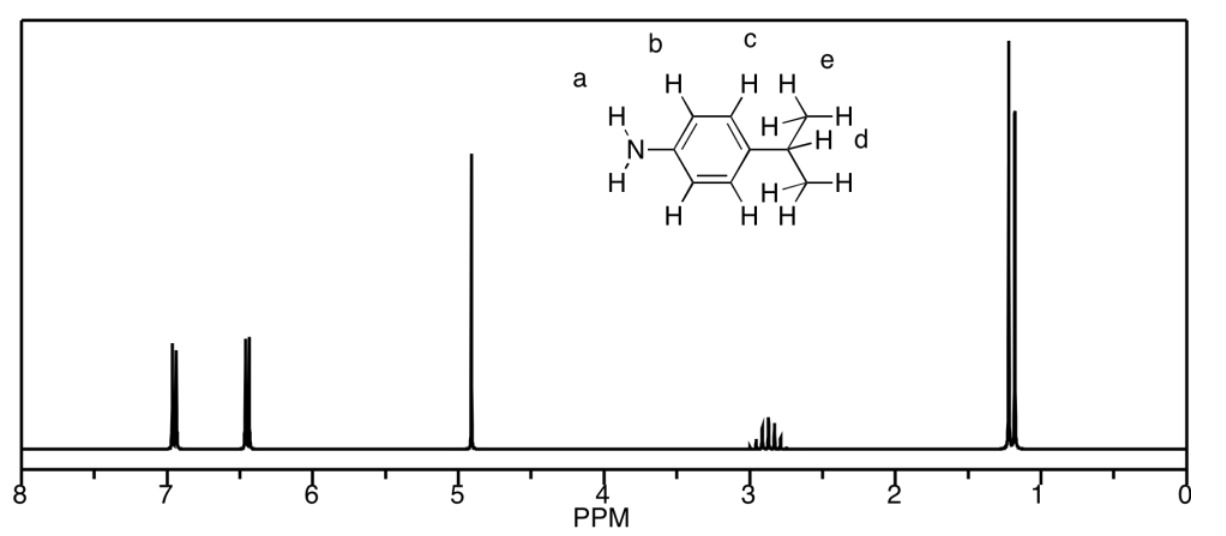
c)
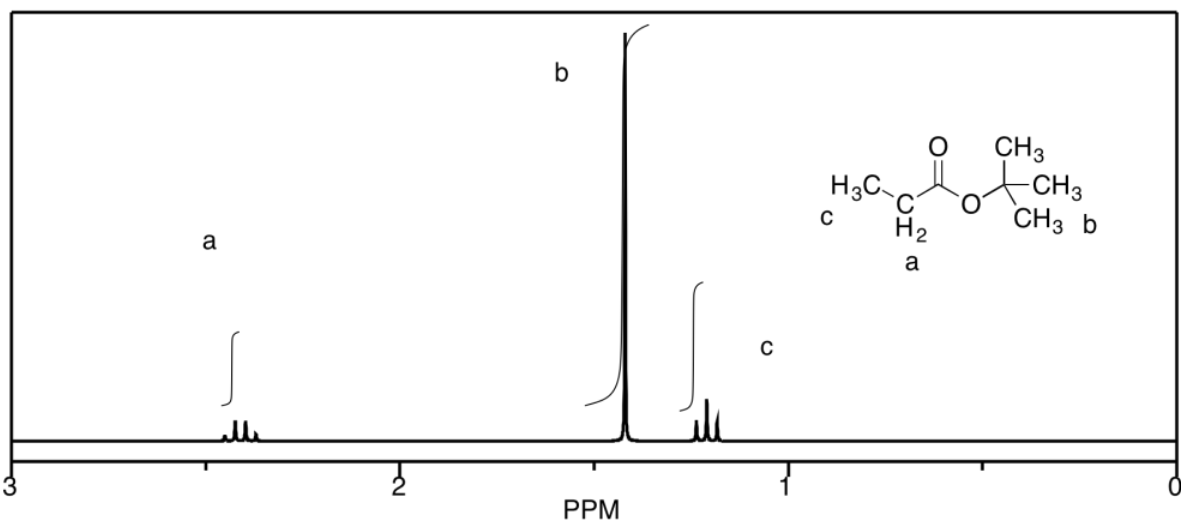
d) The peaks at b and c unfortunately coincide, but they would be a septet and a triplet, respectively. Otherwise, a is a singlet, d is a triplet, and e is a doublet.
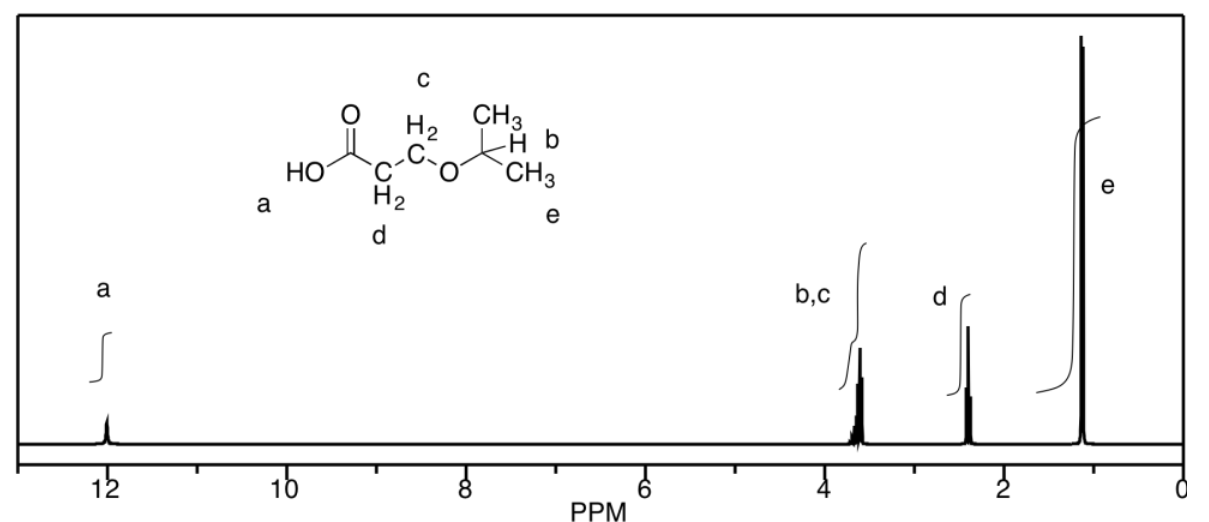
Exercise 4.12.1:
Fill in partial structures for the following peaks.
Aromatic (benzene etc) peaks are labeled "Ar" to distinguish from alkene peaks that show up further upfield (lower shift). Also, some peaks may be in two symmetric positions and are labeled with "x2".
a) 10.1 ppm, 1H, triplet, CH2-CH=O b) 3.4 ppm, 1H, septet, O-CH(CH3)2
c) 7.3 ppm, 2H, triplet, CH=CH-CH x 2 (Ar) d) 5.4 ppm, 1H, quartet, CH3-CH=C
e) 1.4 ppm, 2H, sextet, CH3-CH2-CH2 f) 8.0 ppm, 1H, singlet, C=CH-C (Ar)
g) 2.1 ppm, 3H, singlet, CH3-C=C or CH3-C=O or CH3-N; need context to choose
h) 6.8 ppm, 2H, doublet, CH=CH-C x 2 (Ar) i) 0.9 ppm, 6H, doublet, CH-CH3 x 2
Exercise 4.12.2:
Identify the errors in the following partial structures:
a) 3.6 ppm, 2H, triplet, CH2-CH2 the first carbon must be attached to O to have a shift at 3.6 ppm
b) 2.1 ppm, 2H, singlet, CH3-C=C the integral says only 2H, not 3H
c) 7.4 ppm, 2H, doublet, CH=CH2-C the shift implies aromatic, so there can only be one H per carbon; must be symmetry
d) 1.8 ppm, 2H, quintet, CH2-CH4 there can't be four hydrogens on one carbon; must be some hydrogens on each side
e) 7.8 ppm, 1H, triplet, -CH=CH2 the shift implies aromatic, so there can only be one H per carbon; must be one one each side
f) 1.7 ppm, 1H, nonet, NH2-CH(CH3)2 an attached nitrogen would shift this hydrogen past 2 ppm; also, coupling is rarely seen across O or N, so the two neighbouring H on the left are probably on a carbon
Exercise 4.13.1:
a) TBME b) acetone c) THF d) methanol e) ethyl acetate
Exercise 4.14.1:
- appearance of CH-O near 3.5 ppm (multiplet, 1H)
- appearance of CH2-O near 3.5 ppm (triplet, 2H); disappearance of =CH near 5-6 ppm (mutiplets, total 3H)
- appearance of HC=O near 10 ppm (triplet, 1H); disappearance of =CH near 5-6 ppm (mutiplets, total 3H)
- appearance of HC=O near 10 ppm (triplet, 1H); disappearance of CH2-O near 3.5 ppm (doublet, 2H)
- appearance of CH2-O near 3.5 ppm (triplet, 2H)
- appearance of CH2-O near 4 ppm (triplet, 2H)
- appearance of =CH near 5-6 ppm (mutiplets, total 2H); disappearance of HC=O near 10 ppm (triplet, 1H);
- disappearance of =CH near 5-6 ppm (mutiplets, total 2H); appearance of triplet:sextet:triplet pattern between 1-2 ppm
i) appearance of HC=O near 10 ppm (triplet, 1H); disappearance of CH2-O near 3.5 ppm (doublet, 2H)
j) appearance of CH-O near 3 ppm (singlet, 3H) and 3.5 ppm (sextet, 1H); disappearance of =CH near 5-6 ppm (mutiplets, total 2H)
Exercise 4.15.1:
a) student 1: Let's use the H2C-O peak of ethyl propanoate at 4 ppm and the acetonitrile methyl at 2 ppm. The ratio appears to be 2:1, but they represent 2 protons and 3 protons, respectively. That means the ratio of molecules is 2/2:1/3 = 3:1 ethyl propanoate : acetonitrile.
student 2: We'll use the H2C-O peak of ethyl propanoate at 4 ppm and the H2C-O peak of THF at 3.5 ppm. The ratio appears to be 3:2, but they represent 2 protons and 4 protons, respectively. That means the ratio of molecules is 3/2:2/4 = 12:4 = 3:1 ethyl propanoate : THF.
student 3: Look at the H2CCl2 peak of dichloromethane at 5 ppm and the H2C-O peak of THF at 4 ppm. The ratio appears to be 1:2, and they both represent 2 protons, so the ratio of molecules is 1:2 dichloromethane : ethyl propanoate.
b) student 1: The sample is \(\frac{1}{1 + 3} \times 100 \% = 25 \%\) acetonitrile.
student 2: The sample is \(\frac{1}{1 + 3} \times 100 \% = 25 \%\) THF.
student 3: The sample is \(\frac{1}{1 + 2} \times 100 \% = 33 \%\) acetonitrile.
Exercise 4.15.2:
The obvious NMR handles are the H-C=O aldehyde proton at 10 ppm for benzaldehyde and the alcohol-adjacent H-C-O proton at 4.5 ppm for 1-phenylpropanol.
Each of those peaks represents one proton, so the integral ratio of 1:2 suggests a ratio of bezaldehyde to 1-phenylpropanol of of 1:2. That translates into 33% benzaldehyde, 67% 1-phenylpropanol.
Exercise 4.15.3:
The NMR handles here are the H-C=O aldehyde proton at 10 ppm for benzaldehyde and the alcohol-adjacent H2C-O protons near 5 ppm for benzyl alcohol.
In this case, we need to correct for the differing numbers of protons represented by each peak: 1H for the aldehyde peak but 2H for the alcohol one. The integral ratio of 1:6 therefore suggests a ratio of bezaldehyde to 1-phenylpropanol of of 1:3. That translates into 25% benzaldehyde, 75% 1-phenylpropanol.
Exercise 4.15.4:
We could use the peak corresponding to the O-CH-C=O proton above 5 ppm for the repeat unit and the peak for the CH2-O proton in the initiator/end group near 3.5 ppm. The integral ratio is 24:1, but they represent different numbers of hydrogens, so the repeat unit to end group ratio is really 24/1:1/2, or 48:1. The degree of polymerization is 48.


