1.7: Elementary Reactions

The mechanism of a reaction is a series of steps leading from the starting materials to the products. After each step, an intermediate is formed. The intermediate is short-lived, because it quickly undergoes another step to form the next intermediate. These simple steps are called elementary reactions.

Because an overall reaction is composed of a series of elementary reaction, the overall rate of the reaction is somehow dependent on the rates of those smaller reactions. But how are the two related?

Let's look at two cases. We'll keep it simple and both cases will be two-step reactions.

The first case begins with a reaction having a pretty low activation barrier. Maybe there is a lot of bond-making involved at the beginning, so this reaction gets an easy start. However, after that, things get harder. The second step has a higher activation barrier.

Both of these reactions occur at particular rates. The first step has a low barrier, so it occurs quickly. The second step has a high barrier, so it happens only slowly.

In that case, the intermediate will be formed quickly and it will sit around for a while before the second step has a chance to happen. The second step is like a bottleneck or a traffic jam. No matter how quickly things were going in the first step, the reaction has to wait to get through the second step. The rate of the overall reaction really depends on the second step. We call this step the "rate-determining step".

Each step has its own rate constant associated with it. We'll call these constants k₁ and k₂. The lower the barrier, the faster the rate, and the larger the rate constant.

We can predict rate laws for elementary reactions (although the same thing isn't true for overall reactions). The rate law for an elementary reaction is simply its rate constant, times the concentrations of any species involved in that step.

The rate of formation of product will be determined by the rate of that second step, the rate-determining step. The rate of that second step is the rate constant, k₂, times the concentration of the intermediate.

\[\frac{d[Product]}{dt} = k_{2}[Intermediate]\]

But what is the concentration of the intermediate? The intermediate is produced in the first step, so its concentration depends on how quickly it is produced from the reactants. However, if the activation barrier is low, that first step may be reversible; it may really be an equilibrium reaction. So there is a third step in this reaction, and it goes backwards from the intermediate to the reactant. We'll call the rate constant for this step k_-1.

In terms of kinetics, an equilibrium is really just a ratio of forward and reverse steps. If the forward step is much faster, this ratio is bigger than one, and products are favored. If the reverse step is much faster, the ratio is smaller than one, and reactants are favored.

\[K_{eq} = \frac{k_{1}}{K_{-1}} = \frac{[Intermediate]}{[Reactant]}\]

Or, rearranging,

\[\frac{k_{1}}{k_{-1}} [Reactant]=[Intermediate]\]

Now we know the concentration of the intermediate. That means the rate of the overall reaction is

\[\frac{d[Product]}{dt}= \frac{k_{2}k_{1}}{k_{-1}}[Reactant]\]

The take-home lesson is this: the second step is the rate determining step, so that step tells us how quickly the product forms. However, that step depends on an intermediate formed in an earlier step, so that earlier step also influences how quickly the product forms.

• The rate-determining step controls the rate of the reaction.
• The steps prior to the rate determining step influence the rate of the reaction by supplying intermediates needed for the rate determining step.

Now let's think about the opposite case. Suppose the first step has a very high barrier and the second step has a lower one. We have to wait and wait and wait for the intermediate to be produced, but once it's there, it reacts pretty quickly to give products.

In this case, the first step is the rate-determining step. That's the step that controls the rate of the reaction. As soon as that step proceeds, the rest of the reaction can occur quickly.

In this case,

\[\frac{d[Product]}{dt} = k_{1}[Reactant]\]

• Any steps after the rate-determining step don't influence the rate of the reaction.

In some cases, we can use our judgement to try to predict which transition states are highest in energy in a multi-step mechanism. However, much of the knowledge about what is happening between the reactant and the product would really come from computational chemistry. In computational chemistry, the energies of the intermediates and the transition states can be calculated using quantum mechanics. This task is not necessarily easy.

Exercise \(\PageIndex{1}\)

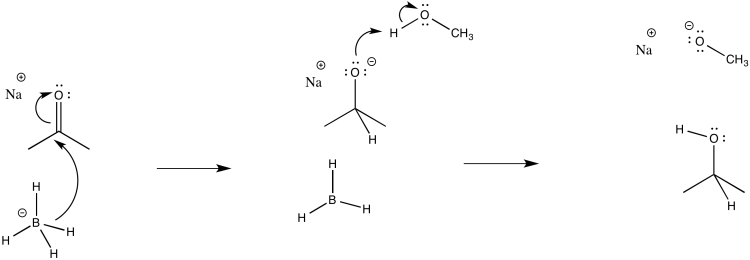
Consider the borohydride reduction of a ketone in methanol.

1. Draw a mechanism for this reaction. (If you know about the competing reaction between borohydride and methanol, ignore it. If you didn't know anything about that, forget I said anything.)
2. Assign rate constants (k₁, k₂, k₃...) for each elementary step in the reaction.
3. One of the steps along this reaction is probably reversible. Which one? Why?
4. What do you think is the rate-determining step in this reaction?
5. Draw a reaction progress diagram for this reaction.
6. Predict a rate law for this reaction.

Answer a

Answer b

The first step proceeds at k₁; the second at k₂.

Answer c

The second step is probably reversible. It is just the exchange of a proton from one OH group to another.

Answer d

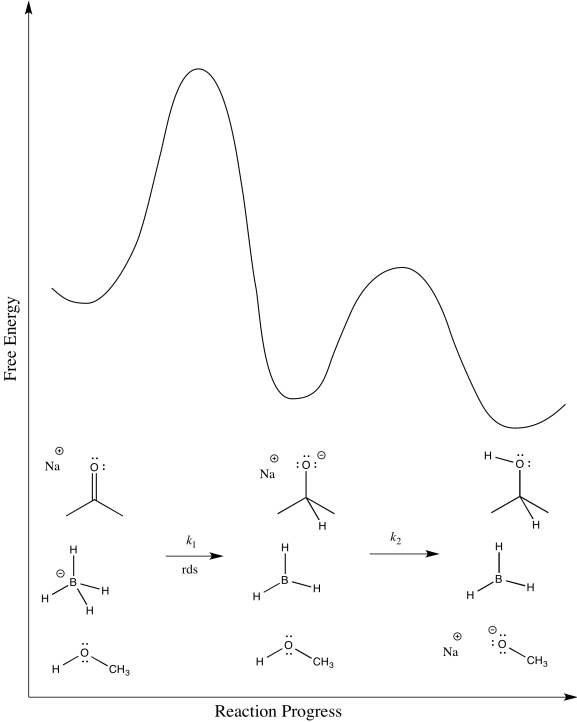
Answer e

\[Rate = k_{1}[ketone][NaBH_{4}] \nonumber\]

Exercise \(\PageIndex{2}\)

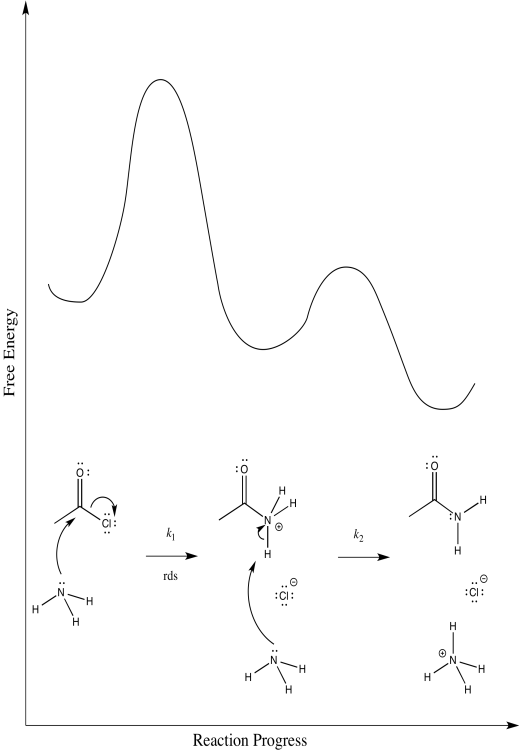
Consider the ammonolysis of acetyl chloride.

1. Draw a mechanism for this reaction.
2. Assign rate constants (k₁, k₂, k₃...) for each elementary step in the reaction.
3. Draw alternative reaction progress diagrams for this reaction. In each case, assume a different rate determining step.
4. Predict the rate law corresponding to each of your possible reaction progress diagrams. Can the rate law be used to distinguish between all of the possibilities?
5. Consider your alternative reaction progress diagrams and decide which one is most likely. Justify your choices for eliminating the other one(s).
6. Predict a rate law for this reaction.

Answer a

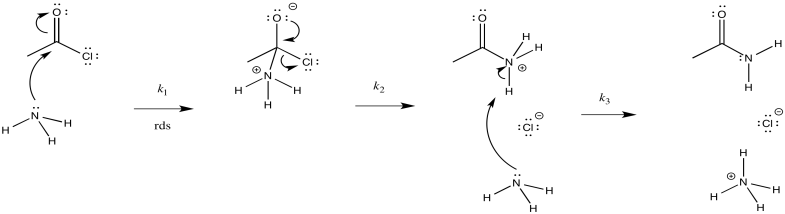
Answer b

The first step proceeds at k₁; the second at k₂; the third at k₃.

Answer c

There are three different steps, each of which might be rate determining.

The first:

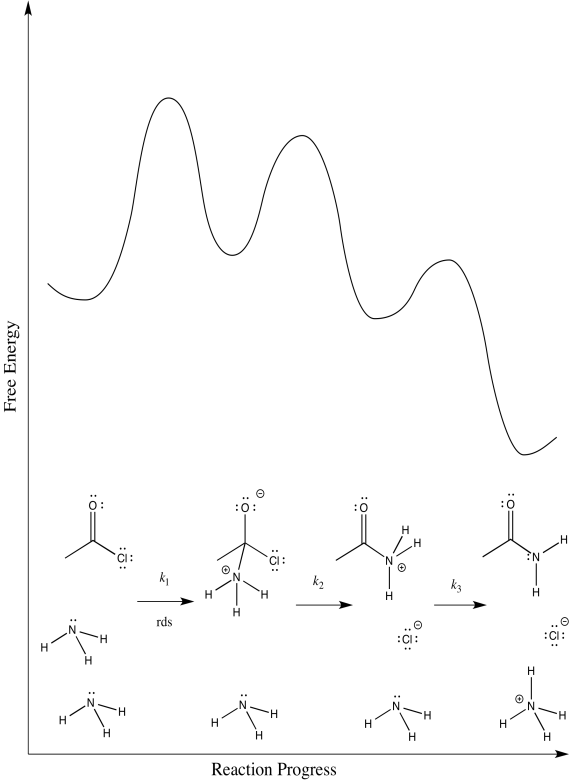
The second:

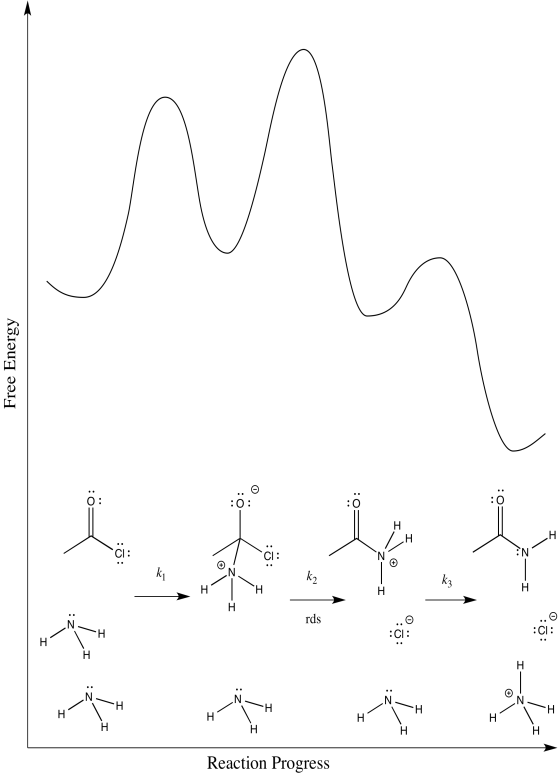
The third:

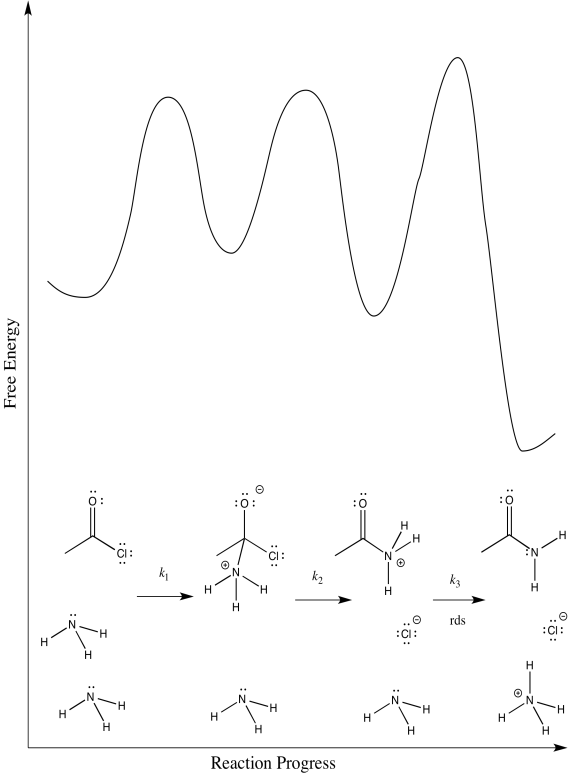
Answer d

First one: \(Rate = k_{1}[CH_{3}COCl][NH_{3}]\)

Second one: \(Rate = k_{1}k_{2}[CH_{3}COCl][NH_{3}]

Third one: \(Rate = k_{1}k_{2}k_{3}[CH_{3}COCl][NH_{3}]^{2}\)

The rate law could be used to distinguish the third from the first two. However, it would be impossible to tell the difference between the first two using the rate law alone.

Answer e

We can probably rule out the third possibility right away. Proton transfers tend to happen pretty quickly, especially in the presence of a reasonable base such as ammonia. Measuring the rate law would quickly confirm this assumption.

Scenarios 1 and 2 are much harder to distinguish. In both cases, a bond is being broken as another bond is being made. We could make an educated guess that the formation of the good chloride leaving group is pretty easy; that would make step 1 the rate determining step.

However, we are always left with some ambiguity in subtle cases like this one. In order to get a better idea about which transition states are the highest, we would have to perform computational chemistry.

Exercise \(\PageIndex{3}\)

There are two other possible mechanisms for ammonolysis of acetyl chloride. You already know they aren't the right mechanism, but let's look at the reason we know that.

1. The first possibility is that the chloride ion leaves in the first step. The ammonia comes in afterwards.
   1. Draw this mechanism.
   2. Provide a reaction progress diagram.
   3. Identify the rate determining step and the rate law.
2. The second possibility is that the chloride gets pushed out as the ammonia comes in (instead of the C=O π bond breaking). Draw this mechanism.
   1. Draw this mechanism.
   2. Provide a reaction progress diagram.
   3. Identify the rate determining step and the rate law.
3. Given the experimental rate law, \(\text{Rate} = k [\ce{CH3COCl}][\ce{NH3}]\), can either of these possibilities be ruled out?

Answer a i

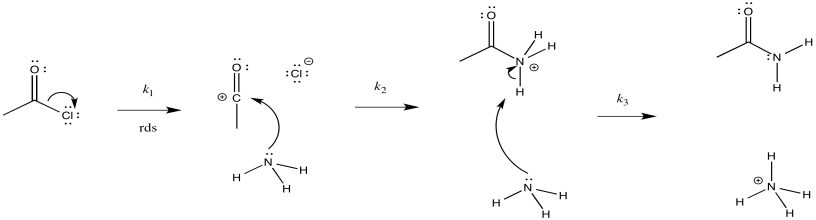
Answer a ii

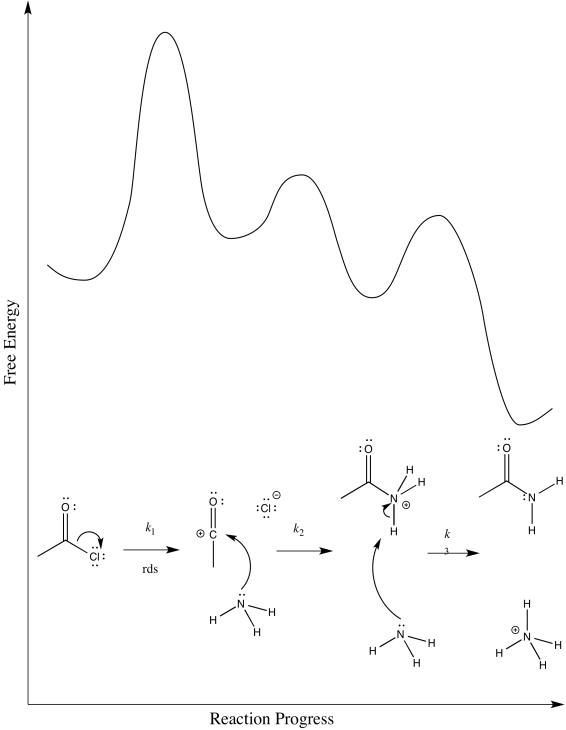
Answer a iii

\[Rate = k_{1}[CH_{3}COCl] \nonumber\]

Answer b i

Answer b ii

Answer b iii

\[Rate = k_{1}[CH_{3}COCl][NH_{3}] \nonumber\]

Answer c

On the basis of the rate law, possibility (a) can be ruled out, but not possibility (b)

Another commonly used experiment in kinetics is a kinetic isotope effect experiment. Although two isotopes of an atom have almost identical properties, the difference in mass between the two isotopes can cause subtle differences in reaction rates. For rather complicated reasons, two isotopes display different sensitivities to geometry changes that occur up to and including the rate determining step.

For example, if the carbonyl carbon in acetyl chloride is replaced by a ¹³C isotope (it is normally ¹²C), it will react at a different rate tthan the normal compound, but only if that carbon undergoes a geometry change at some point before it finishes the rate determining step. If the two compounds react at the same rate, no such geometry change has occurred.

Exercise \(\PageIndex{4}\)

The ratio of reaction rates of CH₃¹³COCl : CH₃¹²COCl is about 0.9.

1. What does this observation tell you about the mechanism?
2. Does it rule out any possibilities in Exercise \(\PageIndex{3}\)?

Answer a

There is a geometry change prior to or during the rate determining step.

Answer b

Possibility (b) can be ruled out.

Exercise \(\PageIndex{5}\)

a) Draw the product of the following reaction.

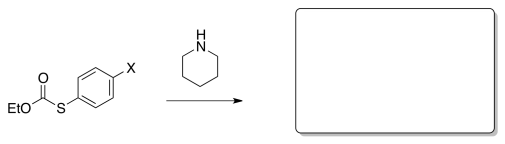
b) Provide a mechanism for the reaction.

c) Briefly describe what is meant by the term "thermodynamics" in the context of reactivity.

d) Briefly define what is meant by the term "kinetics" in this context.

e) In which step of the mechanism is ΔS positive?

f) Write a rate law for the reaction based on your mechanism.

g) What happens to reaction rate as temperature increases?

h) What does collision theory tell us about rates of reactions?

i) The following rate constants were observed for the reaction involving different substituents X.

-X	k mol L^-1 s^-1
-OCH3	0.17
-SCN	1.76

Exercise \(\PageIndex{6}\): the Bayliss-Hillman reaction

The Bayliss-Hillman reaction is used extensively in syntheses of pharmaceuticals. However there are two possible mechanisms, shown below (Price, Broadwater, Walker and McQuade, J. Org. Chem., 2005, 70, 3980-3987).

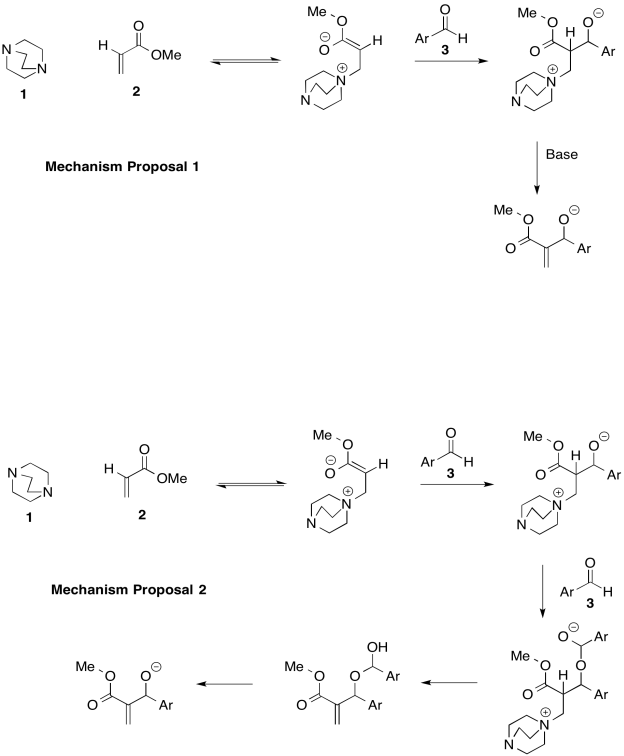
1. Provide arrows to show electron flow for each mechanism.
2. Provide a rate law for each mechanistic proposal, based on concentrations of compounds 1, 2, and 3.
3. Indicate the order in each compound based on the graphs below.

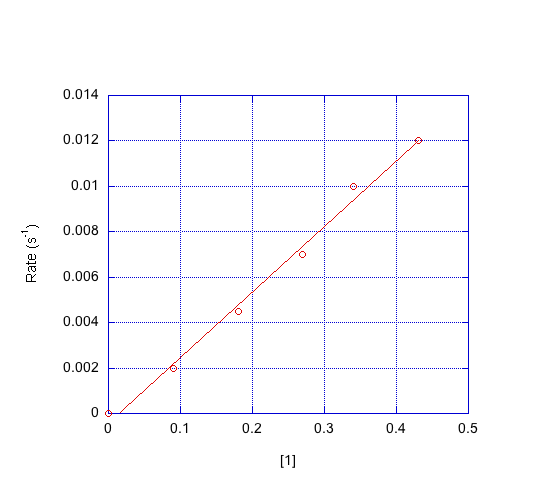
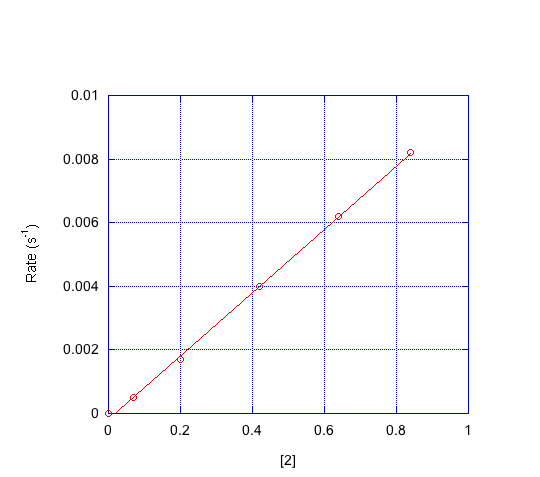
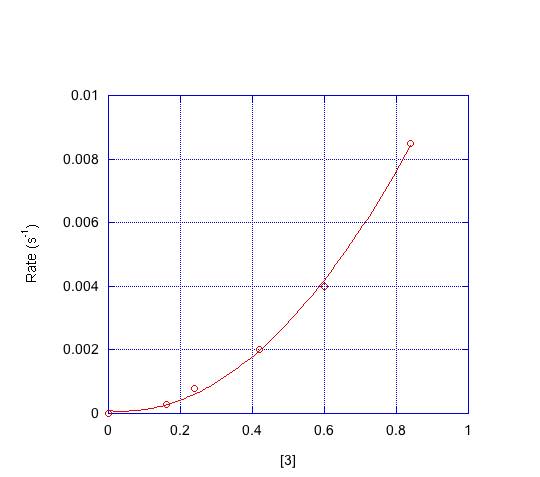
d) Which mechanism is consistent with the data?

Answer a

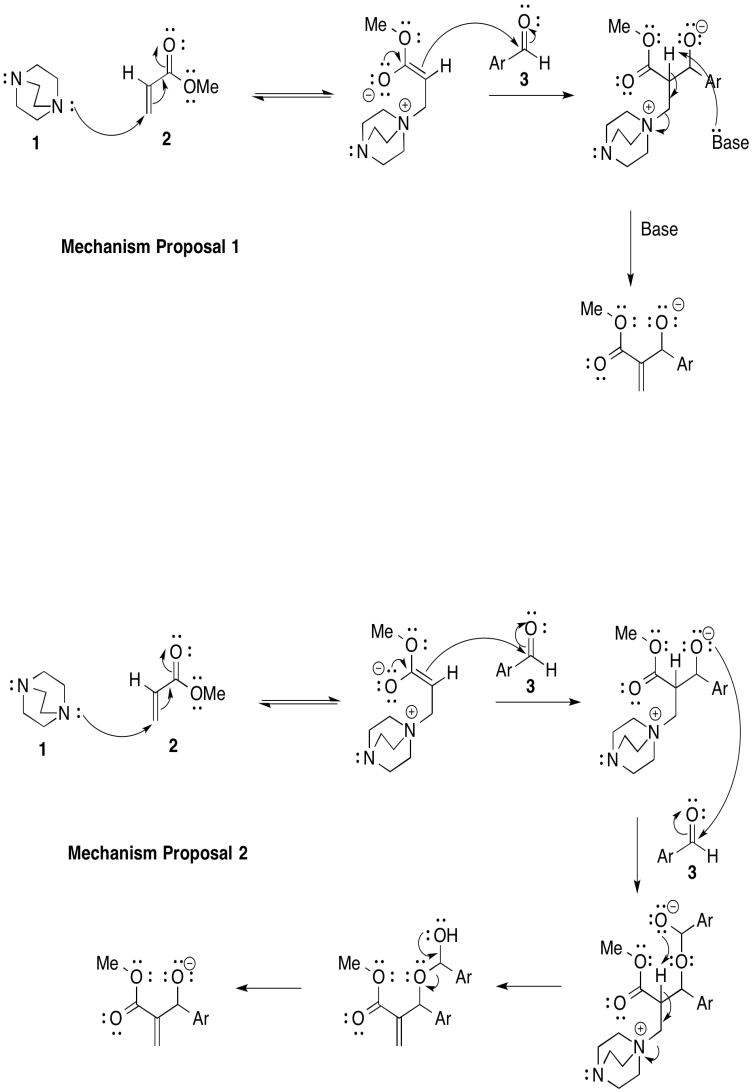
Answer b

Mechanism 1: k [1][2][3]

Mechanism 2: k [1][2][3]²

Answer c

First order in [1]; first order in [2]; second order in [3]

Answer d

Mechanism 2.