2.2: How Tightly Do Ligands Bind?
- Page ID
- 189926
All Lewis acid-base complexes form reversibly. That means that, just as the Lewis base can donate its electrons to the acid, it can take them back again.
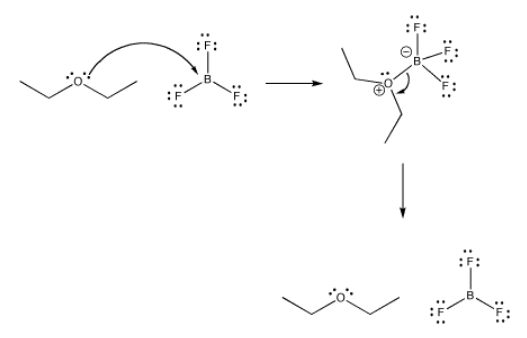
Exactly how reversible are these bonds? How tightly is a ligand bound in a coordination complex? There are many factors that affect the answer to this question, including the nature of the metal, the ligand, the environment or solvent, the temperature, and so on. However, in general, the answer could be found in any specific case by looking at an equilibrium constant.
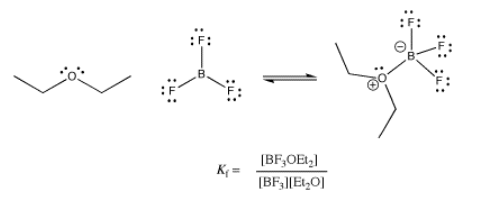
This equilibrium constant, which compares the ratio of complex to free Lewis acid and Lewis base, is sometimes called the formation constant or the binding constant. It is a measure of how tightly the ligand is bound. The same thing expressed in reverse, \(K= \frac{[BF_{3}][Et_{2}O]}{[BF_{3}OEt_{2}]}\), is called the dissociation constant. Of course, it really measures the same thing from the opposite point of view: how easily is the ligand given up? Numerically, it is just the inverse, 1 / Kf.
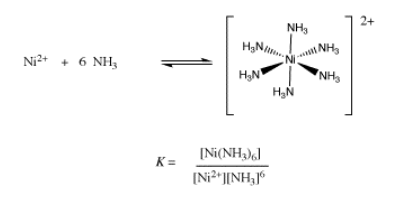
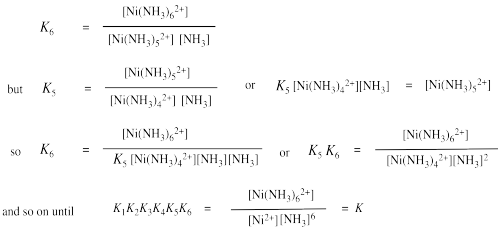
If there are many ligands bound to the ion, as in the formation of hexaammine nickel ion, then the formation constant becomes more complicated. It is really a combination of six different binding constant: the constant for the first ammonia with nickel ion, the constant for the second ammonia with the ammine nickel ion, and so on. When all of these individual constants are combined, we arrive at an ammonia concentration raised to the sixth power in the expression for the formation constant.
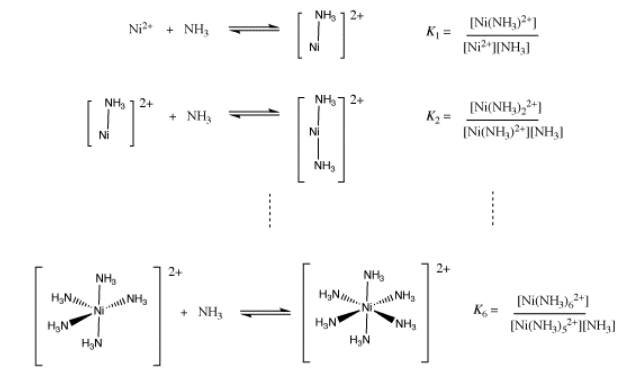
Show that the overall equilibrium constant for formation of Ni(NH3)62+ is a product of the equilibrium constants for individual ammonia binding steps, K1 x K2 x ... x K6.
- Answer
-
Determining an equilibrium constant requires that the concentrations of the individual species can be measured, such as [Ni2+], [NH3] and [Ni(NH3)62+]. This measurement might be accomplished using spectroscopic or electrochemical techniques. This measurement has been done for this example at 25 ° C in water, and the value of K = 1.0 x 108 M-6.
The numerical values for individual binding constants for ammonia with nickel at 25 ° C in water are as follows:
K1: 4.7 x 102 K2: 1.3 x 102 K3: 41 K4: 12 K5: 4.2 K6: 0.81
a) Use these values to confirm the value of the complex formation constant for [Ni(NH3)62+].
b) What explanations can you offer for the trend in individual K values?
- Answer
- Answer a
-
K = K1 x K2 x K3 x K4 x K5 x K6
= 470 x 130 x 41 x 12 x 4.2 x 0.81
= 1.03 x 108
- Answer b
-
As the nickel binds ammonia ligands, it becomes more electronically saturated. That means it becomes less Lewis acidic. It does not have as strong an attraction for additional ligands.
The reality of the experimental determination of the binding constant is more complex than illustrated in these figures. For example, a Ni2+ ion does not really exist on its own. First of all, there must be counterions involved. If the counterions are not selected carefully, they might affect the measurements. For example, if the counterions are chlorides, maybe they could form NiCl2 or other chloride species. Chloride is a Lewis base and it could compete with ammonia as an alternative nucleophile or ligand. Other counterions are called "non-coordinating" because they do not generally bind with Lewis acids; these include BF4-, PF6- and ClO4-.
In addition, the fact that the experiment was done in water means that Ni2+ ion was not really involved. Water is a nucleophile, too. That means that the real starting species was [Ni(OH2)62+]. Instead of just binding to a bare nickel ion, the ammonia was replacing the water molecules, one at a time.
Exactly how one nucleophile substitutes for another in a coordination complex is the subject of another chapter.
Explain the differences between formation constants for the following of complexes at 25 ° C:
a) [Zn(NH3)42+]: 7.8 x 108 and [Zn(CN)42-]: 4.7 x 1019
b) [Fe(CN)64-]: 1.0 x 1024 and [Fe(CN)63-]: 1.0 x 1031
- Answer
- Answer a
-
This is a Zn2+ ion binding to either NH3 or CN- ligands. The zinc cation is more strongly attracted to the anionic cyanide ligands than the neutral ammonia ligand, so the binding constant with cyanide is higher than with ammonia.
- Answer b
-
Both cases involve cyanide ions. In one case, the CN- binds to Fe2+, whereas the other case involves Fe3+. The ligand is more attracted to the more highly charged ion, so the binding constant is higher.


