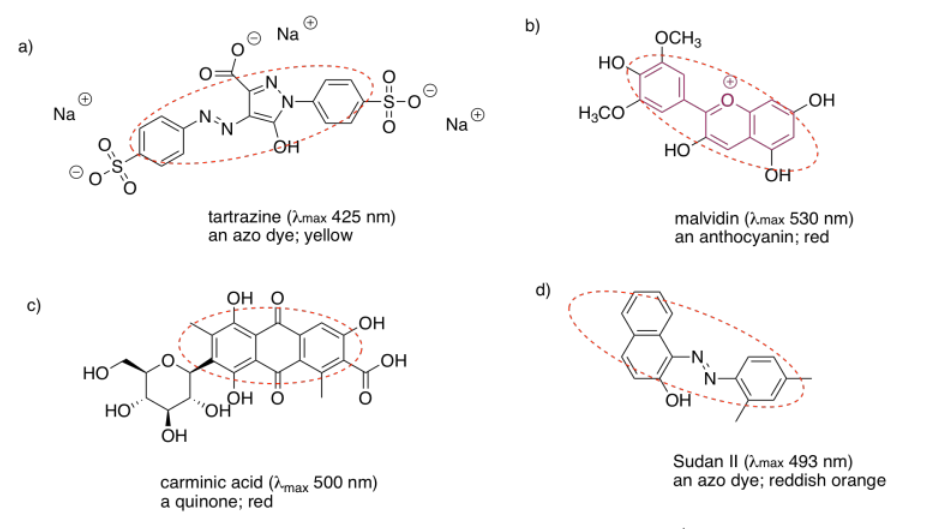
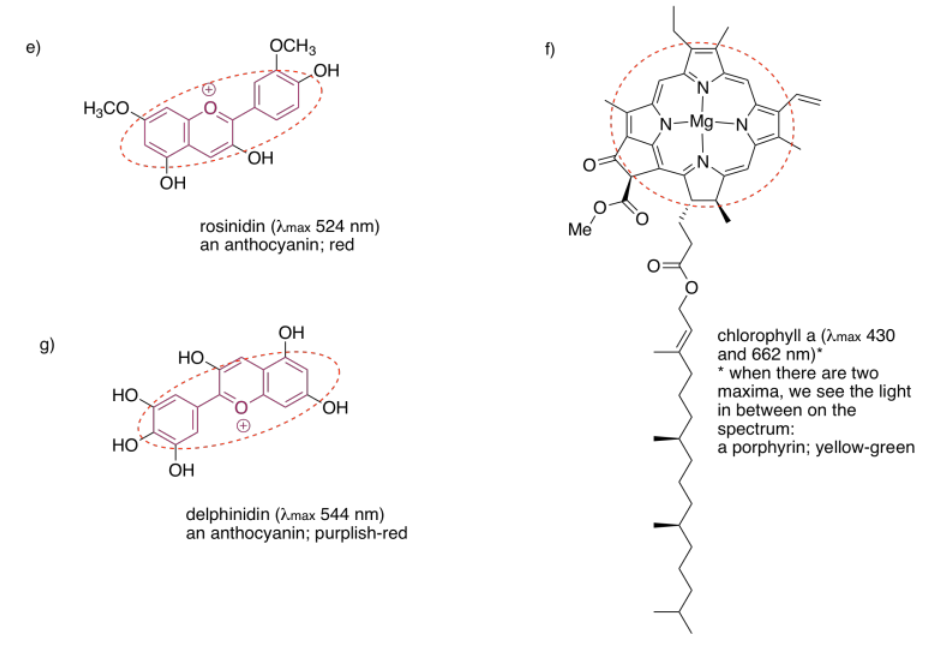
2.4: UV-Visible Spectroscopy- Solutions.

Last updated
Save as PDF

Page ID: 189757

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Exercise 2.1.1

You observe a colored object. Estimate the wavelength of light that was absorbed by the object.

a) 700 nm (just an estimate, but maybe somewhere between 620 and 750 nm)

b) 425 nm c) 540 nm d) 580 nm

Exercise 2.1.2:
a) 590 nm b) 400 nm c) 500 nm d) 300 nm

Exercise 2.1.3

a) 590 nm (strong); that's all b) 400 nm (strong); 600 nm (weak)

c) 500 nm (strong); 350 nm (weak) d) 300 nm (strong); 450 nm (weak)

Exercise 2.1.4

Remember, here we are observing the photons directly, rather than the onew complementary to the absorbed photons.

copper > barium > sodium > calcium > lithium

Exercise 2.2.1:

270 nm (strong, MLCT); 500 nm (weak, d-d)
< 200 nm* (very strong, MLCT); 275 nm (strong, MLCT); 400 nm (weak, d-d) *can't see exactly where because the peak is so tall that we can't see the top
< 200 nm* (very strong, MLCT); 275 nm (strong, MLCT); 660 nm (weak, d-d)
< 250 nm (strong, MLCT); 300 nm (strong, MLCT); 620 nm (weak, d-d)

Exercise 2.2.2:

absorbs blue-green; we see orange-red
absorbs violet; we see yellow
absorbs red; we see green
absorbs orange; we see blue

Exercise 2.2.3:

a) \(A= \varepsilon c l = 14 L g^{-1} cm^{-1} \times 0.025 g L^{-1} \times 1 cm = 0.35\)

a) \(A= \varepsilon c l = 14 L g^{-1} cm^{-1} \times 0.011 g L^{-1} \times 1 cm = 0.15\)

Exercise 2.2.4:

\(A = \varepsilon c l \: or \: c = \frac{A}{\varepsilon l} = \frac{0.75}{14 L g^{-1} cm^{-1} \times 1cm} = 0.054 g L^{-1}\)
\(A = \varepsilon c l \: or \: c = \frac{A}{\varepsilon l} = \frac{0.21}{14 L g^{-1} cm^{-1} \times 1cm} = 0.015 g L^{-1}\)

Exercise 2.2.5:

Based on our color wheel it absorbs both yellow and green; we see a mix of violet and red. (KMnO₄ is really a deep purple.)

Exercise 2.2.6:

KMnO₄ has MW = 158 g mol^-1

\[14 \frac{L}{g \: cm} \times 158 \frac{g}{mol} = 2212 \frac{L}{mol \: cm} \nonumber\]

Exercise 2.2.7:

a) \(A = \varepsilon c l = 2200 L mol^{-1} cm^{-1} \times 0.00015 mol L^{-1} \times 1cm = 0.33\)

b) \(A = \varepsilon c l = 2200 L mol^{-1} cm^{-1} \times 0.00009 mol L^{-1} \times 1cm = 0.20\)

Exercise 2.2.8:

\(A = \varepsilon c l \: or \: c = \frac{A}{\varepsilon l} = \frac {0.47}{2200 L mol^{-1} cm^{-1} \times 1 cm} = 2.1 \times 10^{-4} mol L^{-1}\)
\(A = \varepsilon c l \: or \: c = \frac{A}{\varepsilon l} = \frac {0.89}{2200 L mol^{-1} cm^{-1} \times 1 cm} = 4.1 \times 10^{-4} mol L^{-1}\)

Exercise 2.3.1:

a) blue b) orange

Exercise 2.3.2:

Add another 30 or 40 nm and you get to 270 or 280 nm.

Exercise 2.3.3:

a) about 250 nm b) about 280 nm

Exercise 2.3.4:

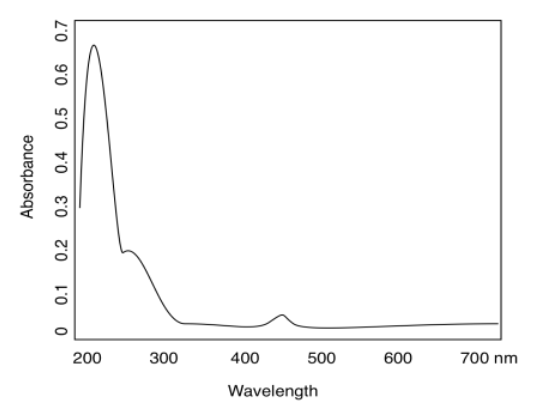
b) yellow

Exercise 2.3.5: