2.2: UV-Visible Spectroscopy - Metal Ions

Transition metals are often associated with brightly-colored compounds. Because of their relatively low electronegativity, transition metals are frequently found as positively-charged ions, or cations. In solution, metal ions would not swim around by themselves, but would attract other molecules to them. These molecules bind to the metal ions, forming coordination complexes.

These transition metal complexes or coordination complexes have lots of electrons, and they can often interact with lots of different photons. When they do, there are a number of possible electronic transitions that can result. These transitions might involve the metal ion itself, or the ligands -- those molecules or ions that bind to the metal ion.

One very common transition is called a charge transfer transition. It involves the excitation of an electron from the ligand to the metal, or vice versa. Sometimes the former case is referred to as a ligand-to-metal charge transfer, or LMCT; the latter case would be a metal-to-ligand charge transfer, or MLCT. However, these two acronyms are sometimes used interchageably to suggest some sort of transition that involves both the ligand and the metal, without worrying too much about the direction.

In addition, sometimes electrons can be excited from one level to another, just on the metal ion. For transition metals, these electronic excitations are called d-d transitions. For transition metals, the valence electrons are in the d sub-shell, and in a d-d transition, the electron is excited from one d level to another. That sounds like it might be pretty easy -- the electron isn't going very far, after all -- but d-d transitions are actually quite inefficient. The electronic transitions involved just are not very good at capturing photons.

By comparison, it might sound like it would be difficult to move an electron from the metal all the way to the ligand, but it's actually pretty easy. These electronic transitions interact with photons very efficiently.

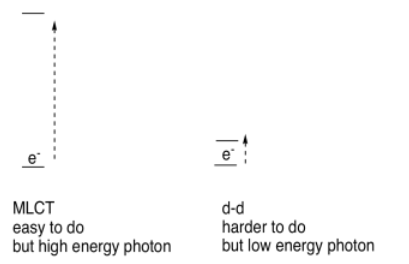
As a result, there is a kind of counterintuitive relationship in the UV-visible spectra of transition metal complexes: d-d transitions require very little energy but occur relatively infrequently, meaning they give very weak absorbances in the spectrum. MLCT transitions require much more energy but they happen frequently, leading to stronger absorbances in the spectrum.

We aren't going to worry about why different electronic transitions occur with greater or lesser efficiency; that has to do with symmetry and group theory, and some mathematics that we aren't equipped to handle right now. We just need to understand that these distinctions can influence what UV spectra look like.

Exercise \(\PageIndex{1}\)

Propose a formula for a simple, single-chain inosite containing only sodium counterions.

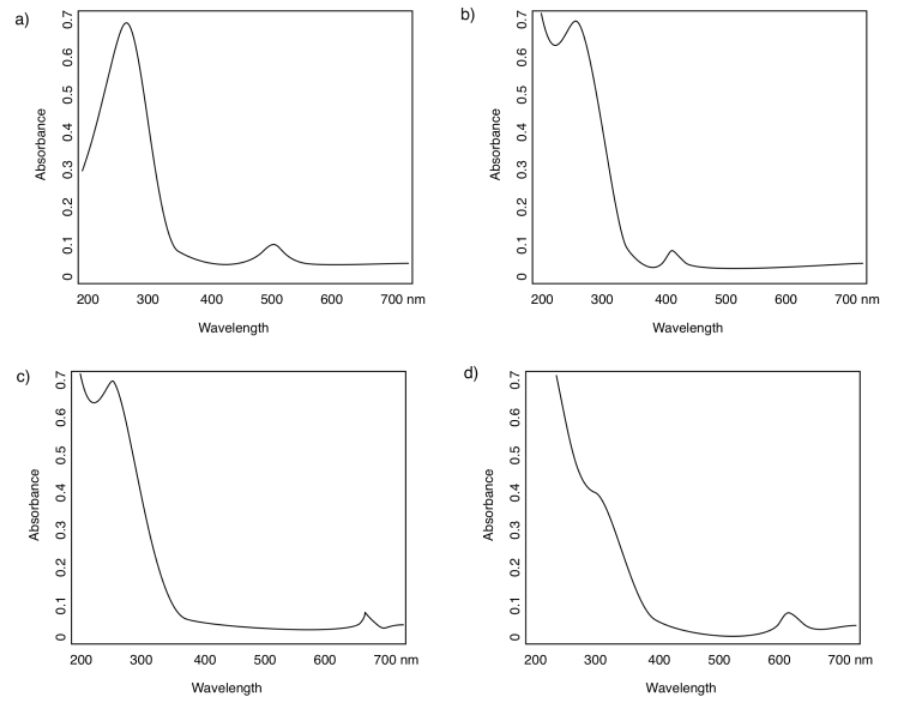
In the following spectra, assign the observed "peaks" or absorbance bands to MLCT or d-d transitions.

Answer

a) 270 nm (strong, MLCT); 500 nm (weak, d-d)

b) < 200 nm* (very strong, MLCT); 275 nm (strong, MLCT); 400 nm (weak, d-d) *can't see exactly where because the peak is so tall that we can't see the top

c) < 200 nm* (very strong, MLCT); 275 nm (strong, MLCT); 660 nm (weak, d-d)

d) < 250 nm (strong, MLCT); 300 nm (strong, MLCT); 620 nm (weak, d-d)

Exercise \(\PageIndex{2}\)

In the preceding spectra, predict the observed color of each of the complexes.

Answer

a) absorbs blue-green; we see orange-red

b) absorbs violet; we see yellow

c) absorbs red; we see green

d) absorbs orange; we see blue

The whole idea of UV spectroscopy is that different compounds might absorb photons of different wavelengths based on their electronic structures. We might be able to look at the UV spectrum of a compound and tell its identity or structure; that task would be especially straightforward if we had a few different options to choose from.

Now we see that the y axis also matters to some extent. A specific compound might absorb at 250 nm and at 450 nm; however, an additional characteristic of that compound might be that it absorbs very strongly at 250 nm and only weakly at 450 nm. Knowing that information might help us distinguish the spectrum of that compound from the spectrum of another that has similar absorption wavelengths, but that shows peaks in the UV spectrum of very different sizes.

How strongly a compound absorbs photons at a particular wavelength is described by a quantity called the extinction coefficient (or alternatively, in different variations, the absorption coefficient or the molar absorptivity coefficient).

For example, it can be shown that aqueous potassium permanganate, KMnO₄, at its absorption maximum of 530 nm, has an extinction coefficient ε = 14 L g^-1 cm^-1. How much light is absorbed by a sample of potassium permanganate at that wavelength depends on a couple of additional factors, however. First of all, how concentrated is the sample? The more potassium permanganate there is dissolved in the sample, the more light it can absorb. Also, the longer the light travels through the cuvette, the more permanganate it will encounter, and so the more light it will absorb.

So absorbance can be described as

\[A= \varepsilon c l\]

in which \(ε\) = extinction coefficient, \(l\) = path length, \(c\) = concentration.

Most cuvettes are 1 cm wide; if the extinction coefficient contains a unit of cm^-1, we can just use b = 1 cm and that part is taken care of. From there, the absorbance will just depend on the concentration of the permanganate.

Exercise \(\PageIndex{3}\)

Calculate the absorbance at 530 nm for the following concentrations of potassium permanganate in a 1 cm cuvette.

a) 0.025 g /L b) 0.011 g/L

Answer

a) A = ε c l = 14 L g^-1 cm^-1 x 0.025 g L^-1 x 1 cm = 0.35

a) A = ε c l = 14 L g^-1 cm^-1 x 0.011 g L^-1 x 1 cm = 0.15

Exercise \(\PageIndex{4}\)

Calculate the concentration of potassium permanganate (in g/L) given the following absorbance readings at 530 nm in a 1 cm cuvette.

a) A = 0.75 b) A = 0.21

Answer

a) A = ε c l or c = A / ( ε l ) = 0.75 / (14 L g^-1 cm^-1 x 1 cm) = 0.054 g L^-1

b) A = ε c l or c = A / ( ε l ) = 0.21 / (14 L g^-1 cm^-1 x 1 cm) = 0.015 g L^-1

Exercise \(\PageIndex{5}\)

Although the maximum absorption is around 530 nm, the visible absorption band in potassium permanganate actually stretches from 500 to 600 nm. What colour is potassium permanganate?

Answer

Based on our colour wheel it absorbs both yellow and green; we see a mix of violet and red. (KMnO₄ is really a deep purple.)

Frequently, extinction coefficients have units of L mol^-1 cm^-1 or M^-1 cm^-1. In these cases, the concentration is measured in mol L-1 rather than g L-1. The molecular weight (molar mass) of the compound, in g mol^-1, is the conversion factor between one unit and the other. For example, the extinction coefficient for the 530 nm peak of potassium permanganate is approximately 2 200 L mol^-1 cm^-1.

Exercise \(\PageIndex{6}\)

Confirm that the two extinction coefficients for potassium permanganate, given with different units, are actually equivalent.

Answer

KMnO₄ has MW = 158 g mol^-1

14 L g^-1 cm^-1 x 158 g mol^-1 = 2212 L mol^-1 cm^-1

Exercise \(\PageIndex{7}\)

Calculate the absorbance at 530 nm for the following concentrations of potassium permanganate in a 1 cm cuvette.

a) 1.5 x 10^-4 mol /L b) 9.0 x 10^-5 mol/L

Answer

a) \(A = \varepsilon c l = 2200 \frac{L}{mol \: cm} \times 0.00015 \frac{mol}{L} \times 1 cm = 0.33\)

b) \(A = \varepsilon c l = 2200 \frac{L}{mol \: cm} \times 0.00009 \frac{mol}{L} \times 1cm = 0.20\)

Exercise \(\PageIndex{8}\)

Calculate the concentration of potassium permanganate (in mol/L) given the following absorbance readings at 530 nm in a 1 cm cuvette.

a) A = 0.47 b) A = 0.89

Answer

a) \(A = \varepsilon c l \: or \: c = \frac{A}{\varepsilon l} = \frac{0.47}{2200 \frac{L}{mol \: cm} \times 1cm} = 2.1 \times 10^{-4} \frac {mol}{L}\)

b) \(A = \varepsilon c l \: or \: c \frac{A}{\varepsilon l} = \frac{0.89}{2200 \frac{L}{mol \: cm} \times 1cm} = 4.1 \times 10^{-4} \frac{mol}{L}\)

See additional discussion of coordination complexes.