Diffusion and Effusion
- Page ID
- 53627
Skills to Develop
- Describe the interactions involved with effusion and diffusion
In this section we discuss movements of gases. This is actually a very complicated field (called fluid dynamics) and we will not go very deep.
Effusion
Effusion is the movement of a gas through a tiny hole into a vacuum. We want to know the rate of effusion, which is how much gas moves through the hole per unit time. We assume that the gas particles don't bump into each other while they move through the hole (this means it's a narrow hole in a thin wall). So the rate of effusion just depends on how often the particles bump the hole. This depends on their density and speed. Because at a given temperature, all gases have the same kinetic energy, their speed is inversely proportional to m1/2, the square root of the mass. Thus, the relative effusion rates for different gases at the same temperature is
\[\frac{Effusion\; rate\; for\; gas\; 1}{Effusion\; rate\; for\; gas\; 2} = \frac{M_{2}^{\frac{1}{2}}}{M_{1}^{\frac{1}{2}}}\]
where M1 and M2 are the molecular weights of gas 1 and gas 2.
Diffusion
Diffusion is a more complicated process. It means the movement of gases through each other or the spreading of one gas through another. Because there are many collisions, the gases move much slower than we might expect from the average speeds near 400-700 m/s. (This is why it will take a moment to smell perfume when someone walks into a room.) Technically, many processes that sound like this are not exactly simple diffusion. We have to be careful about whether there are pressure differences or flows of gases (like wind). If there are then the process isn't simple diffusion and it won't follow the equations for simple diffusion perfectly. (The equation for simple diffusion is the same as for effusion, but for different reasons, see below.) For our purposes, when you want to predict relative rates of movement of gases, you can start with the effusion/diffusion equation. It will be exactly right in a few situations, and close enough in some others. The other situations you can study in a more advanced class if you are interested.
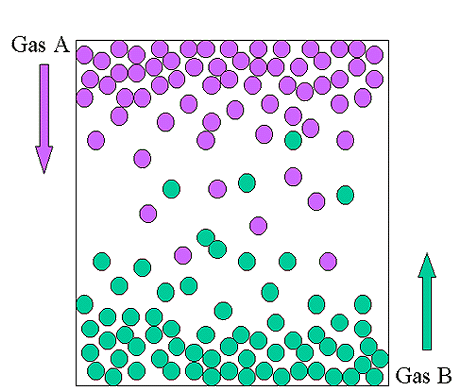
Diffusion Equation Explanation
Why is the diffusion equation the same as the effusion equation, but for a different reason? In simple diffusion, 2 gases move in opposite directions through a medium with the same pressure everywhere. If the pressure in the medium is constant, then the collisions of one gas with the medium are balanced by the collisions of the other gas. The momentum given to the medium by one gas in an average collision is mV, where m is the mass and V is the diffusion velocity (which is different from the average speed of the particles: it's the overall rate of movement of the gas). The number of collisions is proportional to nv, where n is the number of particles and v is their average speed. Since there is no pressure difference,
\[\left(m_{1}V_{1}\right) \left(n_{1}v_{1}\right) = \left(m_{2}V_{2}\right) \left(n_{2}v_{2}\right)\]
When we rearrange, the relative diffusion flux (nV, amount of particles moving times speed of diffusion) of the gases 1 and 2 is
\[\frac{n_{1}V_{1}}{n_{2}V_{2}} = \frac{m_{2}v_{2}}{m_{1}v_{1}}\]
Because v is proportional to m-1/2, this gives us the same result as the effusion equation. However, the reason is different.
Outside Links
Contributors and Attributions
Emily V Eames (City College of San Francisco)

