21.2: The Nature of Electromagnetic Radiation
- Page ID
- 49636
Visible light, gamma rays, x-rays, ultraviolet (black) light, infrared radiation, microwaves, and radio waves are all related. Many of their properties can be explained by a wave theory: periodically varying electric and magnetic fields (electromagnet waves). Figure \(\PageIndex{1}\) indicates the relationship of these fluctuating electric and magnetic fields. It also illustrates the maximum amplitude A0 and the wavelength λ. The intensity of a wave is associated with the square of its amplitude.
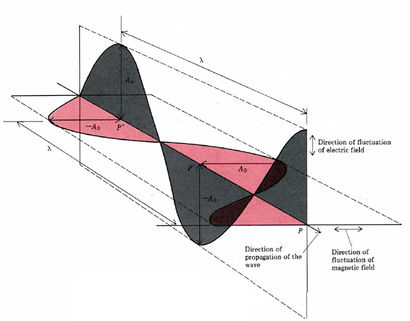
Electromagnetic waves travel through a vacuum at the speed of light, c = 2.9979 × 108 m s–1. The entire wave shown in Figure 21.1 may be thought of as moving from left to right. Thus at position P, where the electric field had maximum amplitude at the instant the figure was drawn there is a progressive decrease in amplitude with time. The amplitude reaches its smallest (most negative) value when the wave has moved a distance equal to that separating points P′ and P. Eventually the amplitude increases to its maximum value again, corresponding to movement of a distance P″ to P, or one wavelength λ. A moving wave can be characterized by the frequency v at which points of maximum amplitude pass a fixed position. The speed of the wave (distance traveled per unit time) must be the product of the wavelength (distance between maxima) and the frequency (number of maxima passing per unit time):
\[ c= \lambda \upsilon \label{1} \]
Since the speed of electromagnetic radiation in a vacuum is always the same, radiation may be characterized by specifying either λ or v. The other quantity can always be calculated from Equation \(\ref{1}\).
Specify the frequency, wavelength, and speed in a vacuum of each of the types of electromagnetic radiation listed below:
- Blue-green light; λ = 500 nm.
- Heat rays emitted from hot asphalt pavement; v = 1.5 × 1014 s–1
- A gamma ray emitted from \( ^{131}_{53} I\) ; λ = 3.402 pm.
- An FM radio transmission; v = 91.5 MHz.
Solution
In each case we make use of the relationship c = λv = 2.998 × 108 m s–1.
- \(v= \frac{c}{ \lambda } = \frac{2.998\times 10^{8}m s{-1}}{500\times10^{-9}m}=6.00\times10^{14}s^{-1}\)
- \(\lambda= \frac{c}{v} = \frac{2.998\times 10^{8}m s{-1}}{1.5\times10^{14}s^{-1}}=2.00\times10^{-6}m=2.0\mu m\)
- \(v= \frac{c}{\lambda} = \frac{2.998\times 10^{8}m s{-1}}{3.402\times10^{-12}m}=8.812\times10^{19}s^{-1}\)
- The unit hertz Hz is 1 s–1, therefore \(\lambda=\frac{2.998\times10^{8}ms^{-1}}{91.5*10^{6}Hz} \times \frac{1 Hz}{1 s^{-1}} = 3.28 m \)
The results obtained in Example \(\PageIndex{1}\) indicate that the frequency and wavelength of electromagnetic radiation can vary over a wide range.
The experiments which did most to convince scientists that light could be described by a wave model are concerned with interference. In 1802 Thomas Young (1773 to 1829), an English physicist, allowed light of a single wavelength to pass through a pair of parallel slits very close to each other and then onto a screen. Young observed the interference pattern of alternating dark and bright strips, shown in Figure \(\PageIndex{2}\). Instead of two strips of light, three appeared on the screen, the most prominent being in the center.
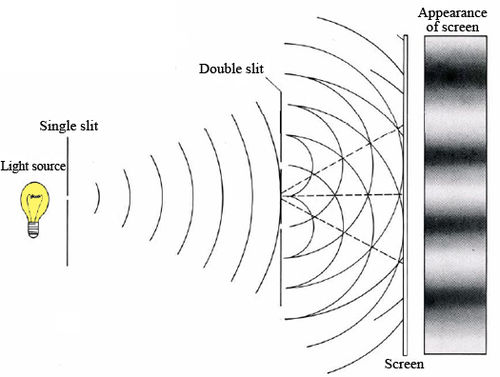
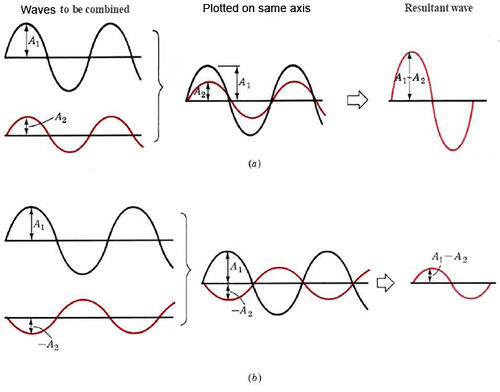
The appearance of these bright and dark strips on the screen is easy to explain if light is regarded as a wave. The bright areas are the result of constructive interference, while the dark ones result from destructive interference. Constructive interference occurs when the crests of two waves reach the same point at the same time. The amplitudes of the two waves add together, giving a resultant larger than either. In the case of destructive interference a maximum in one wave and a minimum in the other reach the same point at the same time. Thus one cancels the effect of the other, and the resultant wave is smaller. This is illustrated in Figure 3. When destructive interference occurs between two waves which have the same amplitude, the resultant wave has zero amplitude (and zero intensity). Hence the dark strips observed in the double-slit experiment.
Although the behavior of light and other forms of electromagnetic radiation can usually be interpreted in terms of wave motion, this is not always so. When radiation is absorbed or emitted by matter, it is usually more convenient to regard it as a stream of particles called photons.
Thus electromagnetic radiation has the same kind of wave-particle duality we encountered in the case of the electron. However, photons have some properties which are very different from those of electrons and other particles. Although photons have mass and energy, and although we can count them, they can travel only at the speed of light. We cannot slow down a photon or stop it without changing it into something else.
The wave-particle duality of photons and electromagnetic radiation is enshrined in an equation first proposed by the German physicist Max Planck (1858 to 1947). The energy of a photon E and the frequency of the electromagnetic radiation associated with it are related in the following way:
\[E=h \upsilon \label{2} \]
where h is a universal constant of nature called Planck’s constant with the value 6.6262 × 10–34 J s. The application of Equation \(\ref{2}\) is best shown by an example.
Calculate the energy of photons associated with each kind of electromagnetic radiation mentioned in Example 1. Compare each result with the mean bond enthalpy for a C—C single bond (348 kJ mol–1).
Solution In each case use the formula E = hv. If wavelengths are given instead of frequencies, the formula E = hc/λ may be obtained by combining Equations \(\ref{1}\) and \(\ref{2}\).
- \(E=\frac{hc}{\lambda}=\frac{6.626\times10^{-34}Js\times2.998\times10^{8}ms^{-1}}{500\times10^{-9}m}=3.97\times10^{-19}J=0.397aJ\)
- \(E=hv=6.626\times10^{-34}Js\times1.5\times10^{14}s^{-1}=9.9\times10^{-20}J=0.099aJ\)
- \(E=\frac{6.626\times10^{-34}Js\times2.998\times10^{8}ms^{-1}}{3.402\times10^{-12}m}=5.839\times10^{-14}J=58 390aJ\)
- \(E=6.626\times10^{-34}Js\times91.5\times10^{-6}s^{-1}=6.06\times10^{-26}J=6.06\times10^{-8}aJ\)
Since the bond enthalpy quoted refers to 1 mol C—C bonds, we must divide by the Avogadro constant to obtain a quantity which is appropriate to compare with the energy of a single quantum of radiation:
Enthalpy to dissociate one C—C bond is
\[\dfrac{348kJmol^{-1}}{6.022\times10^{23}mol^{-1}} = 5.78 \times 10^{–19}\; \,J = 0.578\, aJ \nonumber \]
Clearly the energies of visible photons are comparable with the energies of chemical bonds. Infrared and radio waves have far less energy per photon. Gamma-ray photons have enough energy to break open about 100 000 chemical bonds. As a consequence chemical changes often occur when gamma rays or other high-energy photons are absorbed by matter. Such changes are usually detrimental to living systems, and materials such as lead are used to shield humans from sources of high-energy radiation.
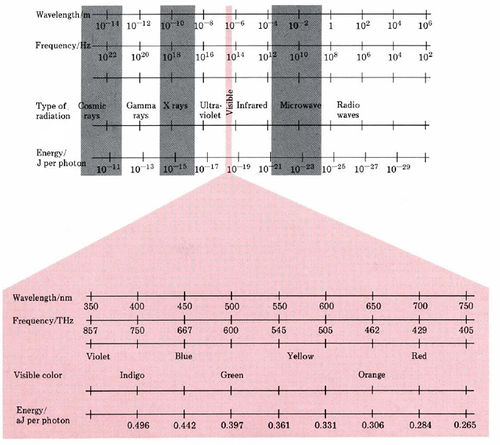
The entire spectrum of electromagnetic radiation may be characterized in terms of wavelength, frequency, or energy per photon, as shown in Figure \(\PageIndex{3}\). The example calculations we have done so far and the figure both indicate the broad range covered by λ, v, and E. Electromagnetic radiation which can be detected by the human retina is but a small slice out of the total available spectrum.