19.9: The Rate of Radioactive Decay
- Page ID
- 49601
We have labeled all isotopes which exhibit radioactivity as unstable, but radioactive isotopes vary considerably in their degree of instability. Some decay so quickly that it is difficult to detect that they are there at all before they have changed into something else. Others have hardly decayed at all since the earth was formed.
The process of radioactive decay is governed by the uncertainty principle, so that we can never say exactly when a particular nucleus is going to disintegrate and emit a particle. We can, however, give the probability that a nucleus will disintegrate in a given time interval. For a large number of nuclei we can predict what fraction will disintegrate during that interval. This fraction will be independent of the amount of isotope but will vary from isotope to isotope depending on its stability. We can also look at the matter from the opposite point of view, i.e., in terms of how long it will take a given fraction of isotope to dissociate. Conventionally the tendency for the nuclei of an isotope to decay is measured by its half-life, symbol t1/2.
This is the time required for exactly half the nuclei to disintegrate. This quantity, too, varies from isotope to isotope but is independent of the amount of isotope.
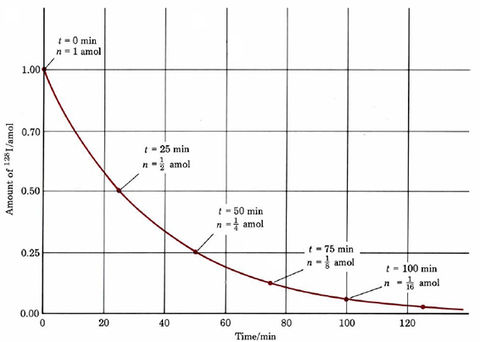
Figure \(\PageIndex{1}\) shows how a 1-amol (attomole) sample of 12853I, which has a half-life of 25.0 min, decays with time. In the first 25 min, half the nuclei disintegrate, leaving behind 0.5 amol. In the second 25 min, the remainder is reduced by one-half again, i.e., to 0.25 amol. After a third 25-min period, the remainder is (½)3 amol, after a fourth it is (½)4 amol, and so on. If x intervals of 25.0 min are allowed to pass, the remaining amount of 12853I will be (½)x amol.
This example enables us to see what will happen in the general case. Suppose the initial amount of an isotope of half-life t1/2 is n0 and the isotope decays to an amount n in time t, we can measure the time in terms of the number of t1/2 intervals which have elapsed by defining a variable x such that
\[x=\frac{t}{t_{\text{1/2}}}\label{1} \]
Thus after time t our sample will have been reduced to a fraction (½)x of the original amount. In other words
\[\frac{n}{n_{\text{0}}}=\left( \frac{\text{1}}{\text{2}} \right)^{x}\label{2} \]
Taking natural logarithm of each side, we then have
\[ln\frac{n}{n_{\text{0}}} = ln \left( \frac{\text{1}}{\text{2}} \right)^{x} = x ln \frac{\text{1}}{\text{2}} = {-{0.693}x}\,\label{3} \]
Substituting from Eq. \(\ref{1}\) we thus obtain
\[ln \frac{n}{n_{\text{0}}} = \frac{-\text{0.693}t}{t_{\text{1/2}}}\label{4} \]
What amount of 12853I will be left when 3.65 amol of this isotope is allowed to decay for 15.0 min. The half-life of 12853I is 25.0 min.
Solution: Substituting in Eq. \(\ref{3}\) we have
\(ln \dfrac{n}{n_{\text{0}}}\) = \(\dfrac{-\text{0}\text{.693}}{t_{\text{1/2}}}\)t = \(\dfrac{-\text{0}\text{.693 }\times \text{ 15}\text{.0 min}}{\text{25}\text{.0 min}}\) = – 0.4158
Thus
\(\dfrac{n}{n_{\text{0}}}\) = e– 0.4158 = 0.6598
or
n = 0.6598n0 = 0.6598 × 3.65 amol = 2.41 amol
Equation \(\ref{2}\) describes how the amount of a radioactive isotope decreases with time, but similar formulas can also be written for the mass m and also for the rate of disintegration r. This is because both the mass and the rate are proportional to the amount of isotope. Thus the rate at which an isotope decays is given by
\[ln\frac{r}{r_{\text{0}}} = \frac{-\text{0}\text{.693}}{t_{\text{1/2}}} \nonumber \]t
where r0 is the initial rate at time zero.
The following example uses equation \(\ref{4}\) to determine the half life of the disintegration of 9038Sr using decay rates taken at two time points.
A sample of 9038Sr has a decay rate of 1.682×106 disintegrations per minute. A year later, the rate of decay has decreased to 1.641×106 disintigrations per minute. What is the half life of 9038Sr?
Solution
We have r0 = 1.682×106 min–1 g–1, while r = 1.641×106 min–1 g–1, and t = 1yr. Substituting into Eq. \(\ref{4}\), we then have
\(ln\dfrac{r}{r_{\text{0}}}\) = \(\dfrac{-\text{0}\text{.693}}{t_{\text{1/2}}}\)t
\(ln\dfrac{1.641 \times 10^6}{1.682 \times 10^6}\) = \(\dfrac{-\text{0}\text{.693}}{t_{\text{1/2}}}\)1 yr
– 0.0247 = \(\dfrac{-\text{0}\text{.693}}{t_{\text{1/2}}}\)1 yr
t1/2 = \(\dfrac{-\text{0}\text{.693}}{-0.0247}\)1 yr=28.1 years
While rates of decay may be used as in example \(\PageIndex{2}\), if masses of either the radioactive substance or the product formed from decay are given, they must first be converted into moles. Then equation \(\ref{3}\) may be used to find any remaining unknown quantities. Example three asks for the age of the sample given masses of the radioactive isotope, product, and half life:
21084Po decays to 20682Pb by emitting an alpha particle. Analysis of a sample originally containing only 21084Po is found to have 0.387 μg of 21084Po and 0.294 μg of 20682Pb. Given a half life of 138 days, how long ago was the original sample produced?
Solution:
Amount of 210Po = nPo = \(\dfrac{\text{0}\text{.387 }\mu \text{g}}{\text{210 g mol}^{-\text{1}}}\) = 1.84 × 10–3 μmol
Amount of 206Pb = nPb = \(\dfrac{\text{0}\text{.294 }\mu \text{g}}{\text{206 g mol}^{-\text{1}}}\) = 1.43 × 10–3 μmol
Since each mol of 206Pb was originally a mole of 210Po, the original amount of 210Po, n0, is given by
n0 = (1.84 + 1.43) × 10–3 μmol = 3.27 × 10–3 μmol
Substituting into Eq. \(\ref{3}\), we have
\(ln\dfrac{n}{n_{\text{0}}}\) = \(\dfrac{-\text{0}\text{.693}}{t_{\text{1/2}}}\)t
\(ln\dfrac{\text{1}\text{.84 }\times \text{ 10}^{-\text{3}}\text{ }\mu \text{mol}}{\text{3}\text{.27 }\times \text{ 10}^{-\text{3}}\text{ }\mu \text{mol}}\) = \(\dfrac{-\text{0}\text{.693}}{138\text{ days}}\) t
– 0.575 = – 5.02 × 10–3 days–1 t
or
t = 115 days


