19.1: Prelude to Nuclear Chemistry
- Page ID
- 50799
In our discussion on Radiation we described the experimental basis for the idea that each atom has a small, very massive nucleus which contains protons and neutrons. Surrounding the nucleus are one or more electrons which occupy most of the volume of the atom but make only a small contribution to its mass. Electrons (especially valence electrons) are the only subatomic particles which are involved in ordinary chemical changes, and we have spent considerable time describing the rearrangements they undergo when atoms and molecules combine. However, another category of reactions is possible in which the structures of atomic nuclei change. In such nuclear reactions electronic structure is incidental—we are primarily interested in how the protons and neutrons are arranged before and after the reaction. Nuclear reactions are involved in transmutation of one element into another and in natural radioactivity. In these sections we consider nuclear reactions in more detail, exploring their applications to nuclear energy, to the study of reaction mechanisms, to qualitative and quantitative analysis, and to estimation of the ages of objects as different as the Dead Sea scrolls and rocks from the moon.
Nuclear reactions involve rearrangements of the protons and neutrons within atomic nuclei. During naturally occurring nuclear reactions α particles, β particles, and γ rays are emitted, often in a radioactive series of successive reactions. Nuclear reactions may also be induced by bombarding nuclei with positive ions or neutrons. Artificial isotopes produced in this way may decay by positron emission or electron capture as well as by α , β or γ emission. Stability of nuclei depends on the neutron/proton ratio (usually between 1 and 1.6) and magic numbers of protons and neutrons.
Radioactive decay obeys a first-order rate law, and its rate is often reported in terms of half-life, the time necessary for half the radioactive nuclei to decompose. Known half-lives of isotopes such as \({}_{\text{6}}^{\text{14}}\text{C}\) and \({}_{\text{92}}^{\text{238}}\text{U}\) may be used to establish the ages of objects containing these elements, provided accurate measurements can be made of the quantity of radiation emitted. Geiger-Müller counters or scintillation counters are often used for such measurements. Other important applications of radioactive isotopes include tracer studies, where a particular type of atom can be labeled and followed throughout a reaction, and neutron activation analysis, which can determine extremely low concentrations of many elements.
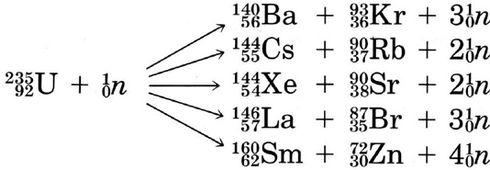
The relative stability of a nucleus is given by the energy of formation per nuclear particle. This may be determined from the difference between the molar mass of the nucleus and the sum of the molar masses of its constituent protons and neutrons. Both fission, breaking apart of a heavy nucleus, and fusion, combining of two light nuclei, can result in release of energy. Fission usually involves \({}_{\text{92}}^{\text{238}}\text{U}\) or , \({}_{\text{94}}^{\text{239}}\text{Pu}\) and these isotopes have been used in nuclear explosives and nuclear power plants. Fission products are highly radioactive. Because of the considerable damage done to living tissue by the ability of α, β and γ radiation to break bonds and form ions, emission of radioactive materials must be carefully controlled and fission power plants are quite expensive to construct. Although it promises much larger quantities of free energy and fewer harmful by-products than fission, nuclear fusion bas not yet been shown to be feasible for use in power plants. So far its only application has been in hydrogen bombs.


