19.14: Nuclear Fission
- Page ID
- 49615
The first time that nuclear fission was achieved in the laboratory was by the Italian physicist Enrico Fermi (1901 to 1954) in 1934. Fermi was among the first to use the neutron in nuclear reactions, following its discovery by Chadwick in 1932. He hoped, by bombarding uranium with slow neutrons, to be able to prepare the first transuranium element. Instead he obtained a product which seemed to be a group II element which he identified incorrectly as radium. It remained for the experienced German radiochemist Otto Hahn to correct Fermi’s mistake. (In the meantime Fermi had been awarded the Nobel Prize.) Somewhat reluctantly, Hahn published a paper early in 1939 showing that the element produced by the bombardment of uranium was not radium at all but the very much lighter group II element barium, 36 places earlier in the periodic table! It then became clear that instead of knocking a small chip off the uranium nucleus as had been expected, the bombarding neutron had broken the nucleus into two large fragments, one of which was barium. We now know that the initial step in this process is the formation of an unstable isotope of uranium which then fissions in a variety of ways, some of which are shown below:
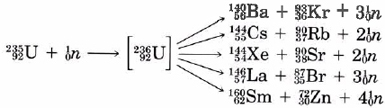
Make a rough estimate of the energy released by the fission of 1 g of uranium-235 according to the equation
\({}_{\text{92}}^{\text{235}}\text{U + }{}_{\text{0}}^{\text{1}}n\text{ }\to \text{ }{}_{\text{56}}^{\text{140}}\text{Ba + }{}_{\text{36}}^{\text{93}}\text{Kr + 3}{}_{\text{0}}^{\text{1}}n\)
using Figure \(\PageIndex{2}\) :
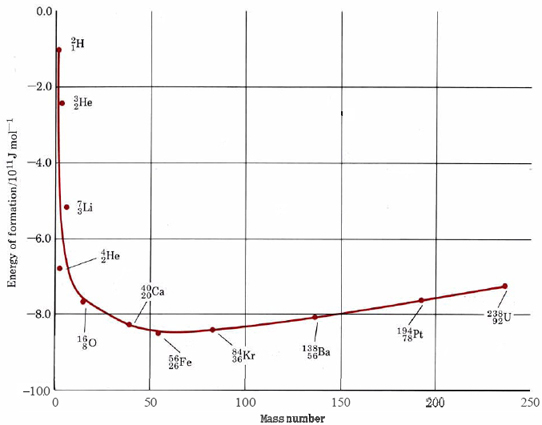
Solution:
From Figure \(\PageIndex{2}\) we can make the following estimates of the energies of formation per nucleon for the four species involved:
-
- ΔHf (140Ba) = – 810 GJ mol–1ΔHf (235U) = – 730 GJ mol–1
-
- ΔHf (93Kr) = – 810 GJ mol–1ΔHf (\({}_{\text{0}}^{\text{1}}n\)) = 0
Using these quantities in the same way as enthalpies of formation for chemical reactions, we obtain
-
- ΔHm = [140(– 810) + 93(– 840) – 235(– 730)] GJ mol–1 = – 20 000 GJ mol–1
The enthalpy change per gram is then given by
-
- ΔH = – 20 000 \(\frac{\text{GJ}}{\text{mol}}\) × \(\frac{\text{1 mol}}{\text{235 g}}\) = – 85 GJ g–1
Note: This is about the same quantity of heat energy as that produced by burning 3 tons of bituminous coal!
Calculations similar to that just performed soon persuaded scientists in 1939 that the fission of uranium was highly exothermic and could possibly be used in a super bomb. Adolph Hitler had been in power in Germany for 6 years, and Europe was teetering on the brink of World War II. The possibility that Nazi Germany might develop such a bomb and use it did not seem remote, especially to those scientists who had recently fled Nazi and Fascist Europe and come to the United States. Albert Einstein, himself one of these refugees, was persuaded to write a letter to President Franklin Roosevelt in August 1939 in which the alarming possibilities were outlined. Roosevelt heeded Einstein’s advice and established the so-called Manhattan Project, a super-secret research effort to develop an atomic bomb if at all possible. After 5 years of intense effort and the expenditure of more money than had ever been spent on a military-scientific project before, the first bomb was tested in New Mexico in July 1945. Shortly thereafter two atom bombs were dropped on the Japanese cities of Hiroshima and Nagasaki, and World War II ended almost immediately.
A crucial feature of the fission of uranium without which an atom bomb is impossible is that fission produces more neutrons than it consumes. As can be seen from Figure \(\PageIndex{2}\), for every neutron captured by a 23592U nucleus, between two and four neutrons are produced. Suppose now that we have a very large sample of the pure isotope 23592U and a stray neutron enters this sample. As soon as it hits a 235U nucleus, fission will take place and about three neutrons will be produced. These in turn will fission three more 235U nuclei, producing a total of nine neutrons. A third repetition will produce 27 neutrons. a fourth 81. and so on. This process (which is called a chain reaction) escalates very rapidly. Within a few microseconds a very large number of nuclei fission, with the release of a tremendous amount of energy, and an atomic explosion results.
There are two reasons why a normal sample of uranium metal does not spontaneously explode in this way. In the first place natural uranium consists mainly of the isotope 23892U while the fissionable isotope 23592U comprises only 0.7 percent of the total. Most of the neutrons produced in a given fission process are captured by 23892U nuclei without any further production of neutrons. The escalation of the fission process thus becomes impossible. However, even a sample of pure 235U will not always explode spontaneously. If it is sufficiently small, many of the neutrons will escape into the surroundings without causing further fission. The sample must exceed a critical mass before an explosion results. In an atomic bomb several pieces of fissionable material, all of which are below the critical mass, are held sufficiently far apart for no chain reaction to occur. When these are suddenly brought together, an atomic explosion results immediately.
A great deal of the 5 years of the Manhattan Project was spent in separating the 0.7 percent of 235U from the more abundant 238U. This was done by preparing the gaseous compound UF6 and allowing it to effuse through a porous screen. (the "Kinetic Theory of Gases" sections discuss that the rate of effusion is inversely proportional to the square root of molar mass.) Each effusion resulted in a gas which was slightly richer in the lighter isotope. Repeating this process eventually produced a compound rich enough in 235U for the purposes of bomb manufacture.
Only the first bomb dropped on Japan used uranium. The second bomb used the artificial element plutonium, produced by the neutron bombardment of 238U:
\[{}_{\text{92}}^{\text{235}}\text{U + }{}_{\text{0}}^{\text{1}}n\text{ }\to \text{ }{}_{\text{94}}^{\text{239}}\text{Pu + 2}{}_{-\text{1}}^{\text{ 0}}e \nonumber \]
Fission of 23984Po occurs in much the same way as for \({}_{\text{92}}^{\text{235}}\text{U}\), giving a variety of products; for example,
\[{}_{\text{94}}^{\text{239}}\text{Pu + }{}_{\text{0}}^{\text{1}}n\text{ }\to \text{ }{}_{\text{38}}^{\text{90}}\text{Sr + }{}_{\text{56}}^{\text{147}}\text{Ba + 3}{}_{\text{0}}^{\text{1}}n \nonumber \]
Again this is a highly exothermic reaction yielding about the same energy per mole (20 000 GJ mol–1) as 235U.


