15.11: Bond Enthalpies and Exothermic or Endothermic Reactions
- Page ID
- 49543
We are in a position to appreciate the general principle which determines whether a gaseous reaction will be exothermic or endothermic. If less energy is needed to break up the reactant molecules into their constituent atoms than is released when these atoms are reconstituted into product molecules, then the reaction will be exothermic. Usually an exothermic reaction corresponds to the breaking of weak bonds (with small bond enthalpies) and the making of strong bonds (with large bond enthalpies). In the hydrogen-fluorine reaction (Figure 1 from Bond Enthalpies) one quite strong bond (DH–H = 436 kJ mol–1) and one very weak bond (DF–F = 159 kJ mol–1) are broken, while two very strong H―F bonds are made. (Note that with a bond enthalpy of 566 kJ mol–1, H―F is the strongest of all single bonds.) The combustion of methane discussed in Example 1 from Bond Enthalpies is another example of the formation of stronger bonds at the expense of weaker ones. The bond enthalpy of the O―H bond is not much different in magnitude from those of the C―H and O=O bonds which it replaces: All lie between 400 and 500 kJ mol–1. The determining factor making this reaction exothermic is the exceedingly large bond enthalpy of the C=O bond which at 803 kJ mol–1 is almost twice as great as for the other bonds involved in the reaction. Not only this reaction but virtually all reactions in which CO2 with its two very strong C=O bonds is produced are exothermic.
In other cases the number of bonds broken or formed can be important. A nice example of this is the highly exothermic (ΔH°(298 K) = –483.7 kJ mol–1) reaction between hydrogen and oxygen to form water:
-
- \[\ce{2H_{2}(g) + O_{2}(g) \rightarrow 2H_{2}O(g)} \nonumber \]
All three types of bonds involved have comparable bond enthalpies:
-
- \(D_{H{-}H} = 436 \text{kJ mol}^{-1}\) \(D_{O{=}O} = 498 \text{kJ mol}^{-1}\) \(D_{O{-}H} = 467 \text{kJ mol}^{-1}\)
but the reason the reaction is exothermic becomes obvious if we rewrite it to make the bonds visible:
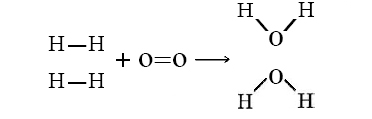
While three bonds must be broken (two H―H and one O=O bond), a total of four bonds are made (four O―H bonds). Since all the bonds are similar in strength, making more bonds than are broken means the release of energy. In mathematical terms
-
- \[\triangle H^{o} = 2D_{H{-}H} + D_{O{=}O} + 4D_{O{-}O} \nonumber \]
-
- \[= 2 * 436 \text{kJ mol}^{-1} + 1 * 498 \text{kJ mol}^{-1} – 4 * 467 \text{kJ mol}^{-1} \nonumber \]
- \[= – 498 \text{kJ mol}^{-1} \nonumber \]
In summary, there are two factors which determine whether a gaseous reaction will be exothermic or not: (1) the relative strengths of the bonds as measured by the bond enthalpies, and (2) the relative number of bonds broken and formed. An exothermic reaction corresponds to the formation of more bonds, stronger bonds, or both.
Since the strength of chemical bonds is a factor in determining whether a reaction will release energy or not, it is obviously important to know which kinds of bonds will be strong and which weak, and we can make some empirical generalizations about the magnitudes of bond enthalpies. The first and most obvious of these is that triple bonds are stronger than double bonds which in turn are stronger than single bonds. As can be seen from Table 1 in Bond Enthalpies, triple bonds have bond enthalpies in the range of 800 to 1000 kJ mol–1. Double bonds range between 400 and 800 kJ mol–1 and single bonds are in the range of 150 to 500 kJ mol–1.
A second generalization is that the strengths of bonds usually increase with polarity. The bond enthalpies of the hydrogen halides, for instance, increase in the order HI < HBr < HCl < HF, and a similar order can be noted for bonds between carbon and halogens. There are exceptions to this rule, though. One would expect the C―N bond to be intermediate in strength between the C―C bond and the C―O bond. As the table shows, it is actually weaker than either.
A third factor affecting the strength of bonds is the size of the atoms. For the most part smaller atoms form stronger bonds. The smallest atom, hydrogen, forms four of the five strongest single bonds in the table. This is not entirely a matter of size since hydrogen is also the most electropositive element featured. Difference in electronegativity, however, does not explain why the H―H bond enthalpy is so large. If we look at the halogens (VIIA elements), we find that the bond enthalpies of I―I, Br―Br, and Cl―Cl increase as expected with decreasing size. The F―F bond is an exception, though: DF―F (158 kJ mol–1) is significantly smaller than DCl―Cl (242 kJ mol–1). Other notable exceptions to this rule are the N―N and O―O bonds. The occurrence of these weak single bonds is of considerable importance to the chemistry of compounds which contain them.The value of a particular bond enthalpy in a given molecule can sometimes be very informative about the nature of the bonding in the molecule. This is especially true of molecules in which resonance is a possibility, as the following example shows.
When benzene is burned in oxygen according to the equation
\[\ce{C_{6}H_{6}(g) + \frac{15}{2} O_{2}(g) \rightarrow 6CO_{2}(g) + 3H_{2}O(g)} \nonumber \] calorimetric measurements give the value of [ΔH°(298 K) as –3169 kJ mol–1 benzene. Use this information together with Table 1 from the Bond Enthalpies section to calculate the mean bond enthalpy for the carbon-carbon bond in benzene.Solution Indicating the required bond enthalpy by the symbol DCC and carefully counting the bonds broken and bonds formed, we have
\[\triangle H^{o} = 6D_{C{-}H} + 6D_{CC} + \frac{15}{2} D_{O{=}O} – C_{C{=}O} + 6D_{O{-}H} \nonumber \] or\[–3169 \text{kJ mol}^{-1} = 6 (416 \text{kJ mol}^{-1}) + 6D_{CC} + \frac{15}{2} (498 \text{kJ mol}^{-1}) – 12 (803 \text{mol}^{-1}) – 6 (467 \text{kJ mol}^{-1}) = –6207 \text{kJ mol}^{-1} + 6D_{CC} \nonumber \]
Thus \[6D_{CC} = (–3169 + 6207) \text{kJ mol}^{-1} = 3038 \text{kJ mol}^{-1} \nonumber \]or \[D_{CC} = 506 \text{kJ mol}^{-1} \nonumber \]
As expected for a resonance structure the bond-enthalpy value is intermediate between that given in the table for a C―C single bond (348 kJ mol–1) and that given for a C=C double bond (614 kJ mol–1).

