10.5: Closest-Packed Structures
- Page ID
- 49659
An important class of crystal structures is found in many metals and also in the solidified noble gases where the atoms (which are all the same) are packed together as closely as possible. Most of us are familiar with the process of packing spheres together, either from playing with marbles or BB’s as children or from trying to stack oranges or other round fruit into a pyramid. On a level surface we can easily arrange a collection of spheres of the same size into a very compact hexagonal layer in which each sphere is touching six of its fellows, as seen in Figure \(\PageIndex{1}\).

Then we can add a second layer so that each added sphere snuggles into a depression between three spheres in the layer below. Within this second layer each sphere also contacts six neighbors, and the layer is identical to the first one. It appears that we can add layer after layer indefinitely, or until we run out of spheres. Each sphere will be touching twelve of its fellows since it is surrounded by six in the same plane and nestles among three in the plane above and three in the plane below. We say that each sphere has a coordination number of 12. It is impossible to make any other structure with a larger coordination number, that is, to pack more spheres within a given volume. Accordingly the structure just described is often referred to as a closest-packed structure. Nickel, shown below, is an example of a metal with a closest-packed structure.

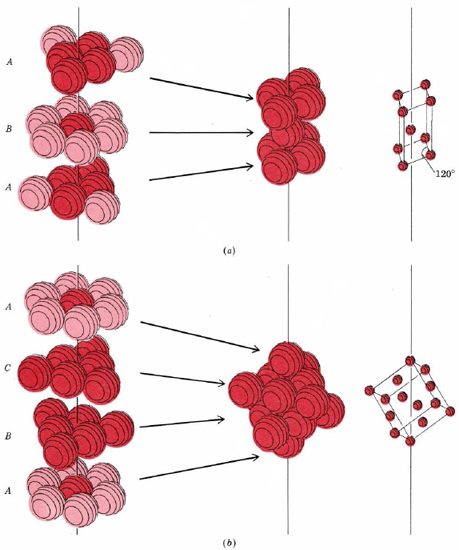
In part a of Figure \(\PageIndex{2}\) the first layer of spheres has been labeled A and the B to indicate that spheres in the second layer are not directly above those in the fist. The third layer is directly above the first, and so it is labeled A. If we continue in the fashion shown, adding alternately A, then B, then A layers, we obtain a structure whose unit cell (shown in part a) has two equal sides with an angle of 120° between them. Other angles are 90°, and so the cell belongs to the hexagonal crystal system. Hence this structure is called hexagonal closest packed (hpc). An example of a metal with an HPC structure is Magnesium, which is shown below.

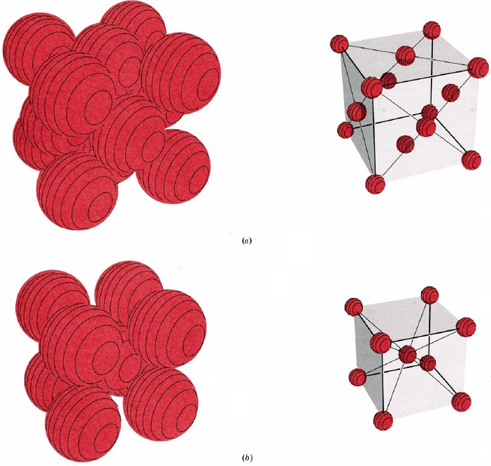
Also shown in Figure \(\PageIndex{3}\) is the unit cell of a structure called body-centered cubic (bcc). This is similar to the fcc structure except that, instead of spheres in the faces, there is a single sphere in the center of the cube. This central sphere is surrounded by eight neighbors at the corners of the unit cell, giving a coordination number of 8. Hence the bcc structure is not as compact as the closest-packed structures which had a coordination number 12. Nevertheless, some metals are found to have bcc structures.
Count the number of spheres in the unit cell of (a) a face-centered cubic structure, and (b) a body-centered cubic structure.
Solution
Referring to the last figure and using the equation:
\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}} \nonumber \]
we find
b) \[N=\text{1 + 0 + 0 + }\frac{\text{8}}{\text{8}}=\text{2} \nonumber \]
Silicon has the same crystal structure as diamond. Techniques are now available for growing crystals of this element which are virtually flawless. Analysis on some of these perfect crystals found the side of the unit cell to be 543.102064 pm long. The unit cell is a cube containing eight Si atoms, but is ont one of the simple cubic cells discussed already. From the isotope make up, molar mass and density of the crystals, it was determined that one mole of Si in this crystal form has a volume of 12.0588349×10-6 m3. Determine NA from this data.
Solution This problem uses knowledge of silicon crystal structure to determine NA. From the edge length, we can obtain the volume of the cubic unit cell. We know that the unit contains eight atoms, and since we know the volume of one mole, we can calculate NA, with the Avogadro constant defined as the number of particles per unit amount of substance.
\[N_{A}= \frac{N*V_{\text{m}}}{V_{\text{unit cell}}}=\frac{8\times{12.0588349}\times{10}^{-6}\text{m}^{3}}{({ 543.102064}\times{10}^{-12}\text{m})^{3}}={6.02214179}\times{10}^{23} \nonumber \]
The values used to determine this value were taken from crystals using X Ray Crystal Density(XRCD), to determine side length. These values were used in the most recent analysis published by the Committee on Data for Science and Technology(CODATA)[1], which standardizes definitions of important scientific constants and units. The value you just calculated is therefore the most accurate determination of Avogadro's constant at this time.
- Mohr, P.J., Taylor, B.N., and D. B. Newell. "CODATA Recommended Values of the Fundamental Physical Constants:fckLR2006." National Institute of Standards and Technology. December 28, 2007. Constants [physics.nist.gov]


