10.10.1: Astronomy- Water on Mars
- Page ID
- 50854
Sunrise Sol gif [chemwiki.ucdavis.edu]
Mars, with an atmosphere of 95.32% CO2 and 0.03% water [2] and temperatures (measured at 1.5 meters above the surface) ranging from + 1° F, ( -17.2° C) to -178° F (-107° C), is not at all Earth-like, but the two planets have a weather phenomenon in common:
A "virga" is a rain or snow shower that evaporates before it reaches the surface, and it appears that virga snowstorms occur on Mars[3]. We can use thermodynamic parameters developed on Earth to understand weather phenomena on Mars, and conditions there are right for snow to evaporate directly into gaseous water (a process called "sublimation"). There are also dry ice storms on Mars that are analogous to thunderstorms on Earth, where the precipitation is solid dry ice.

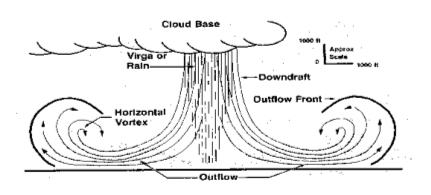
Virgas on Earth can be disastrous to aviation and cause strong damaging winds on the ground because of their heat effects. When a rain virga occurs, the raindrops absorb heat from the air, creating a "microburst" of cold air that descends rapidly, and the heat removed by sublimation of snow showers is much greater.
Although there is some putative evidence for liquid water on Mars, most water exists as ice, mixed in with dry ice (frozen carbon dioxide). Solar radiation may raise equatorial soil temperature to +81°F (27° C) briefly, but the polar cap surface temperatures are always much colder. But even at the highest surface temperatures, most ice appears to sublime. This is because the mean surface level atmospheric pressure is only 600 Pa (0.6 kPa, 0.6% of Earth's 101.3 kPa). The solid carbon dioxide (dry ice) on the surface of Mars sublimes, just as dry ice sublimes on earth.
We can understand these effects in the Earth and Martian atmospheres in terms of the enthalpy of fusion and enthalpy of vaporization of water, described in more familiar terms:
When heat energy is supplied to a solid, like ice, at a steady rate we find that the temperature climbs steadily until the melting point is reached and the first signs of liquid formation become evident. Thereafter, even though we are still supplying heat energy to the system, the temperature remains constant as long as both liquid and solid are present. Only when the last vestiges of the solid have disappeared does the temperature start to climb again.
A large quantity of energy must be supplied to a solid in order to melt it. On a microscopic level melting involves separating molecules which attract each other. This requires an increase in the potential energy of the molecules, and the necessary energy is supplied by the heating coil. The kinetic energy of the molecules (rotation, vibration, and limited translation) remains constant during phase changes, because the temperature does not change.
The heat energy which a solid absorbs when it melts is called the enthalpy of fusion or heat of fusion and is usually quoted on a molar basis. (The word fusion means the same thing as “melting.”) When 1 mol of ice, for example, is melted, we find from experiment that 6.01 kJ are needed. The molar enthalpy of fusion of ice is thus +6.01 kJ mol–1, and we can write
\[\ce{H2O (s) -> H2O (l)} \nonumber \]
(0°C) ΔHm = 6.01 kJ mol–1
If we continue adding heat after the solid melts, the temperature again gradually increases until the liquid begins to boil. At this point, the temperature remains constant until the enthalpy of vaporization has been supplied. Once all the liquid has been converted to vapor, the temperature again rises. In the case of water the molar enthalpy of vaporization is 40.67 kJ mol–1. In other words
\[\ce{H2O (l) -> H2O (g)} \nonumber \]
(100°C) ΔHm = 40.67 kJ mol–1
The enthalpies of fusion and vaporization both depend on temperature and pressure, as you can see in the table of selected molar enthalpies below. Solids like ice which have strong intermolecular forces have much higher values than those like CO2 with weak ones. Even on Earth and Mars, CO2 sublimes rather than melting, then evaporating.
If snow in a virga evaporates at, say 0°C, in removes heat from the surroundings equal to the sum of the heat of fusion and vaporization, which at 0°C is 45.051 + 6.007= 51.058 kJ/mol.[6]
\[\ce{H2O (s) -> H2O (g)} \nonumber \]
(0°C) ΔHsub = 51.058 kJ mol–1 or 2.83 kJ/g
While the temperature of the water does not change during sublimation, the surrounding atmosphere is cooled dramatically. This can be noted as snow on the ground disappears without melting as it sublimes, or as frozen clothes on a clothesline dry without melting.
The enthalpy of sublimation for CO2 at atmospheric pressure, and −78.5 °C (−109.3°F). is
\[\ce{CO2 (s) -> CO2 (g)} \nonumber \]
ΔHsub = 25.2 kJ mol–1 or 0.57 kJ/g. Note that much less heat is required to sublime CO2 (s) than H2O(s).

Table \(\PageIndex{1}\) Molar Enthalpies of Fusion and Vaporization of Selected Substances.
| Substance | Formula | ΔH(fusion) / kJ mol1 |
Melting Point / K | ΔH(vaporization) / kJ mol-1 | Boiling Point / K | (ΔHv/Tb) / JK-1 mol-1 |
|---|---|---|---|---|---|---|
| Neon | Ne | 0.33 | 24 | 1.80 | 27 | 67 |
| Oxygen | O2 | 0.44 | 54 | 6.82 | 90.2 | 76 |
| Methane | CH4 | 0.94 | 90.7 | 8.18 | 112 | 73 |
| Ethane | C2H6 | 2.85 | 90.0 | 14.72 | 184 | 80 |
| Chlorine | Cl2 | 6.40 | 172.2 | 20.41 | 239 | 85 |
| Carbon tetrachloride | CCl4 | 2.67 | 250.0 | 30.00 | 350 | 86 |
| Water* | H2O | 6.00678 at 0°C, 101kPa 6.354 at 81.6 °C, 2.50 MPa |
273.1 | 40.657 at 100 °C, 45.051 at 0 °C, 46.567 at -33 °C |
373.1 | 109 |
| n-Nonane | C9H20 | 19.3 | 353 | 40.5 | 491 | 82 |
| Mercury | Hg | 2.30 | 234 | 58.6 | 630 | 91 |
| Sodium | Na | 2.60 | 371 | 98 | 1158 | 85 |
| Aluminum | Al | 10.9 | 933 | 284 | 2600 | 109 |
| Lead | Pb | 4.77 | 601 | 178 | 2022 | 88 |
*www1.lsbu.ac.uk/water/data.html
Heat energy is absorbed when a liquid boils because molecules which are held together by mutual attraction in the liquid are jostled free of each other as the gas is formed. Such a separation requires energy. In general the energy needed differs from one liquid to another depending on the magnitude of the intermolecular forces. We can thus expect liquids with strong intermolecular forces to have larger enthalpies of vaporization. The list of enthalpies of vaporization given in the table bears this out.
Two other features of the table deserve mention. One is the fact that the enthalpy of vaporization of a substance is always higher than its enthalpy of fusion. When a solid melts, the molecules are not separated from each other to nearly the same extent as when a liquid boils. Second, there is a close correlation between the enthalpy of vaporization and the boiling point measured on the thermodynamic scale of temperature. Periodic trends in boiling point closely follow periodic trends in heat of vaporization. If we divide the one by the other, we find that the result is often in the range of 75 to 90 J K–1 mol–1. To a first approximation therefore the enthalpy of vaporization of a liquid is proportional to the thermodynamic temperature at which the liquid boils. This interesting result is called Trouton’s rule. An equivalent rule does not hold for fusion. The energy required to melt a solid and the temperature at which this occurs depend on the structure of the crystal as well as on the magnitude of the intermolecular forces.
From ChemPRIME: 10.9: Enthalpy of Fusion and Enthalpy of Vaporization
References
- ↑ Image credit: NASA/JPL-Caltech/University of Arizona/Texas A&M University; Phoenix News [www.nasa.gov]
- ↑ en.Wikipedia.org/wiki/Atmosphere_of_Mars#Water
- ↑ en.Wikipedia.org/wiki/Virga#cite_note-2
- ↑ en.Wikipedia.org/wiki/Virga
- ↑ en.Wikipedia.org/wiki/Microburst
- ↑ www1.lsbu.ac.uk/water/data.html
- ↑ en.Wikipedia.org/wiki/Dry_ice


