10.3: Lattices and Unit Cells
- Page ID
- 49657
The regular three-dimensional arrangement of atoms or ions in a crystal is usually described in terms of a space lattice and a unit cell. To see what these two terms mean, let us first consider the two-dimensional patterns shown in Figure \(\PageIndex{1}\). We can think of each of these three structures as a large number of repetitions in two directions of the parallel-sided figure shown immediately below each pattern.
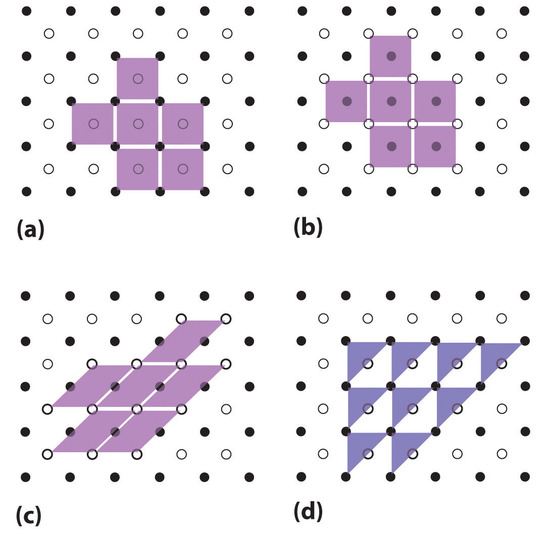
This parallel-sided figure is the unit cell. It represents the simplest, smallest shape from which the overall structure can be constructed. The pattern of points made by the comers of the unit cells when they are packed together is called the space lattice (Figure \(\PageIndex{2}\)). The lines joining the points of the space lattice are shown in color. Without some experience, it is quite easy to pick the wrong unit cell for a given structure. Some incorrect choices are shown immediately below the correct choice in the figure. Note in particular that the unit cell for structure b, in which each circle is surrounded by six others at the comers of a hexagon, is not a hexagon, but a parallelogram of equal sides (a rhombus) with angles of 60 and 120°.
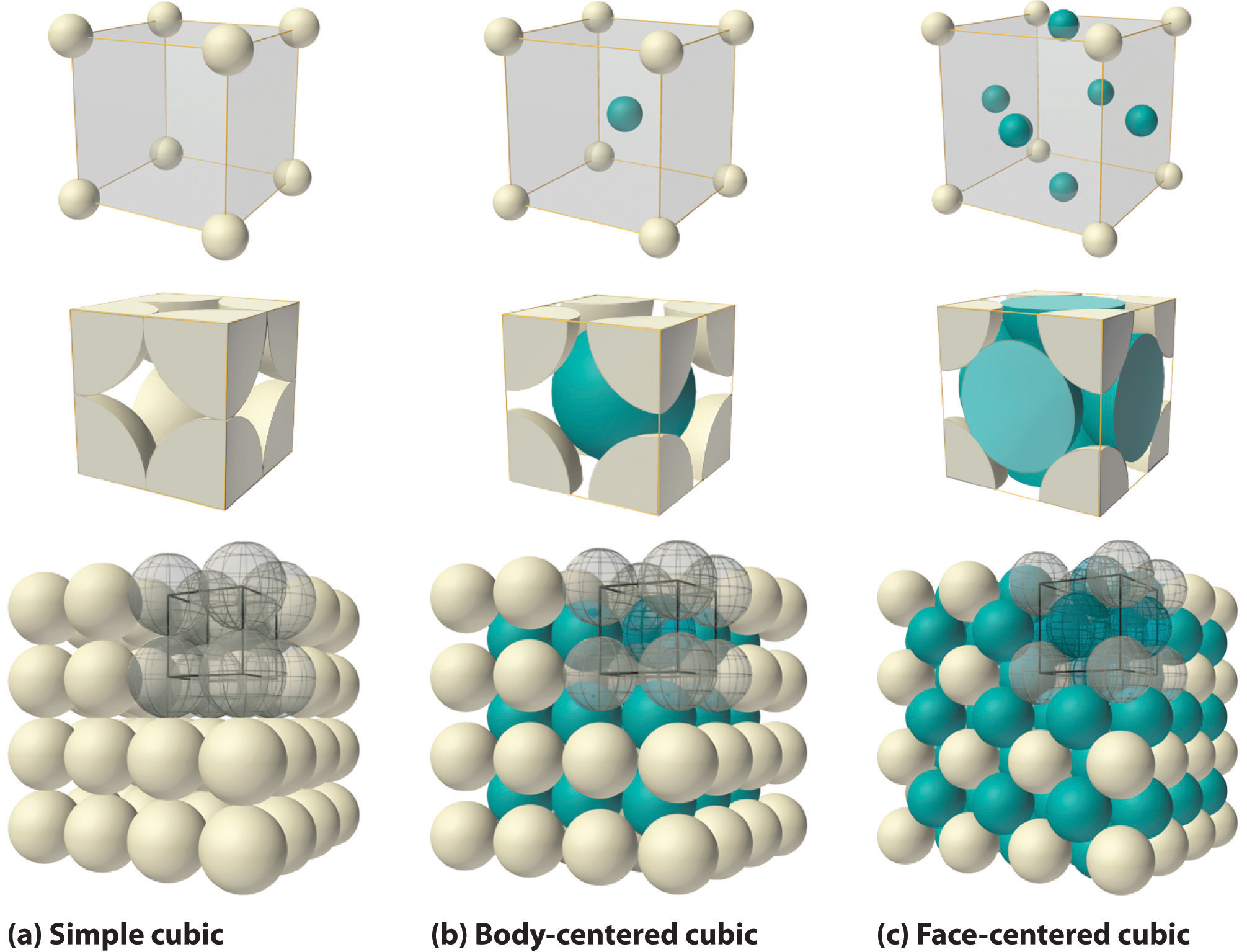
Figure \(\PageIndex{2}\) illustrates the space lattice and the unit cell for a real three-dimensional crystal structure—that of sodium chloride.
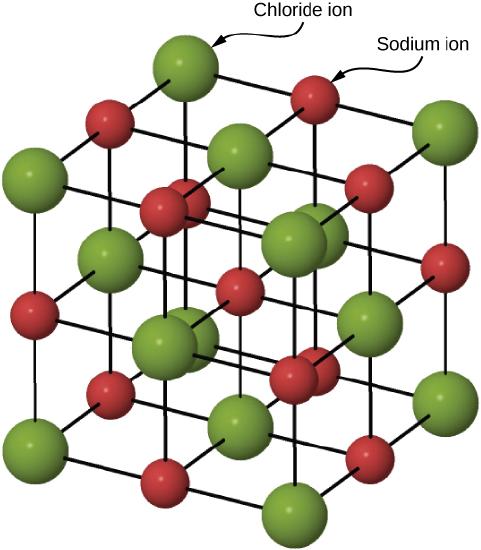

This is the same structure that was shown for lithium hydride, except that the sizes of the ions are different. A unit cell for this structure is a cube whose comers are all occupied by sodium ions. Alternatively, the unit cell could be chosen with chloride ions at the comers.
The unit cell of sodium chloride contains four sodium ions and four chloride ions. In arriving at such an answer we must bear in mind that many of the ions are shared by several adjacent cells (part c of Figure \(\PageIndex{2}\) shows this well). Specifically, the sodium ions at the centers of the square faces of the cell are shared by two cells, so that only half of each lies within the unit cell. Since there are six faces to a cube, this makes a total of three sodium ions. In the middle of each edge of the unit cell is a chloride ion which is shared by four adjacent cells and so counts one-quarter. Since there are twelve edges, this makes three chloride ions. At each comer of the cube, a sodium ion is shared by eight other cells. Since there are eight comers, this totals to one more sodium ion. Finally, there is a chloride ion in the body of the cube unshared by any other cell. The grand total is thus four sodium and four chloride ions.
A general formula can be derived from the arguments just presented for counting N, the number of atoms or ions in a unit cell. It is:
\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}} \nonumber \]


