9.15: Kinetic Theory of Gases- Molecular Speeds
- Page ID
- 49457
Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq. (1) from The Total Molecular Kinetic Energy, we obtain:
\(\begin{align} & PV=nRT=\tfrac{\text{1}}{\text{3}}Nm\text{(}u^{\text{2}}\text{)}_{\text{ave}}\\ & \text{or } \text{3}RT=\frac{Nm}{n}\text{(}u^{\text{2}}\text{)}_{\text{ave}} \label{1}\end{align}\)
Since N is the number of molecules and m is the mass of each molecule, Nm is the total mass of gas. Dividing total mass by amount of substance gives molar mass M: \[M=\frac{Nm}{n} \nonumber \] Substituting in Eq. \(\ref{1}\), we have \(\begin{align} & \text{ 3}RT=M(u^{\text{2}})_{\text{ave}} \\ & \text{or }(u^{\text{2}})_{\text{ave}}=\frac{\text{3}RT}{M} \\ & \text{so that }u_{rms}=\sqrt{\text{(}u^{\text{2}}\text{)}_{\text{ave}}}=\sqrt{\frac{\text{3}RT}{M}}\text{ (2)} \end{align}\) The quantity urms is called the root-mean-square (rms) velocity because it is the square root of the mean square velocity.
The rms velocity is directly proportional to the square root of temperature and inversely proportional to the square root of molar mass. Thus quadrupling the temperature of a given gas doubles the rms velocity of the molecules. Doubling this average velocity doubles the number of collisions between gas molecules and the walls of a container. It also doubles the impulse of each collision. Thus the pressure quadruples. This is indicated graphically in Figure \(\PageIndex{1}\). Pressure is thus directly proportional to temperature, as required by Gay-Lussac’s law.
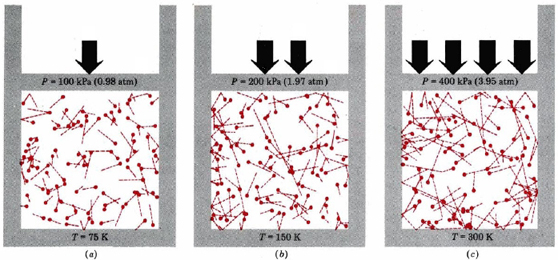
The inverse proportionality between root-mean-square velocity and the square root of molar mass means that the heavier a molecule is, the slower it moves, which is verified by the examples below.
We can compare the rates of effusion or diffusion of a known gas with that of an unknown gas to determine the molar mass of the unknown gas. A convenient equation can be derived easily by considering the kinetic energy of individual molecules rather than moles of gas:
Knowing that kinetic energy is proportional to temperature, if the two gases are at the same temperature,
-
- \(\text{K} \text{E}_{1} = \text{K} \text{E}_{2} \) where 1 and 2 denote the two gases. Since \(KE= \frac{1}{2} m v^{2}\),
- \( \frac{1}{2} m_{1} ( u_{\text{rms, 1}} )^{2} = \frac{1}{2} m_{2} ( u_{\text{rms, 2}} )^{2}\) where m is the atomic weight in amu/average molecule, and urms is the velocity.
Dividing,
\[\frac{m_{1}}{m_{2}} = \frac{ ( u_{rms,2} )^{2} }{u_{rms,1} )^{2} } \nonumber \]
What is the molar mass of an unknown gas if the gas effuses through a pinhole into a vacuum at a rate of 2 mL/min, and H2 effuses at 11 mL/min. Assume that the rate of effusion is proportional to the gas molecule velocities.
Solution
\[\frac{m_{1}}{m_{2}} = \frac{ ( u_{rms,2} )^{2} }{u_{rms,1} )^{2} } \\ \frac{4}{m_{2}} = \frac{2^{2}}{11^{2}} \\ m_{2} = 121 \nonumber \]
Find the rms velocity for (a) H2 and (b) O2 molecules at 27°C.
Solution This problem is much easier to solve if we use SI units. Thus we choose:
R = 8.314 J mol–1 K–1 = 8.314 kg m2s–2 mol–1 K–1
a) For H2 \(\begin{align}u_{\text{rms}}=\sqrt{\frac{\text{3}RT}{M}} & =\sqrt{\frac{\text{3 }\times \text{ 8}\text{.314 J mol}^{-\text{1}}\text{ K}^{-\text{1}}\text{ }\times \text{ 300 K}}{\text{2}\text{.016 g mol}^{-\text{1}}}}\\ & =\sqrt{\text{3}\text{.712 }\times \text{ 10}^{\text{3}}\text{ }\frac{\text{kg m}^{\text{2}}\text{s}^{-\text{2}}}{\text{g}}}\\ & =\sqrt{\text{3}\text{.712 }\times \text{ 10}^{\text{3}}\text{ }\times \text{ 10}^{\text{3}}\text{ }\frac{\text{g m}^{\text{2}}\text{s}^{-\text{2}}}{\text{g}}}\\ & =\sqrt{\text{3}\text{.712 }}\times \text{ 10}^{\text{3}}\text{ m s}^{-\text{1}}=\text{1}\text{.927 }\times \text{ 10}^{\text{3}}\text{ m s}^{-\text{1}}\end{align}\) b) For O2 \[u_{\text{rms}}=\sqrt{\frac{\text{3 }\times \text{ 8}\text{.314 J mol}^{-\text{1}}\text{ K}^{-\text{1}}\text{ }\times \text{ 300 K}}{\text{32}\text{.00 g mol}^{-\text{1}}}}=\text{4}\text{.836 }\times \text{ 10}^{\text{2}}\text{ m s}^{-\text{1}} \nonumber \]The rms velocities 1927 m s–1 and 484 m s–1 correspond to about 4300 miles per hour and 1080 miles per hour, respectively. The O2 molecules in air at room temperature move about 50 percent faster than jet planes, and H2 molecules are nearly 4 times speedier yet. Of course an O2 molecule would take a lot longer to get from New York to Chicago than a jet would. Gas molecules never go far in a straight line before colliding with other molecules.
Now we can see the microscopic basis for Avogadro’s law. Most of the volume in H2, O2 or any gas is empty space, and that empty space is the same for a given amount of any gas at the same temperature and pressure. This happens because the total kinetic energy of the molecules is the same for H2 or O2 or any other gas. The more energy they have, the more room the molecules can make for themselves by expanding against a constant pressure. This is illustrated in Figure \(\PageIndex{2}\), where equal numbers of H2 and O2 molecules occupy separate containers at the same temperature and pressure.
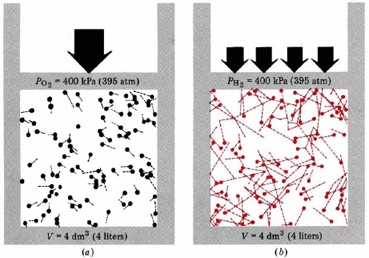
The volumes are seen to be the same. Because O2 molecules are 16 times heavier than H2 molecules, the average speed of H2 molecules is 4 times faster. H2 molecules therefore make 4 times as many collisions with walls. Based on mass, each collision of an H2 molecule with the wall has one-sixteenth the effect of an O2 collision, but an H2 collision has 4 times the effect of an O2 collision when molecular velocity is considered. The net result is that each H2 collision is only one-fourth as effective as an O2 collision. But since there are four times as many collisions, each one-fourth as effective, the same pressure results. Thus the same number of O2 molecules as H2 molecules is required to occupy the same volume at the same temperature and pressure.


