9.12: Dalton's Law of Partial Pressures
- Page ID
- 49453
The ideal gas law can also be rearranged to show that the pressure of a gas is proportional to the amount of gas:
\[P=\frac{RT}{V}\,n\label{1} \]
Thus the factor RT/V may be used to interconvert amount of substance and pressure in a container of specified volume and temperature.
Equation \(\ref{1}\) is also useful in dealing with the situation where two or more gases are confined in the same container (i.e., the same volume). Suppose, for example, that we had 0.010 mol of a gas in a 250-ml container at a temperature of 32°C. The pressure would be
\[\begin{align}P & =\frac{RT}{V}\,n =\frac{\text{0}\text{.0820 liter atm mol}^{-\text{1}}\text{ K}^{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 liter}}\,\times \text{ 0}\text{.010 mol}\\ & =\text{1}\text{.00 atm}\end{align} \nonumber \]
Now suppose we filled the same container with 0.004 mol H2(g) at the same temperature. The pressure would be:
\[\begin{align}p_{\text{H}_{\text{2}}} & =\frac{\text{0}\text{.0820 liter atm mol}^{-\text{1}}\text{ K}^{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 liter}}\,\times \text{ 0}\text{.004 mol}\\ & =\text{0}\text{.40 atm}\end{align} \nonumber \]
If we put 0.006 mol N2 in the container,
\[p_{\text{N}_{\text{2}}}=\frac{\text{0}\text{.0820 liter atm mol}^{-\text{1}}\text{ K}^{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 liter}}\,\times \text{ 0}\text{.006 mol}=\text{0}\text{.60 atm} \nonumber \]
Now suppose we put both the 0.004 mol H2 and the 0.006 mol N2 into the same flask together. What would the pressure be? Since the ideal gas law does not depend on which gas we have but only on the amount of any gas, the pressure of the (0.004 + 0.006) mol, or 0.010 mol, would be exactly what we got in our first calculation. But this is just the sum of the pressure that H2 would exert if it occupied the container alone plus the pressure of N2 if it were the only gas present. That is,
\[P_{total} = p_{\text{H}_{2}} + p_{\text{N}_{2}} \nonumber \]
The figure below demonstrates the concept of partial pressure in more concrete terms, showing the pressure of each gas alone in a container and then showing the gases combined pressure once mixed.

We have just worked out an example of Dalton’s law of partial pressures (named for John Dalton, its discoverer). This law states that in a mixture of two or more gases, the total pressure is the sum of the partial pressures of all the components. The partial pressure of a gas is the pressure that gas would exert if it occupied the container by itself. Partial pressure is represented by a lowercase letter p.
Dalton’s law of partial pressures is most commonly encountered when a gas is collected by displacement of water, as shown in Figure 2.
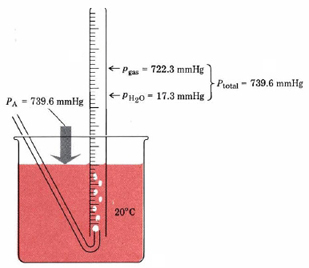
Because the gas has been bubbled through water, it contains some water molecules and is said to be “wet.” The total pressure of this wet gas is the sum of the partial pressure of the gas itself and the partial pressure of the water vapor it contains. The latter partial pressure is called the vapor pressure of water. It depends only on the temperature of the experiment and may be obtained from a handbook or from Table 1.
| Temperature(°C) | Vapor Pressure (mmHg) | Vapor Pressure (kPa) |
|---|---|---|
| 0 | 4.6 | 0.61 |
| 5 | 6.5 | 0.87 |
| 10 | 9.2 | 1.23 |
| 15 | 12.8 | 1.71 |
| 20 | 17.5 | 2.33 |
| 25 | 23.8 | 3.17 |
| 30 | 31.8 | 4.24 |
| 50 | 92.5 | 12.33 |
| 70 | 233.7 | 31.16 |
| 75 | 289.1 | 38.63 |
| 80 | 355.1 | 47.34 |
| 85 | 433.6 | 57.81 |
| 90 | 525.8 | 70.10 |
| 95 | 633.9 | 84.51 |
| 100 | 760.0 | 101.32 |
Assume 0.321 g zinc metal is allowed to react with excess hydrochloric acid (an aqueous solution of HCl gas) according to the equation
\[\text{Zn} (s) + 2 \text{HCL} (aq) \rightarrow \text{Zn} \text{Cl}_{2} (aq) + \text{H}_{2} (g) \nonumber \]
The resulting hydrogen gas is collected over water at 25°C, while the barometric pressure is 745.4 mmHg. What volume of wet hydrogen will be collected?
Solution From Table 1 we find that at 25°C the vapor pressure of water is 23.8 mmHg. Accordingly:
pH2 = ptotal– pH2O = 754 mmHg – 23.8 mmHg = 721.6 mmHg.
This must be converted to units compatible R:
\[p_{\text{H}_{\text{2}}}=\text{721}\text{.6 mmHg }\times \,\frac{\text{1 atm}}{\text{760 mmHg}}=\text{0}\text{.949 atm} \nonumber \]
The road map for this problem is:
\[m_{\text{Zn}}\xrightarrow{M_{\text{Zn}}}n_{\text{Zn}}\xrightarrow{S\left( \text{H}_{\text{2}}\text{/Zn} \right)}n_{\text{H}_{\text{2}}}\xrightarrow{RT/P}V_{\text{H}_{\text{2}}} \nonumber \]
Thus:
\[\begin{align}V_{\text{H}_{\text{2}}} & =\text{0}\text{.321 g Zn }\times \,\frac{\text{1 mol Zn}}{\text{65}\text{.38 g Zn}}\,\times \,\frac{\text{1 mol H}_{\text{2}}}{\text{2 mol Zn}}\,\times \,\frac{\text{0}\text{.0820 liter atm}}{\text{1 K mol H}_{\text{2}}}\,\times \,\frac{\text{293}\text{0.15 K}}{\text{0}\text{.987 atm}}\\ & =\text{0}\text{.126 liter}\end{align} \nonumber \]


