5.4: The Wave Nature of the Electron
- Page ID
- 49286
Historical Development
At much the same time as Lewis was developing his theories of electronic structure, the physicist Niels Bohr was developing a similar, but more detailed, picture of the atom.

Since Bohr was interested in light (energy) emitted by atoms under certain circumstances rather than the valence of elements, he particularly wanted to be able to calculate the energies of the electrons. To do this, he needed to know the exact path followed by each electron as it moved around the nucleus. He assumed paths similar to those of the planets around the sun. The figure seen above illustrates Bohr’s theories applied to the sodium atom. Note how the Bohr model, like that of Lewis, assumes a shell structure. There are two electrons in the innermost shell, eight electrons in the next shell, and a single electron in the outermost shell.
Like Lewis’ model, Bohr’s model was only partially successful. It explained some experimental results but was quite unable to account for others. In particular it failed on the quantitative mathematical level. The Bohr theory worked very well for a hydrogen atom with its single electron, but calculations on atoms with more than one electron always gave the wrong answer. On a chemical level, too, certain features were inadequate. There is no evidence to suggest that atoms of sodium are ever as elongated or as flat as the one in the figure. On the contrary, the way that sodium atoms pack together in a solid suggests that they extend out uniformly in all directions; i.e., they are spherical in shape. Another weakness in the theory was that it had to assume a shell structure rather than explain it. After all, there is nothing in the nature of planets moving around the sun which compels them to orbit in groups of two or eight. Bohr assumed that electrons behave much like planets; so why should they form shells in this way?
One way to explain the fact that electron energies are quantized, or to explain why electrons can be said to exist in particular shells, is to suggest that they behave like standing waves. Ever since Pythagorus' "music of the spheres" we've noted that waves on a string (like a guitar string) produce only certain numerically defined pitches or tones. We can use a wave model to explain why that's so, for a string that is fixed at both ends.
Traveling Waves
If you flick a string, a traveling wave moves down it; if you do this continually, say once a second, you generate a traveling wave train with a frequency of 1 s-1, or one wavelength per second, where the wavelength is the distance between successive peaks (or any other repeating feature) of the wave:
 Image Courtesy of Crash Course Physics
Image Courtesy of Crash Course Physics
There is a relationship between the frequency, usually denoted "ν" ("nu"), the wavelength, usually denoted "λ" (lambda) and the speed that the wave moves down the string (or through space, if it's a light wave). If we denote the speed "c" (a symbol used for the speed of light), the relationship is:
\[\lambda =\dfrac{c}{ u} \label{1} \]
Calculate the wavelength of a microwave in a microwave oven that travels at the speed of light, c = 3.0 x 108 m s-1> and has a wavelength of 2.45 GHz (2.45 x 109 s-1) of 12.24 cm.
Solution
Rearranging \(\ref{1}\) we have:
\[ u =\dfrac{c}{\lambda} \dfrac{\text{3.0}\times \text{10}^{\text{8}}\text{m s}^{\text{-1}}}{\text{2.45}\times\text{10}^{9}\text{s}^{\text{-1}}} = 0.1224\; m = 12.24\, cm \nonumber \]
Microwaves are waves like light waves or radio waves, but their wavelength is much longer than light, and shorter than radio. Waves of this wavelength interact with water molecules make the molecules spin faster and thereby heat up food in a microwave oven.
Standing and Traveling Waves
If the string we're flicking is held on one end and tied at the other end, the waves are reflected backwards, and the backward moving interact with the forward waves to create a constructive interference pattern which appears not to move. It's called a standing wave:
 Standing wave 1
Standing wave 1
 Standing wave 2
Standing wave 2
But some frequencies are not allowed (we do not want the guitar to play all tones at once!). It happens in situations like this:

So the standing wave pattern goes from Standing wave 1 to Standing wave 2, and cannot exist anywhere in between. That's exactly the behavior we find for electrons in shells!. Electrons do not exist anywhere between the shells.
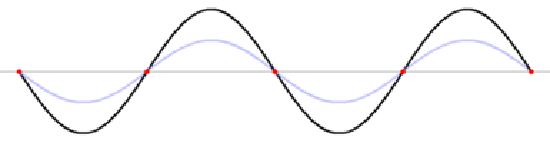
Note that the "nodes" (where there is no motion) don't move, but the "antinodes" vibrate up and down, so the exact position of the string is not fixed. Several more standing waves are shown in the next section; all these have particular frequencies that account for the specific notes produced by a guitar string of particular length, or when the string is "fretted", for example. Videos of another standing wave are shown here.
Light Energy
We usually think of electron shells in terms of their energy. That's because light energy is emitted when an electron falls from a higher shell to a lower one, and measuring light energy is the most important way of determining the energy difference between shells. When electrons change levels, they emit quanta of light called "photons"). The energy of a photon is directly related to its frequency, or inversely related to the wavelength:
\[\text{E} = \text {h} u =\dfrac{\text{h} \text{c}}{\lambda} \label{2} \]
The constant of proportionality h is known as Planck’s constant and has the value 6.626 × 10–34 J s. Light of higher frequency has higher energy and shorter wavelength.
Light can only be absorbed by atoms if each photon has exactly the right amount of energy to promote an electron from a lower shell to a higher one. If more energy is required than a photon possesses, it can't be supplied by bombarding the atom with more photons. So we frequently find that light of one wavelength will cause a photochemical change no matter how dim it is, while light of a neighboring wavelength will not cause a photochemical change no matter how intense it is. That's because photons must be absorbed to cause a photochemical change, and they must have exactly the energy needed to be promoted to the next shell to be absorbed. If they're not absorbed, it doesn't matter how intense the light is (how many photons there are per second).
What wavelength of light is emitted by a hydrogen atom when an electron falls from the third shell, where it has E = -2.42088863 × 10-19J, to the second shell, where it has E = -5.44739997 × 10-19 J?
Solution
ΔE = E2 - E1 = (-5.45 × 10-19) - (-2.42 × 10-19J) = -3.03 × 10-19J.
Note that the energy levels get more negative (more energy is released when an electron falls into them) near the nucleus, and the difference here is negative, meaning energy is released. Taking the absolute value of the energy to calculate the energy of the photon, and rearranging Equation \(\ref{2}\):
\[\lambda =\dfrac{\text{h}\times\text{c}}{E} \nonumber \]
\[λ = \dfrac{(6.626 \times 10^{–34}\; J\; s)(3 \times 10^8)}{3.03 \times 10^{-19}\;J} = 6.56 \times 10^{-7}\; m \nonumber \]
or
\[λ = 656\; nm \nonumber \]
This is the wavelength of red light.
Two Dimensional Standing Waves
Of course the shells for electrons are three dimensional, not one dimensional like guitar strings. We can begin to visualize standing waves in more than one dimension by thinking about wave patterns on a drum skin in two dimensions. Some of the wave patterns are shown below. If you look carefully, you'll see circular nodes that do not move in Modes 2 and 3:

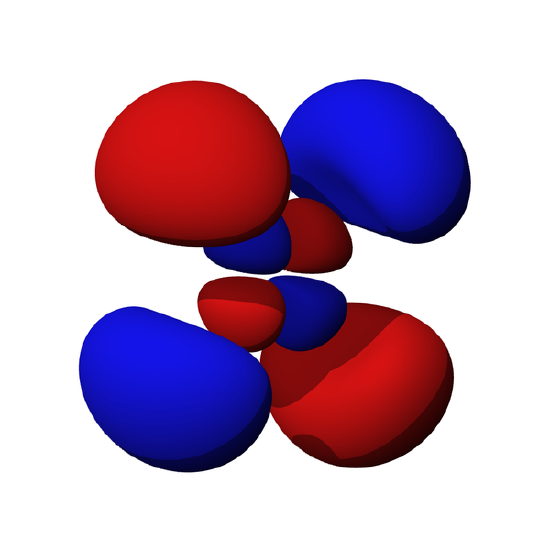
The Shape of Orbitals
Electrons exist around the nucleus in "orbitals", which are three-dimensional standing waves. Electron standing waves are quite beautiful, and we'll see more of them in the next few sections. One example is the flower like "f orbital" below. Here the red parts of the "wavefunction" represent mathematically positive (upward) parts of the standing wave, while blue parts are mathematically negative (downward) parts: