5.7: Electron Waves in the Hydrogen Atom
- Page ID
- 49290
An electron in an atom differs in two ways from the hypothetical electron in a box. First, in an atom the electron occupies all three dimensions of ordinary space. This permits the shapes of the electron waves to be more complicated. Second, the electron is not confined in an atom by the solid walls of a box. Instead, the electrostatic force of attraction between the positive nucleus and the negative electron prevents the latter from escaping.
In 1926 Erwin Schrödinger (1887 to 1961) devised a mathematical procedure by which the electron waves and energies for this more complicated situation could be obtained. A solution of the Schrödinger wave equation is beyond the scope of a general chemistry text. However, a great many chemical phenomena can be better understood if one is familiar with Schrödinger’s results, and we shall consider them in some detail.
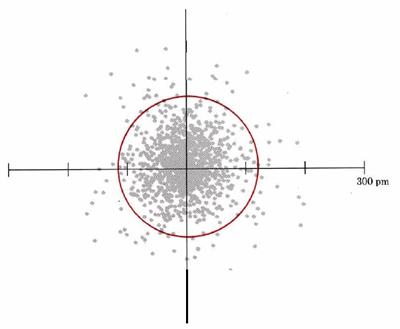
The distribution of electron density predicted by the solution of Schrödinger’s equation for a hydrogen atom which has the minimum possible quantity of energy is illustrated in Figure 1. A number of general characteristics of the behavior of electrons in atoms and molecules may be observed from this figure.
First of all, the hydrogen atom does not have a well-defined boundary. The number of dots per unit area is greatest near the nucleus of the atom at the center of the diagram (where the two axes cross). Electron density decreases as distance from the nucleus increases, but there are a few dots at distances as great as 200 pm (2.00 Å) from the center. Thus as one gets closer and closer to the nucleus of an atom, electron density builds up slowly and steadily from a very small value to a large one. Another way of stating the same thing is to say that the electron cloud becomes more dense as the center of the atom is approached.
A second characteristic evident from Figure 1 is the shape of the electron cloud. In this two-dimensional diagram it appears to be approximately circular; in three dimensions it would be spherical (Figure 2). The following image is a three-dimensional dot-density diagram for the orbital of the hydrogen atom shown in Figure 1. This lowest-energy orbital, called the 1s orbital, appears spherically symmetric. In two dimensions, this can be illustrated more readily by drawing a circle (or in three dimensions, a sphere) which contains a large percentage (say 75 or 90 percent) of the dots, as has been done in the figure above. Since such a sphere or circle encloses most of (but not all) the electron density, it is about as close as one can come to drawing a boundary which encloses the atom. Boundary-surface diagrams in two and three dimensions are easier to draw quickly than are dot-density diagrams. Therefore chemists use them a great deal.