3.10.3: Geology- Calculating the Heat Released by Serpentinization in the "Lost City"
- Page ID
- 50743
Previously, we introduced Serpentinization, the geothermal processes that heat water up to 91°C (196°F) in the geothermal vents in the Atlantic Massif[1]. A "Fly-in video" puts the formation into perspective.
|
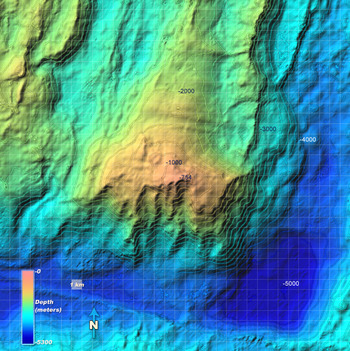
The Atlantis Massif rises ~14,000 feet above the surrounding seafloor and is formed by long-lived faulting[2] |
The actively venting 'IMAX' flange protrudes from the side of the massive Poseidon structure, photographed by the Hercules submersible[3]. |
Calculating the Heat Released by Serpentinization
By now chemists have measured the enthalpy changes for so many reactions that it would take several large volumes to list all the thermochemical equations. Now we'll see how the enthalpy of the serpentinization reaction, and many variations on it that might never get tabulated, can be easily calculated.

For example, if we're interested in one of the main serpentinization reactions which provides heat to the thermal vents:
Forsterite + aqueous silica → serpentine (crysotile)
3 Mg2SiO4(s) + SiO2(aq) + 4 H2O(l) → 2 Mg3Si2O5(s)(OH)4(s) (1)
We can use Hess' law to calculate the ΔHm from a single list of standard enthalpies of formation ΔHf, for all compounds. The standard enthalpy of formation is the enthalpy change when 1 mol of a pure substance is formed from its elements. Each element must be in the physical and chemical form which is most stable at normal atmospheric pressure and a specified temperature (usually 25°C).
For example, if we know that ΔHf[H2O(l)] = –285.8 kJ mol–1, we can immediately write the thermochemical equation
H2(g) + ½O2(g) → H2O(l) ΔHm = –285.8 kJ mol–1 (2) The elements H and O appear as diatomic molecules and in gaseous form because these are their most stable chemical and physical states. Note also that 285.8 kJ are given off per mole of H2O(l) formed. Equation (1) must specify formation of 1 mol H2O(l), and so the coefficient of O2 must be ½.
Example 1
Calculate the Enthalpy change for Equation (1) from the heats of formation of the reactants and products.
| 3 Mg2SiO4 | + SiO2 (aq) | + 4 H2O → | 2 Mg3Si2O5(OH)4 | |
|---|---|---|---|---|
| ΔHf kJ*mol-1* |
-2173.6 | -876.9 | -285.8 | -4360.3 |
*values from SUPCRT[5]
Solution
We can imagine that the reaction takes place in four steps, each of which involves only a standard enthalpy of formation. First, the reactants will be decomposed into their elements, then the elements will be recombined into the product.
In the first step H2O(l) (water) is decomposed to its elements:
4H2O(l) → 2 O2(g) + 4H2(g) ΔH3= (3)
Since this is the reverse of formation of 4 mol H2O(l) from its elements, the enthalpy change is
ΔH3 = 4 mol × {–ΔHf [H2O(l)]} = 4 mol × [– (–285.8 kJ mol–1)] = +1143.2 kJ
In the second step the SiO2(s)similarly decomposes into its elements, with an enthalpy change equal to the negative of its heat of formation:
SiO2(s) → Si(s) + O2(g) ΔH4 (4)
ΔH4 = 1 mol × - ΔHf [SiO2(g)] = 1 mol × -(– 876.9 kJ mol–1) = + 876.9 kJ
The final reactant, 2 Mg2SiO4 decomposes into elements as follows, and the enthalpy change will be twice the negative ΔHm
3 Mg2SiO4 → 6 O2 + 6 Mg (s) + 2 Si(s)ΔH5 (5)
ΔH5 = 3 mol × {–ΔHf [Mg2SiO4]} = 3 mol × [– (–2173.6 kJ mol–1)] = +6520.8 kJ
Finally, we write the reaction for the formation of the product from elements:
6 Mg (s) + 4 Si(s) + 9 O2 + 2 H2O → 2 Mg3Si2O5(OH)4(s) ΔH6 (6)
ΔHm = 2 mol × {ΔHf [Mg3Si2O5(OH)4]} = 2 mol × [(–4360.3 kJ mol–1)] = -8720.6 kJ You can easily verify that the sum of Equations (3)-(6) is Equation (1).
Therefore
ΔHnet = ΔH3 + ΔH4 + ΔH5+ ΔH6
= +1143.2 kJ + 876.9 kJ +6520.8 kJ -8720.6 kJ = – 179.7 kJ mol
Note carefully how Example 1 was solved. The reactant compounds Mg2SiO4(s) SiO2(s) and H2O(l) were hypothetically decomposed to its elements. These equations were the reverse of formation of the compounds, and so ΔH1 was opposite in sign from ΔHf. Step 1 also involved 4 mol H2O(s) and so the enthalpy change had to be multiplied by 4.
In step 2, we had the hypothetical decomposition of SiO2(s), with an enthalpy change which is the negative of ΔHf; finally, the hypothetical decomposition of 3 mol of Mg2SiO4 contributing 3 x -ΔHf, and finally, we had the hypothetical formation of the product Mg3Si2O5(OH)4(s) from its elements. Since 2 mol were obtained, the enthalpy change was doubled but its sign remained the same.
Any chemical reaction can be approached similarly. To calculate ΔHm we add all the ΔHf values for the products, multiplying each by the appropriate coefficient, as in step 2 above. Since the signs of ΔHf for the reactants had to be reversed in step 1, we subtract them, again multiplying by appropriate coefficients. This can he summarized by the equation
ΔHm = ∑ ΔHf (products) – ∑ ΔHf (reactants) (7) The symbol Σ means “the sum of.” Since ΔHf values are given per mole of compound, you must be sure to multiply each ΔHf by an appropriate coefficient derived from the equation for which ΔHm is being calculated.
Applying this equation to the Example we've just completed,
ΔHm = [2 mol x -4360.6 kJ/mol] - [3 mol x 2173.6 kJ/mol) + (1 mol x -876.9 kJ/mol) + (4 mol x -285.8 kJ/mol)] = -179.7 kJ.
This is the enthalpy change for the reaction as written, forming 2 mol of product.
Heats of Formation that Cannot be Measured
In some cases, such as that of water, the elements will react directly to form a compound, and measurement of the heat absorbed serves to determine ΔHf. Quite often, however, elements do not react directly with each other to form the desired compound, and ΔHf must be calculated by combining the enthalpy changes for other reactions. In the case of "aqueous silica", SiO2(aq), the species is not actually formed from Si and O2, yet its enthalpy of formation can be calculated from other known enthalpy changes, and used legitimately as long as the species is specified and well defined.
When silicates dissolve, they form H4SiO4 (silicic acid, sometimes written Si(OH)4). We know the heat of formation of these silica solutions:
- Si(s) + O2(g) + 2 H2(g) + O2(g) → Si(OH)4(qtz) (l) ΔHm = -1457.3 kJ mol–1[6][7] (1)
And we know the enthalpy change for the reaction
- 2 H2O (l) → 2 H2(g) + O2(g) ΔHm = 571.6 kJ mol–1 (2)
So combining the two, and viewing Si(OH)4(aq) as SiO2(aq)•2 H2O, we get a valid heat of formation for :
- Si(s) + O2(g) → SiO2(aq) (l) ΔHm = -885.7 kJ mol–1 (8)
for the fictional species SiO2(aq) (dissolved SiO2 with no Si-O-H bonds), and we can replace SiO2(qtz) + 2 H2O(l) (ΔHf = -910.9 + 571.6 = 1457.3 kJ) with SiO2(aq) (ΔHf = -885.7 kJ) in geothermal equations. In other words, we could have written Equation (1) as
3 Mg2SiO4(s) + Si(OH)4(aq) + 2 H2O(l) → 2 Mg3Si2O5(OH)4{s) ΔHm = -179.7 kJ mol–1[8] (25°C, 1 atm pressure) (1b)
Standard Enthalpy of Formation of Elements
One further point arises from the definition of ΔHf. The standard enthalpy of formation for an element in its most stable state must be zero. If we form oxygen from its elements, for example, we are talking about the reaction
O2(g) → O2(g) Since the oxygen is unchanged, there can be no enthalpy change, and ΔHf = 0 kJ mol–1.
Tables of Standard Enthalpies of Formation
There are many sources of standard enthalpies of formation for geologically important species. A Wikipedia article has references to several of them. Several print compilations are available, including those cited in this exemplar [9]
Many include software that adjusts the values to the high pressures (hundreds of bars (or atmospheres) and temperatures required by geologists. For example, FREED or THERBAL or SUPCRT92[10].
Standard enthalpies of formation for some common compounds are given in the table below. These values may be used to calculate ΔHm for any chemical reaction so long as all the compounds involved appear in the tables. To see how and why this may be done, consider the following example.
Some Standard Enthalpies of Formation at 25°C.
| Compound |
ΔHf/kJ mol–1 |
ΔHf/kcal mol–1 |
Compound |
ΔHf/kJ mol–1 |
ΔHf/kcal mol–1 |
|---|---|---|---|---|---|
| AgCl(s) | –127.068 | –30.35 | H2O(g) | –241.818 | –57.79 |
| AgN3(s) | +620.6 | +148.3 | H2O(l) | –285.8 | –68.3 |
| Ag2O(s) | –31.0 | –7.41 | H2O2(l) | –187.78 | –44.86 |
| Al2O3(s) | –1675.7 | –400.40 | H2S(g) | –20.63 | –4.93 |
| Br2(l) | 0.0 | 0.00 | HgO(s) | –90.83 | –21.70 |
| Br2(g) | +30.907 | +7.385 | I2(s) | 0.0 | 0.0 |
| C(s), graphite | 0.0 | 0.00 | I2(g) | +62.438 | +14.92 |
| C(s), diamond | +1.895 | +0.453 | KCl(s) | –436.747 | –104.36 |
| CH4(g) | –74.81 | –17.88 | KBr(s) | –393.798 | –94.097 |
| CO(g) | –110.525 | –26.41 | MgO(s) | –601.7 | –143.77 |
| CO2(g) | –393.509 | –94.05 | NH3(g) | –46.11 | –11.02 |
| C2H2(g) | +226.73 | +54.18 | NO(g) | +90.25 | +21.57 |
| C2H4(g) | +52.26 | +12.49 | NO2(g) | +33.18 | +7.93 |
| C2H6(g) | –84.68 | –20.23 | N2O4(g) | +9.16 | +2.19 |
| C6H6(l) | +49.03 | +11.72 | NF3(g) | –124.7 | –29.80 |
| CaO(s) | –635.09 | –151.75 | NaBr(s) | –361.062 | –86.28 |
| CaCO3(s) | –1206.92 | –288.39 | NaCl(s) | –411.153 | –98.24 |
| CuO(s) | –157.3 | –37.59 | O3(g) | +142.7 | +34.11 |
| Fe2O3(s) | –824.2 | –196.9 | SO2(g) | –296.83 | –70.93 |
| HBr(g) | –36.4 | –8.70 | SO3(g) | –395.72 | –94.56 |
| HCl(g) | –92.307 | –22.06 | ZnO(s) | –348.28 | –83.22 |
| HI(g) | +26.48 | +6.33 |
Example 2
Use the table of standard enthalpies of formation at 25°C below to calculate ΔHm for the reaction
Forsterite + water → serpentine (chrysotile) + brucite
3 Mg2SiO4(s) +3 H2O(l) → 2 Mg3Si2O5(OH)4(s) + Mg(OH)2(s) ΔHm=? (25°C, 1 atm pressure) (3)
| 3 Mg2SiO4(s) | + 3 H2O(l) → | 2 Mg3Si2O5(OH)4(s) | + Mg(OH)2(s) | |
|---|---|---|---|---|
| ΔHf kJ mol-1 * |
-2173.6 | -285.5 | -4360.3 | -924.20 |
- values from SUPCRT[11]
Solution
Using Eq. (4), we have
ΔHm = ∑ ΔHf (products) – ∑ ΔHf (reactants)
-
- = [1 mol x ΔHf (Mg(OH)2) + 2mol x ΔHf (Mg3Si2O5(OH)4)] – [3 mol x ΔHf (H2O) + 3 mol x ΔHf (Mg2SiO4)]
-
- = 1 mol(–924.20) kJ mol–1 + 2 mol (-4360.3) kJ mol–1 – 3(–285.8 kJ mol–1) – 3 mol × -2173.6 kJ mol–1
-
- = –924.20 kJ -8720.6 kJ + 856.5 kJ + 6520.8 kJ
-
- = -2267 kJ
Reactions like this supply the large amounts of heat necessary to drive the thermal vents of the "Lost City".
Example 3
Use the table of standard enthalpies of formation at 25°C to calculate ΔHm for the reaction
4NH3(g) + 5O2(g) → 6H2O(g) + 4NO(g)
Solution Using Eq. (4), we have
ΔHm = ∑ ΔHf (products) – ∑ ΔHf (reactants)
= [6 ΔHf (H2O) + 4 ΔHf (NO)] – [4 ΔHf (NH3) + 5 ΔHf (O2)]
= 6(–241.8) kJ mol–1 + 4(90.3) kJ mol–1 – 4(–46.1 kJ mol–1) – 5 × 0
= –1450.8 kJ mol–1 + 361.2 kJ mol–1 + 184.4 kJ mol–1
= –905.2 kJ mol–1
Note that we were careful to use ΔHf [H2O(g)] not ΔHf [H2O(l)]. Even though water vapor is not the most stable form of water at 25°C, we can still use its ΔHf value. Also the standard enthalpy of formation of the element O2(g) is zero by definition. Obviously it would be a waste of space to include it in the table above.
References
- ↑ Lost City [en.Wikipedia.org]
- ↑ Geology [www.lostcity.washington.edu]
- ↑ www.lostcity.washington.edu/file/Imax+
- ↑ www.lostcity.washington.edu/f...+Cut+3863-1419
- ↑ GEOPIG Supcrt Application Reactants [geopig3.la.asu.edu:8080]
- ↑ Nordstrom, D.K.; Munoz, J.L. "Geochemical Thermodynamics", 2nd Ed., Blackwell Scientific Publishers, Boston,1994, p. 442
- ↑ Nordstrom, D.K.; Plummer, L.N.; Langmuir, D., et al. "Revised chemical equilibrium data for major water-mineral reactions and their limitations." In Chemical massett, pp. 398-413. American Chemical Society Symposium Series 416.
- ↑ values from SUPCRT. GEOPIG Supcrt Application Reactants [geopig3.la.asu.edu:8080]
- ↑ Robie, R. A.; Hemingway, B.S. "Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 Bar (105 Pascals) Pressure and at Higher Temperatures." U.S. Geological Survey Bulletin 2131, U.S. Government Printing Office, Washington, DC: 1995.
- ↑ GEOPIG Supcrt Application Reactants [geopig3.la.asu.edu:8080]
- ↑ GEOPIG Supcrt Application Reactants [geopig3.la.asu.edu:8080]



