3.9.3: Foods- Fat vs. Sugar Metabolism
- Page ID
- 50741
One of the most useful features of thermochemical equations is that they can be combined to determine ΔHm values for other chemical reactions which have never been observed. We might want to see what ΔHm would be if we could carry out a reaction that has never been done, or it might be interesting for theoretical reasons.
For example, we have noted that the body would have to store up to 67.5 lb of sugar complexes for the energy equivalent of 10 lb of fat.[1]
In Example 1 below, we calculate the energy for the hypothetical reaction in which a fat is converted to sugar:
C18H36O2 (s) + 8 O2(g) → 3 C6H12O6 (s)
ΔHmfor this reaction is the extra energy our body can get from a fat.
A Simple Case
But first, a simpler example may help to make the method clear. Instead of the oxidation of a complicated fat molecule, we'll consider the simplest possible oxidation, a sequence in which carbon itself is oxidized. Step 1 is the oxidation of 1 mol C(s) and 0.5 mol O2(g) to form 1 mol CO(g):
C(s) + ½O2(g) → CO(g) ΔHm = –110.5 kJ = ΔH1 (Note that since the equation refers to moles, not molecules, fractional coefficients are permissible.)
In step 2 the some of the mole of CO reacts with an additional 0.5 mol O2 yielding 1 mol CO2:
CO(g) + ½O2(g) → CO2(g) ΔHm = –283.0 kJ = ΔH2 The net result of this two-step process is production of 1 mol CO2 from the original 1 mol C and 1 mol O2 (0.5 mol in each step). All the CO produced in step 1 is used up in step 2.
On paper this net result can be obtained by adding the two chemical equations as though they were algebraic equations. The CO produced is canceled by the CO consumed since it is both a reactant and a product of the overall reaction
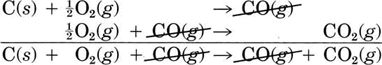 Experimentally it is found that the enthalpy change for the net reaction is the sum of the enthalpy changes for steps 1 and 2: ΔHnet = –110.5 kJ + (–283.0 kJ ) = –393.5 kJ = ΔH1 + ΔH2 That is, the thermochemical equation C(s) + O2(g) → CO2(g) ΔHm = –393.5 kJ is the correct one for the overall reaction.
Experimentally it is found that the enthalpy change for the net reaction is the sum of the enthalpy changes for steps 1 and 2: ΔHnet = –110.5 kJ + (–283.0 kJ ) = –393.5 kJ = ΔH1 + ΔH2 That is, the thermochemical equation C(s) + O2(g) → CO2(g) ΔHm = –393.5 kJ is the correct one for the overall reaction.
Hess' Law
In the general case it is always true that whenever two or more chemical equations can be added algebraically to give a net reaction, their enthalpy changes may also be added to give the enthalpy change of the net reaction.
This principle is known as Hess' law. If it were not true, it would be possible to think up a series of reactions in which energy would be created but which would end up with exactly the same substances we started with. This would contradict the law of conservation of energy. Hess’ law enables us to obtain ΔHm values for reactions which cannot be carried out experimentally, as the next example shows.
Example 1: Fat vs. Sugar Metabolism
EXAMPLE 1
Although fat metabolism is a complicated process (called "beta oxidation") which yields the ATP that releases energy to muscle, we could imagine a reaction that helps us understand why fats store so much energy compared to sugar. We could imagin the combustion of steric acid to the sugar, glucose, according to the equation
(1) C18H36O2 (s) + 8 O2(g) → 3 C6H12O6 (s) ΔHm1
This would represent the "extra" energy that fats provide, over the energy that metabolism of a sugar like glucose provides.
Calculate ΔHm1 for this reaction from the following thermochemical equations, (which are heats of combustion that are easily determined experimentally):
(2) C18H36O2 (s) + 26 O2(g) → 18 CO2(g) + 18 H2O(l) (25°C, 1 atm pressure)
ΔHm2 = –11 407 kJ [2]
(3) C6H12O6 (s) + 6 O2(g) → 6 CO2(g) + 6 H2O(l) (25°C, 1 atm pressure)
ΔHm3 = –2 800 kJ [3]
Solution
We see that reaction (3) has glucose (C6H12O62) on the left, but the target reaction (1) has it on the right. We'll need to reverse equation (3), and then combine it with equation (2) to get the target equation (1). If we reverse (3), we change the sign on ΔHm3:
(3a) 6 CO2(g) + 6 H2O(l)→ C6H12O6 (s) + 6 O2(g) (-) ΔHm3 = +2 800 kJ
But we also might notice that the target equation contains no CO2(g) or H2O(l), so we'll need to multiply equation (3) by 3, so that there will be an equal amount of CO2(g) or H2O(l) on the left and right, and they will cancel. Multiplying equation (3a) by 3:
(3b) 18 CO2(g) + 18 H2O(l)→ 3 C6H12O6 (s) + 18 O2(g) (-3)ΔHm2 = +8 400 kJ
When we combine this equation, and its associated ΔHm with Equation (2), we get the target reaction, (1):
\(\text{C}_{18}\text{H}_{36}\text{O}_{2}\text{(s)} + \text{26 O}_{\text{2}}\text{(g)}\to \)\(\text{18 CO}_{\text{2}}\text{(g)}~+~\text{18 H}_{2}\text{O}~~~~~~~~~~~~~~~~\Delta H_{\text{m}}=\text{11 407 kJ }\)
\( \underline{\text{18 CO}_{\text{2}}\text{(g) + 18 H}_{\text{2}}\text{O}(l)}\underline{\to \text{3 C}_{\text{6}}\text{H}_{\text{12}}\text{O}_{6}\text{(s) +}\text{18 O}_{\text{2}}\text{(g)}}~~~~~~~~\Delta H_{\text{m}}=-3\text{(}-\text{2 800 kJ)}\)
\( \text{C}_{18}\text{H}_{36}\text{O}_{2}\text{(s)} + \text{8 O}_{\text{2}}\text{(g)}\to \text{3 C}_{\text{6}}\text{H}_{\text{12}}\text{O}_{6}\text{(g)} \) \(\Delta H_{\text{m}}=\text{(}\text{-11 407}+\text{8 400 kJ}\text{)}~=~\text{-3007 kJ}\)
ΔHm1 = ΔHm2 + (-3)ΔHm3 = –11 407 + 8400 kJ
ΔHm1 = –3 007 kJ
So one mole (284.48 g) of stearic acid releases 3 007 kJ when it's oxidized to 3 mol of glucose. This is 10.57 kJ/g, or 2.5 Cal/g that we get from fat but not from sugar.
Additionally, for every gram of stearic acid, we get the energy from 1.900 g of glucose (see the stoichiometry summary table below), which provides 4 Cal per gram. This is 1.90 g x 4 Cal/g = 7.59 Cal, so the total energy from 1 g of fat is 2.5 + 7.6 = 10.1 Cal in this case (similar to the 9 Cal/g estimate for typical fats).
| C18H36O2 | + 8 O2 | → 3 C6H12O6 | |
|---|---|---|---|
| m (g) | 1.00 | 0.900 | 1.90 |
| M (g/mol) | 284.4 | 32.0 | 180 |
| n (mol) | 0.00352 | 0.281 | 0.0106 |
References
- Energy from Fats and Sugars
- home.fuse.net/clymer/rq/hoctable.html
- home.fuse.net/clymer/rq/hoctable.html


