15.8: Quantum states, Microstates, and Energy spreading in Reactions
- Page ID
- 96602
You are expected to be able to define and explain the significance of terms identified in bold.
-
energy within a system.
- The entropy of a substance increases with its molecular weight and complexity and with temperature. The entropy also increases as the pressure or concentration becomes smaller. Entropies of gases are much larger than those of condensed phases.
The Physical Meaning of Entropy
Entropy is a measure of the degree of spreading and sharing of thermal energy within a system. This “spreading and sharing” can be spreading of the thermal energy into a larger volume of space or its sharing amongst previously inaccessible microstates of the system. The following table shows how this concept applies to a number of common processes.
| system and process | source of entropy increase of system |
|---|---|
| A deck of cards is shuffled, or 100 coins, initially heads up, are randomly tossed. | This has nothing to do with entropy because macro objects are unable to exchange thermal energy with the surroundings within the time scale of the process |
| Two identical blocks of copper, one at 20°C and the other at 40°C, are placed in contact. | The cooler block contains more unoccupied microstates, so heat flows from the warmer block until equal numbers of microstates are populated in the two blocks. |
| A gas expands isothermally to twice its initial volume. | A constant amount of thermal energy spreads over a larger volume of space |
| 1 mole of water is heated by 1C°. | The increased thermal energy makes additional microstates accessible. (The increase is by a factor of about 1020,000,000,000,000, 000,000,000.) |
| Equal volumes of two gases are allowed to mix. | The effect is the same as allowing each gas to expand to twice its volume; the thermal energy in each is now spread over a larger volume. |
| One mole of dihydrogen, H2, is placed in a container and heated to 3000K. | Some of the H2 dissociates to H because at this temperature there are more thermally accessible microstates in the 2 moles of H. |
| The above reaction mixture is cooled to 300K. | The composition shifts back to virtually all H2because this molecule contains more thermally accessible microstates at low temperatures. |
Entropy is an extensive quantity; that is, it is proportional to the quantity of matter in a system; thus 100 g of metallic copper has twice the entropy of 50 g at the same temperature. This makes sense because the larger piece of copper contains twice as many quantized energy levels able to contain the thermal energy.
Thermal energy is the portion of a molecule's energy that is proportional to its temperature, and thus relates to motion at the molecular scale. What kinds of molecular motions are possible? For monatomic molecules, there is only one: actual movement from one location to another, which we call translation. Since there are three directions in space, all molecules possess three modes of translational motion.
For polyatomic molecules, two additional kinds of motions are possible. One of these is rotation; a linear molecule such as CO2 in which the atoms are all laid out along the x-axis can rotate along the y- and z-axes, while molecules having less symmetry can rotate about all three axes. Thus linear molecules possess two modes of rotational motion, while non-linear ones have three rotational modes. Finally, molecules consisting of two or more atoms can undergo internal vibrations. For freely moving molecules in a gas, the number of vibrational modes or patterns depends on both the number of atoms and the shape of the molecule, and it increases rapidly as the molecule becomes more complicated.
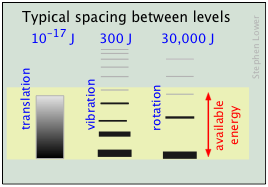
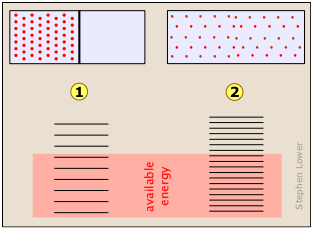
The relative populations of the quantized translational, rotational and vibrational energy states of a typical diatomic molecule are depicted by the thickness of the lines in this schematic (not-to-scale!) diagram. The colored shading indicates the total thermal energy available at an arbitrary temperature. The numbers at the top show order-of-magnitude spacings between adjacent levels.
Notice that the spacing between the quantized translational levels is so minute that they can be considered nearly continuous. This means that at all temperatures, the thermal energy of a collection of molecules resides almost exclusively in translational microstates. At ordinary temperatures (around 25° C), most of the molecules are in their zero-level vibrational and rotational states (corresponding to the bottom-most bars in the diagram.) The prevalence of vibrational states is so overwhelming that we can effectively equate the thermal energy of molecules with translational motions alone.
The number of ways in which thermal energy can be distributed amongst the allowed states within a collection of molecules is easily calculated from simple statistics. A very important point to bear in mind is that the number of discrete microstates that can be populated by an arbitrary quantity of energy depends on the spacing of the states. As a very simple example, suppose that we have two molecules (depicted by the orange dots) in a system total available thermal energy is indicated by the yellow shading.
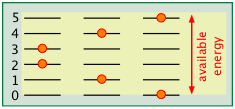
In the system with the more closely-spaced energy levels, there are three possible microstates, while in the one with the more widely-spaced levels, only two possibilities are available.
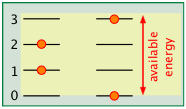
The spacing of molecular energy states becomes closer as the mass and number of bonds in the molecule increases, so we can generally say that the more complex the molecule, the greater the density of its energy states.
At the atomic and molecular level, all energy is quantized; each particle possesses discrete states of kinetic energy and is able to accept thermal energy only in packets whose values correspond to the energies of one or more of these states. Polyatomic molecules can store energy in rotational and vibrational motions, and all molecules (even monatomic ones) will possess translational kinetic energy (thermal energy) at all temperatures above absolute zero. The energy difference between adjacent translational states is so minute that translational kinetic energy can be regarded as continuous (non-quantized) for most practical purposes.
The number of ways in which thermal energy can be distributed amongst the allowed states within a collection of molecules is easily calculated from simple statistics, but we will confine ourselves to an example here. Suppose that we have a system consisting of three molecules and three quanta of energy to share among them. We can give all the kinetic energy to any one molecule, leaving the others with none, we can give two units to one molecule and one unit to another, or we can share out the energy equally and give one unit to each molecule. All told, there are ten possible ways of distributing three units of energy among three identical molecules as shown here:
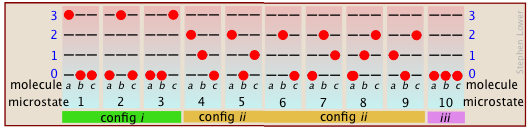
Each of these ten possibilities represents a distinct microstate that will describe the system at any instant in time. Those microstates that possess identical distributions of energy among the accessible quantum levels (and differ only in which particular molecules occupy the levels) are known as configurations. Because all microstates are equally probable, the probability of any one configuration is proportional to the number of microstates that can produce it. Thus in the system shown above, the configuration labeled ii will be observed 60% of the time, while iii will occur only 10% of the time.
As the number of molecules and the number of quanta increases, the number of accessible microstates grows explosively; if 1000 quanta of energy are shared by 1000 molecules, the number of available microstates will be around 10600— a number that greatly exceeds the number of atoms in the observable universe! The number of possible configurations (as defined above) also increases, but in such a way as to greatly reduce the probability of all but the most probable configurations. Thus for a sample of a gas large enough to be observable under normal conditions, only a single configuration (energy distribution amongst the quantum states) need be considered; even the second-most-probable configuration can be neglected.
The bottom line: any collection of molecules large enough in numbers to have chemical significance will have its therrmal energy distributed over an unimaginably large number of microstates. The number of microstates increases exponentially as more energy states ("configurations" as defined above) become accessible owing to
- Addition of energy quanta (higher temperature),
- Increase in the number of molecules (resulting from dissociation, for example).
- the volume of the system increases (which decreases the spacing between energy states, allowing more of them to be populated at a given temperature.)
Using Entropy to Understand Spontaneous Processes
Heat Death
Energy is conserved; if you lift a book off the table, and let it fall, the total amount of energy in the world remains unchanged. All you have done is transferred it from the form in which it was stored within the glucose in your body to your muscles, and then to the book (that is, you did work on the book by moving it up against the earth’s gravitational field). After the book has fallen, this same quantity of energy exists as thermal energy (heat) in the book and table top.
What has changed, however, is the availability of this energy. Once the energy has spread into the huge number of thermal microstates in the warmed objects, the probability of its spontaneously (that is, by chance) becoming un-dispersed is essentially zero. Thus although the energy is still “there”, it is forever beyond utilization or recovery. The profundity of this conclusion was recognized around 1900, when it was first described at the “heat death” of the world. This refers to the fact that every spontaneous process (essentially every change that occurs) is accompanied by the “dilution” of energy. The obvious implication is that all of the molecular-level kinetic energy will be spread out completely, and nothing more will ever happen.
Gases Expansions
Everybody knows that a gas, if left to itself, will tend to expand and fill the volume within which it is confined completely and uniformly. What “drives” this expansion? At the simplest level it is clear that with more space available, random motions of the individual molecules will inevitably disperse them throughout the space. But as we mentioned above, the allowed energy states that molecules can occupy are spaced more closely in a larger volume than in a smaller one. The larger the volume available to the gas, the greater the number of microstates its thermal energy can occupy. Since all such states within the thermally accessible range of energies are equally probable, the expansion of the gas can be viewed as a consequence of the tendency of thermal energy to be spread and shared as widely as possible. Once this has happened, the probability that this sharing of energy will reverse itself (that is, that the gas will spontaneously contract) is so minute as to be unthinkable.
Imagine a gas initially confined to one half of a box (Figure \(\PageIndex{4}\)). The barrier is then removed so that it can expand into the full volume of the container. We know that the entropy of the gas will increase as the thermal energy of its molecules spreads into the enlarged space. In terms of the spreading of thermal energy, Figure \(\PageIndex{5}\) may be helpful. The tendency of a gas to expand is due to the more closely-spaced thermal energy states in the larger volume  .
.
Mixing and dilution
Mixing and dilution really amount to the same thing, especially for idea gases. Replace the pair of containers shown above with one containing two kinds of molecules in the separate sections (Figure \(\PageIndex{6}\)). When we remove the barrier, the "red" and "blue" molecules will each expand into the space of the other. (Recall Dalton's Law that "each gas is a vacuum to the other gas".) However, notice that although each gas underwent an expansion, the overall process amounts to what we call "mixing".
What is true for gaseous molecules can, in principle, apply also to solute molecules dissolved in a solvent. But bear in mind that whereas the enthalpy associated with the expansion of a perfect gas is by definition zero, ΔH's of mixing of two liquids or of dissolving a solute in a solvent have finite values which may limit the miscibility of liquids or the solubility of a solute.
It's unfortunate the the simplified diagrams we are using to illustrate the greater numbers of energetically accessible microstates in an expanded gas or a mixture of gases fail to convey the immensity of this increase. Only by working through the statistical mathematics of these processes (beyond the scope of first-year Chemistry!) can one gain an appreciation of the magnitude of the probabilities of these spontaneous processes.
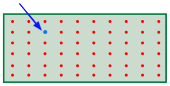
It turns out that when just one molecule of a second gas is inroduced into the container of another gas, an unimaginably huge number of new configurations becom available. This happens because the added molecule (indicated by the blue arrow in the diagram) can in principle replace any one of the old (red) ones, each case giving rise to a new microstate.
Heat Flow
ust as gases spontaneously change their volumes from “smaller-to-larger”, the flow of heat from a warmer body to a cooler one always operates in the direction “warmer-to-cooler” because this allows thermal energy to populate a larger number of energy microstates as new ones are made available by bringing the cooler body into contact with the warmer one; in effect, the thermal energy becomes more “diluted”. In this simplified schematic diagram, the "cold" and "hot" bodies differ in the numbers of translational microstates that are occupied, as indicated by the shading. When they are brought into thermal contact, a hugely greater number of microstates are created, as is indicated by their closer spacing in the rightmost section of the diagram, which represents the combined bodies in thermal equilibrium. The thermal energy in the initial two bodies fills these new microstates to a level (and thus, temperature) that is somewhere between those of the two original bodies.
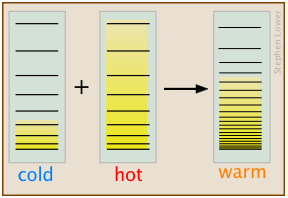
Note that this explanation applies equally well to the case of two solids brought into thermal contact, or two the mixing of two fluids having different temperatures.
As you might expect, the increase in the amount of energy spreading and sharing is proportional to the amount of heat transferred q, but there is one other factor involved, and that is the temperature at which the transfer occurs. When a quantity of heat q passes into a system at temperature T, the degree of dilution of the thermal energy is given by
\[\dfrac{q}{T}\]
To understand why we have to divide by the temperature, consider the effect of very large and very small values of \(T\) in the denominator. If the body receiving the heat is initially at a very low temperature, relatively few thermal energy states are initially occupied, so the amount of energy spreading into vacant states can be very great. Conversely, if the temperature is initially large, more thermal energy is already spread around within it, and absorption of the additional energy will have a relatively small effect on the degree of thermal disorder within the body.
Chemical Reactions and Equilibrium
When a chemical reaction takes place, two kinds of changes relating to thermal energy are involved:
- The ways that thermal energy can be stored within the reactants will generally be different from those for the products. For example, in the reaction H2→ 2 H, the reactant dihydrogen possesses vibrational and rotational energy states, while the atomic hydrogen in the product has translational states only— but the total number of translational states in two moles of H is twice as great as in one mole of H2. Because of their extremely close spacing, translational states are the only ones that really count at ordinary temperatures, so we can say that thermal energy can become twice as diluted (“spread out”) in the product than in the reactant. If this were the only factor to consider, then dissociation of dihydrogen would always be spontaneous and this molecule would not exist.
- In order for this dissociation to occur, however, a quantity of thermal energy (heat) \(q =ΔU\) must be taken up from the surroundings in order to break the H–H bond. In other words, the ground state (the energy at which the manifold of energy states begins) is higher in \(H\), as indicated by the vertical displacement of the right half in each of the four panels below.
In Figure \(\PageIndex{8}\) are schematic representations of the translational energy levels of the two components H and H2 of the hydrogen dissociation reaction. The shading shows how the relative populations of occupied microstates vary with the temperature, causing the equilibrium composition to change in favor of the dissociation product.
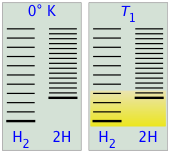
The ability of energy to spread into the product molecules is constrained by the availability of sufficient thermal energy to produce these molecules. This is where the temperature comes in. At absolute zero the situation is very simple; no thermal energy is available to bring about dissociation, so the only component present will be dihydrogen.
- As the temperature increases, the number of populated energy states rises, as indicated by the shading in the diagram. At temperature T1, the number of populated states of H2 is greater than that of 2H, so some of the latter will be present in the equilibrium mixture, but only as the minority component.
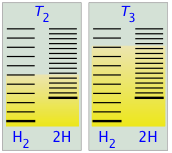
- At some temperature T2 the numbers of populated states in the two components of the reaction system will be identical, so the equilibrium mixture will contain H2 and “2H” in equal amounts; that is, the mole ratio of H2/H will be 1:2.
- As the temperature rises to T3 and above, we see that the number of energy states that are thermally accessible in the product begins to exceed that for the reactant, thus favoring dissociation.
The result is exactly what the Le Chatelier Principle predicts: the equilibrium state for an endothermic reaction is shifted to the right at higher temperatures.
The following table generalizes these relations for the four sign-combinations of ΔH and ΔS. (Note that use of the standard ΔH° and ΔS° values in the example reactions is not strictly correct here, and can yield misleading results when used generally.)
> 0
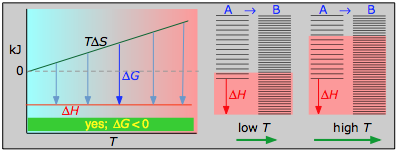
This combustion reaction, like most such reactions, is spontaneous at all temperatures. The positive entropy change is due mainly to the greater mass of CO2 molecules compared to those of O2.
< 0
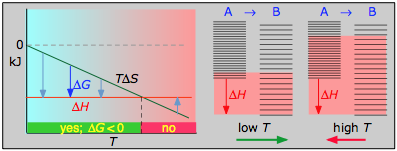
- ΔH° = –46.2 kJ
- ΔS° = –389 J K–1
- ΔG° = –16.4 kJ at 298 K
The decrease in moles of gas in the Haber ammonia synthesis drives the entropy change negative, making the reaction spontaneous only at low temperatures. Thus higher T, which speeds up the reaction, also reduces its extent.
> 0
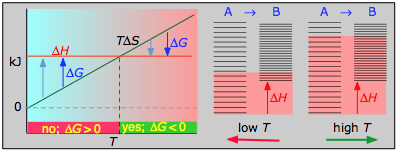
- ΔH° = 55.3 kJ
- ΔS° = +176 J K–1
- ΔG° = +2.8 kJ at 298 K
Dissociation reactions are typically endothermic with positive entropy change, and are therefore spontaneous at high temperatures.Ultimately, all molecules decompose to their atoms at sufficiently high temperatures.
< 0
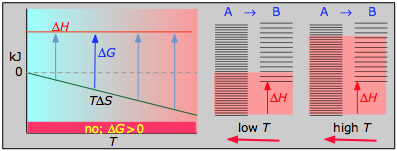
- ΔH° = 33.2 kJ
- ΔS° = –249 J K–1
- ΔG° = +51.3 kJ at 298 K
This reaction is not spontaneous at any temperature, meaning that its reverse is always spontaneous. But because the reverse reaction is kinetically inhibited, NO2 can exist indefinitely at ordinary temperatures even though it is thermodynamically unstable.
Phase Changes
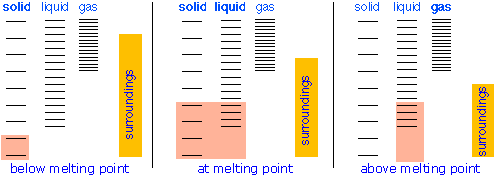
Everybody knows that the solid is the stable form of a substance at low temperatures, while the gaseous state prevails at high temperatures. Why should this be? The diagram in Figure \(\PageIndex{9}\) shows that
- the density of energy states is smallest in the solid and greatest (much, much greater) in the gas, and
- the ground states of the liquid and gas are offset from that of the previous state by the heats of fusion and vaporization, respectively.
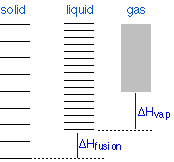
Changes of phase involve exchange of energy with the surroundings (whose energy content relative to the system is indicated (with much exaggeration!) by the height of the yellow vertical bars in Figure \(\PageIndex{13}\). When solid and liquid are in equilibrium (middle section of diagram below), there is sufficient thermal energy (indicated by pink shading) to populate the energy states of both phases. If heat is allowed to flow into the surroundings, it is withdrawn selectively from the more abundantly populated levels of the liquid phase, causing the quantity of this phase to decrease in favor of the solid. The temperature remains constant as the heat of fusion is returned to the system in exact compensation for the heat lost to the surroundings. Finally, after the last trace of liquid has disappeared, the only states remaining are those of the solid. Any further withdrawal of heat results in a temperature drop as the states of the solid become depopulated.
Colligative Properties of Solutions
Vapor pressure lowering, boiling point elevation, freezing point depression and osmosis are well-known phenomena that occur when a non-volatile solute such as sugar or a salt is dissolved in a volatile solvent such as water. All these effects result from “dilution” of the solvent by the added solute, and because of this commonality they are referred to as colligative properties (Lat. co ligare, connected to.) The key role of the solvent concentration is obscured by the greatly-simplified expressions used to calculate the magnitude of these effects, in which only the solute concentration appears. The details of how to carry out these calculations and the many important applications of colligative properties are covered elsewhere. Our purpose here is to offer a more complete explanation of why these phenomena occur.
Basically, these all result from the effect of dilution of the solvent on its entropy, and thus in the increase in the density of energy states of the system in the solution compared to that in the pure liquid. Equilibrium between two phases (liquid-gas for boiling and solid-liquid for freezing) occurs when the energy states in each phase can be populated at equal densities. The temperatures at which this occurs are depicted by the shading.
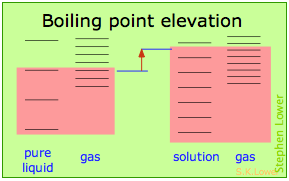
Dilution of the solvent adds new energy states to the liquid, but does not affect the vapor phase. This raises the temperature required to make equal numbers of microstates accessible in the two phases.
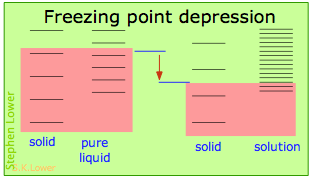
Dilution of the solvent adds new energy states to the liquid, but does not affect the solid phase. This reduces the temperature required to make equal numbers of states accessible in the two phases.
Osmotic Pressure: Effects of Pressure on the Entropy
When a liquid is subjected to hydrostatic pressure— for example, by an inert, non-dissolving gas that occupies the vapor space above the surface, the vapor pressure of the liquid is raised (Figure \(\PageIndex{13}\)). The pressure acts to compress the liquid very slightly, effectively narrowing the potential energy well in which the individual molecules reside and thus increasing their tendency to escape from the liquid phase. (Because liquids are not very compressible, the effect is quite small; a 100-atm applied pressure will raise the vapor pressure of water at 25°C by only about 2 torr.) In terms of the entropy, we can say that the applied pressure reduces the dimensions of the "box" within which the principal translational motions of the molecules are confined within the liquid, thus reducing the density of energy states in the liquid phase.
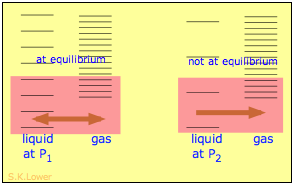
Applying hydrostatic pressure to a liquid increases the spacing of its microstates, so that the number of energetically accessible states in the gas, although unchanged, is relatively greater— thus increasing the tendency of molecules to escape into the vapor phase. In terms of free energy, the higher pressure raises the free energy of the liquid, but does not affect that of the gas phase.
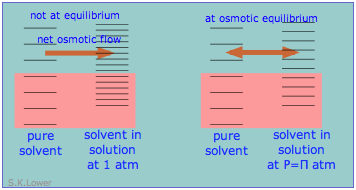
This phenomenon can explain osmotic pressure. Osmotic pressure, students must be reminded, is not what drives osmosis, but is rather the hydrostatic pressure that must be applied to the more concentrated solution (more dilute solvent) in order to stop osmotic flow of solvent into the solution. The effect of this pressure \(\Pi\) is to slightly increase the spacing of solvent energy states on the high-pressure (dilute-solvent) side of the membrane to match that of the pure solvent, restoring osmotic equilibrium.

