15.3: The Second Law of Thermodynamics
- Page ID
- 3600
You are expected to be able to define and explain the significance of terms identified in green type.
- In any macroscopic change, the entropy of the world (that is, system + surroundings) always increases; it never decreases.
- Processes that do not exchange heat with the surroundings (such as the free expansion of a gas into a vacuum) involve entropy change of the system alone, and are always spontaneous.
- A heat engine is a device that converts heat into work. The fraction of heat that can be converted into work is limited by the fall in temperature between the input to the engine and the exhaust.
- According to the Second Law of Thermodynamics, complete conversion of heat into work by a spontaneous cyclic process is impossible.
The First Law of thermodynamics, expressed as ΔU = q + w, is essentially a statement of the law of conservation of energy. The significance of this law is that it tells us that any proposed process that would violate this condition can be dismissed as impossible, without even inquiring further into the details of the process.
Why is the First Law not enough?
For simple mechanical operations on macroscopic objects, the First Law, conservation of energy, is all we usually need to determine such things as how many joules of energy is required to lift a weight or to boil some water, how many grams of glucose you must metabolize in order to climb a hill, or how much fuel your car needs to drive a given distance.
But if you think about it, there are a number of "simple mechanical operations" that never occur, even though they would not violate energy conservation.
- Suppose you drop a book onto a table top. The kinetic energy contained in the falling book is dispersed as thermal energy, slightly warming the book and the table top. According to the First Law, there is no reason why placing pre-warmed book on a warmed table top should not be able to propel the book back into the air. Similarly, why can't the energy imparted to the nail (and to the wood) by a hammer not pop the nail back out?
- One might propose a scheme to propel a ship by means of a machine that takes in seawater, extracts part of its thermal energy which is used to rotate the propeller, and then tosses the resulting ice cubes overboard. As long as the work done to turn the propeller is no greater than the heat required to melt the ice, the First Law is satisfied.
- Because motion of the air molecules is completely random, there is no reason why all of the molecules in one half of a room cannot suddenly "decide" to move into the other half, asphyxiating the unfortunate occupants of that side. (To the extent that air behaves as a perfect gas, this doesn't involve the First Law at all.)
What do all these scenarios that conform to the First Law but are nevertheless never seen to occur have in common? In every case, energy becomes less spread out, less "diluted". In the first two examples, thermal energy (dispersed) gets concentrated into organized kinetic energy of a macroscopic object— a book, a propeller. In the third case, the thermal energy gets concentrated into a smaller volume as the gas contracts.
The second law of thermodynamics says in effect, that the extent to which any natural process can occur is limited by the dilution of thermal energy (increase in entropy) that accompanies it, and once the change has occurred, it can never be un-done without spreading even more energy around. This is one of the most profound laws of nature, and should be a part of every educated person's world view. It is unfortunate that this law is so widely misrepresented as simply ordaining the increase in "disorder". A more brief statement of the Second Law (for those who know the meaning of "entropy") is
Second Law of Thermodynamics: The entropy of the world only increases and never decreases.
The more formal and historical ways of stating the Second Law will be presented farther below after we introduce the topic of heat engines. It is also worth knowing this important consequence of the Second Law: Just because the energy is “there” does not mean it will be available to do anything useful.
Entropy and Spontaneous Change
We explained how processes that take place spontaneously always proceed in a direction that leads to the spreading and sharing of thermal energy.
- A book falls to the tabletop (rather than absorbing heat and jumping up from it) because its kinetic energy changes into thermal energy which is widely dispersed into the molecules of the book and the table.
- A gas expands and solutions mix because the thermal energy their molecules possess get spread over a larger volume of space.
- Hydrogen gas dissociates into H atoms which share thermal energy amongst more particles and a greater volume of space. (But only if the temperature is high enough to make the huge number of new microstates energetically accessible.)
Because all natural processes lead to the spreading and sharing of thermal energy, and because entropy is a measure of the extent to which energy is dispersed in the world, it follows that:
In any spontaneous macroscopic change, the entropy of the world increases.
All natural processes that allow the free exchange of thermal energy amongst chemically-significant numbers of particles are accompanied by a spreading or “dilution” of energy that leaves the world forever changed. In other words, all spontaneous change leads to an increase in the entropy of the world. At first sight, this might seem to be inconsistent with our observations of very common instances in which there is a clear decrease in entropy, such as the freezing of a liquid, the formation of a precipitate, or the growth of an organism.
System + surroundings = the world!
... but it’s the entropy of the system plus surroundings that counts! It is important to understand that the criterion for spontaneous change is the entropy change of the system and the surroundings— that is, of the “world”, which we denote by ΔStotal:
\[ΔS_{total} = ΔS_{system} + ΔS_{surroundings} \label{23.1}\]
The only way the entropy of the surroundings can be affected is by exchange of heat with the system:
\[ΔS_{surroundings} = \dfrac{q_{surr}}{ T} \label{23.2}\]
Thus the freezing of water is accompanied by a flow of heat (the heat of fusion) into the surroundings, causing ΔSsurr to increase. At temperatures below the freezing point, this increase more than offsets the decrease in the entropy of the water itself, so ΔSworld exceeds zero and the process is spontaneous. The problem example below works this out in detail for a specific example.
Note that it does not matter whether the change in the system occurs reversibly or irreversibly; as mentioned previously, it is always possible to define an alternative (irreversible) pathway in which the amount of heat exchanged with the surroundings is the same as qrev ; because ΔS is a state function, the entropy change of the surroundings will have the same value as for the unrealizable reversible pathway.
If there is no flow of heat into or out of the surroundings, the entropy change of the system and that of the world are identical. Examples of such processes, which are always spontaneous, are the free expansion of an ideal gas into a vacuum, and the mixing of two ideal gases. In practice, almost all processes involving mixing and diffusion can be regarded as driven exclusively by the entropy increase of the system.
Most processes involving chemical and phase changes involve the exchange of heat with the surroundings, so their tendency to occur cannot always be predicted by focusing attention on the system alone. Further, owing to the –q/T term in ΔSsurroundings, the spontaneity of all such processes will depend on the temperature, as we illustrated for the dissociation of H2 previously.
As a quantitative example, let us consider the freezing of water. We know that liquid water will spontaneously change into ice when the temperature drops below 0°C at 1 atm pressure. Since the entropy of the solid is less than that of the liquid, we know the entropy of the water (the system here) will decrease on freezing. The amount of decrease is found by dividing the heat of fusion of ice by the temperature for the reversible pathway, which occurs at the normal freezing point:
\[ΔS_{system} = \dfrac{-6000 \; J/mol}{273 \;K} = -21.978 \; J/mol\]
If the process is actually carried at 0°C, then the heat of fusion is transferred to the surroundings at the same temperature, and the entropy of the surroundings increases by
\[ΔS_{surroundings} = \dfrac{6000 \; J/mol}{273 \;K} = 21.979\; J/mol\]
so that ΔStotal = 0. Under these conditions the process can proceed in either direction (freezing or melting) without affecting the entropy of the world; this means that both ice and liquid water can be present simultaneously without any change occurring; the system is said to be in equilibrium.
Suppose now that the water is supercooled to –1°C before it freezes. The entropy change of the water still corresponds to the reversible value qrev/T = (–6000J)/(273K). The entropy change of the surroundings, however, is now given by
\[ΔS_{surroundings} = \dfrac{6000 \; J/mol}{273 \;K} = 22.059\; J/mol\]
The total entropy change is now
\[ΔS_{total} = (–21.978 + 22.059) J;\ K^{–1} mol^{–1} = +0.081\; J \;K^{–1} mol^{–1}\]
indicating that the process can now occur (“is spontaneous”) only in the one direction.
Why did we use 273 K when evaluating ΔSsystem and 272 K for calculating ΔSsurroundings? In the latter case it is possible to formulate a reversible pathway by which heat can be transferred to the surroundings at any temperature. ΔSsystem, however, is a state function of water, and will vary with temperature only slightly.
Note that in order to actually freeze water, it must be cooled to very slightly below its normal freezing point, a condition known as supercooling. Freezing of supercooled water is of course an irreversible process (once it starts, it cannot be stopped except by raising the temperature by a finite amount), and the positive value of \(ΔS_{total}\) tells us that this process will occur spontaneously at temperatures below 273 K. Under these conditions, the process is driven by the entropy increase of the surroundings resulting from flow of the heat of fusion of water into the surroundings.
Does the entropy of the world ever decrease?
The principle that thermal energy (and the molecules carrying it) tends to spread out is based on simple statistics. It must be remembered, however, that the laws of probability have meaningful application only to systems made up of large numbers of independent actors. If you trap a hundred flies in a bottle, they will generally distribute themselves more or less uniformly throughout the container; if there are only four flies, however, it is quite likely that all of them will occasionally be located in one particular half of the bottle.
Why the sky is blue
Similarly, you can trust with complete certainty that the spontaneous movement of half the molecules of the air to one side of the room you now occupy will not occur, even though the molecules are moving randomly and independently. On the other hand, if we consider a box whose dimensions are only a few molecular diameters, then we would expect that the random and short-term displacement of the small number of particles it contains to one side of the box would occur quite frequently. This is, in fact, the cause of the blueness of the sky: random fluctuations in the air density over tiny volumes of space whose dimensions are comparable with the wavelength of light results in selective scattering of the shorter wavelengths, so that blue light is scattered out, leaving the red light for the enjoyment of sunset-watchers to the east.
Brownian motion
This refers to the irregular zig-zag-like movement of extremely small particles such as plant pollen when they are suspended in a drop of liquid. Any such particle is continually being buffeted by the thermal motions of the surrounding liquid molecules. If size of the particle is very large compared to that the the liquid molecules, the forces that result from collisions of these molecules with the particle will cancel out and the particle remains undisturbed. If the particle is very small, however (perhaps only a thousand times larger than a molecule of the liquid), then the chances that it will undergo sufficiently more hits from one direction than from another during a brief interval of time become significant.
In these two examples, the entropy of the system decreases without any compensating flow of heat into the surroundings, leading to a net (but only temporary) decrease in the entropy of the world. This does not represent a failure of the Second Law, however, because no one has ever devised a way to extract useful work from these processes.
Heat Engines
The Industrial Revolution of the 19th century was largely driven by the invention of the steam engine. The first major use of such engines was to pump water out of mines, whose flooding from natural seepage seriously limited the depths to which they could be driven, and thus the availability of the metal ores that were essential to the expansion of industrial activities. The steam engine is a type of heat engine, a device that converts heat, provided by burning a fuel, into mechanical work, typically delivered through the motion of a piston in opposition to an opposing force. An engine is therefore an energy conversion device in which, ideally, every joule of heat released by combustion of the fuel could be extracted as work at the output shaft; such an engine would operate at 100 percent efficiency.
However, engineers of the time were perplexed to find that the efficiencies of steam engines were rather low (usually around 20%), with most of the heat being exhausted uselessly to the environment. Everyone understood that an efficiency exceeding 100% would be impossible (that would violate conservation of energy, and thus the First Law), but it was not clear why efficiencies could not rise significantly beyond the small values observed even as mechanical designs improved

The answer was found by a young French engineer, Sadi Carnot, who in 1824 published an analysis of an idealized heat engine that is generally considered to be the foundation of the science of thermodynamics— notwithstanding the fact that Carnot still accepted the belief that heat is a fluid-like substance called “caloric”. We will not replicate his analysis here (this is normally done in more advanced courses in physical chemistry), but will simply state his conclusion in his own [translated] words:
"The production of motive power is then due in steam-engines not to an actual consumption of caloric, but to its transportation from a warm body to a cold body...the production of heat alone is not sufficient to give birth to the impelling power: it is necessary that there should also be cold; without it, the heat would be useless. The ultimate attainable efficiency of any heat engine will depend on the temperatures at which heat is supplied to and removed from it."
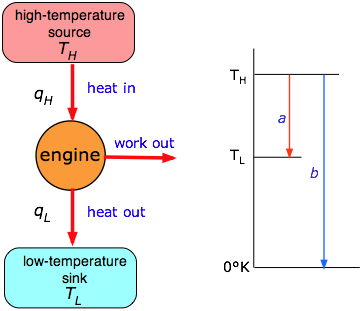
The left side of the figure represents a generalized heat engine into which a quantity of heat qH, extracted from a source or “reservoir” at temperature TH is partly converted into work w. The remainder of the heat qL is exhausted to a reservoir at a lower temperature TL. In practice, TH would be the temperature of the steam in a steam engine, or the temperature of the combustion mixture in an internal combustion or turbine engine. The low temperature reservoir is ordinarily that of the local environment. The efficiency ε (epsilon) of a heat engine is the fraction of the heat abstracted from the high temperature reservoir that can be converted into work:
\[ ε = \dfrac{w}{q_H} \label{3.3}\]
Carnot’s crucial finding (for which he would certainly have deserved a Nobel prize if these had existed at the time) is that the efficiency is proportional to the "distance'' in temperature that the heat can “fall” as it passes through the engine:
\[ ε = 1 - \dfrac{T_L}{T_H} \label{3.4}\]
This is illustrated graphically in the right half of the figure just above, in which the efficiency is simply the fraction of the “complete” fall (in temperature) to absolute zero (arrow b) that the heat undergoes in the engine (arrow a.) Clearly, the only way to attain 100% efficiency would be to set the temperature of the exhaust reservoir to 0°K, which would be impossible. For most terrestrial heat engines, TL is just the temperature of the environment, normally around 300 K, so the only practical way to improve the efficiency is to make TH as high as possible. This is the reason that high pressure (superheated) steam is favored in commercial thermal power plants. The highest temperatures (and the greatest operating efficiencies) are obtained in gas turbine engines. However, as operating temperatures rise, the costs of dealing with higher steam pressures and the ability of materials such as turbine blades to withstand high temperatures become significant factors, placing an upper limit of around 600K on TH, thus imposing a maximum of around 50 percent efficiency on thermal power generation.
For nuclear plants, in which safety considerations require lower steam pressures, the efficiency is lower. One consequence of this is that a larger fraction of the heat is exhausted to the environment, which may result in greater harm to aquatic organisms when the cooling water is returned to a stream or estuary.
Several proposals have been made for building a heat engine that makes use of the temperature differential between the surface waters of the ocean and cooler waters that, being more dense, reside at greater depth. If the exhaust temperature is 5°C, what is the maximum amount of work that could be extracted from 1000 L of surface water at 10°C? (The specific heat capacity of water is 4.184 J g–1K–1.)
Solution
The amount of heat (qH) that must be extracted to cool the water by 5 K is (4.184 J g–1K–1)(106 g)(5 K) = 2.09 × 107 J. The ideal thermodynamic efficiency is given by
\[ 1 -\dfrac{278 \;K}{283\; K} = 0.018\]
The amount of work that could be done would be
\[(0.018)(2.09 \times 10^7 \;J) = 3.7 \times 10^6 \;J\]
Comment: It may be only 1.8% efficient, but it’s free!
The drinking bird as a heat engine
Few toys illustrate as many principles of physical science as this popular device that has been around for many years. At first glance it might appear to be a perpetual motion machine, but it's really just a simple heat engine. Modern "dippy birds" (as they are sometimes called) utilize dichloromethane as the working fluid.

This liquid boils at 39° C, and therefore has a rather high vapor pressure at room temperature. The liquid (to which a dye is often added for dramatic effect) is stored in a reservoir at the bottom of the bird. The bird's beak is covered with felt which, when momentarily dipped in water, creates a cooling effect as the water evaporates. This causes some of the CH2Cl2 vapor to condense in the head, reducing the pressure inside the device, causing more liquid to boil off and re-condense in the head. The redistribution of fluid upsets the balance, causing the bird to dip its beak back into the water. Once the head fills with liquid, it drains back into the bottom, tipping the bird upright to repeat the cycle.
We will leave it to you to relate this to the heat engine diagram above by identifying the heat source and sink, and estimate the thermodynamic efficiency of the engine.
Heat Pumps
If a heat engine is run “in reverse” by performing work on it (that is, changing “work out” to “work in” in Fig 8), it becomes a device for transporting heat against a thermal gradient. Refrigerators and air conditioners are the most commonly-encountered heat pumps. A heat pump can also be used to heat the interior of a building. In this application, the low temperature reservoir can be a heat exchanger buried in the earth or immersed in a well. In this application heat pumps are more efficient than furnaces or electric heating, but the capital cost is rather high.
The Second Law: what it means
It was the above observation by Carnot that eventually led to the formulation of the Second Law of Thermodynamics near the end of the 19th Century. One statement of this law (by Kelvin and Planck) is as follows:
It is impossible for a cyclic process connected to a reservoir at one temperature to produce a positive amount of work in the surroundings.
To help you understand this statement and how it applies to heat engines, consider the schematic heat engine in the figure in which a working fluid (combustion gases or steam) expands against the restraining force of a weight that is mechanically linked to the piston. From a thermodynamic perspective, the working fluid is the system and everything else is surroundings. Expansion of the fluid occurs when it absorbs heat from the surroundings; return of the system to its initial state requires that the surrounding do work on the system. Now re-read the above statement of the Second Law, paying special attention to the italicized phrases which are explained below:
- A cyclic process is one in which the system returns to its initial state. A simple steam engine undergoes an expansion step (the power stroke), followed by a compression (exhaust stroke) in which the piston, and thus the engine, returns to its initial state before the process repeats.
- “At one temperature” means that the expansion and compression steps operate isothermally. This means that ΔU = 0; just enough heat is absorbed by the system to perform the work required to raise the weight, so for this step q = –w.
- “A positive amount of work in the surroundings” means that the engine does more work on the surroundings than the surroundings do on the engine. Without this condition the engine would be useless.
Note carefully that the Second Law applies only to a cyclic process— isothermal expansion of a gas against a non-zero pressure always does work on the surroundings, but an engine must repeat this process continually; to do so it must be returned to its initial state at the end of every cycle. When operating isothermally, the work –w it does on the surroundings in the expansion step (power stroke) is nullified by the work +w the surroundings must do on the system in order to complete the cycle. The Second Law can also be stated in an alternative way:
It is impossible to construct a machine operating in cycles that will convert heat into work without producing any other changes.
Thus the Second Law does allow an engine to convert heat into work, but only if “other changes” (transfer of a portion of the heat directly to the surroundings) are allowed. And since heat can only flow spontaneously from a source at a higher temperature to a sink at a lower temperature, the impossibility of isothermal conversion of heat into work is implied.


