13.3: Finding the pH of weak Acids, Bases, and Salts
- Page ID
- 45384
The numerical examples and the images in this section have some problems (source text with comments).
Make sure you thoroughly understand the following essential concepts that have been presented above.
- Explain the difference between the terms Ca and [HA] as they relate to an aqueous solution of the acid HA.
- Define degree of dissociation and sketch a plot showing how the values of \(alpha\) for a conjugate pair HA and A– relate to each other and to the pKa.
- Derive the relationship between acid concentration and dissociation constant to the hydrogen ion concentration in a solution of a weak acid.
- Re-write the above relation in polynomial form.
- Derive the approximation that is often used to estimate the pH of a solution of a weak acid in water.
- Calculate the pH of a solution of a weak monoprotic weak acid or base, employing the "five-percent rule" to determine if the approximation 2-4 is justified.
- Predict whether an aqueous solution of a salt will be acidic or alkaline, and explain why by writing an appropriate equation.
Most acids are weak; there are hundreds of thousands of them, whereas there are fewer than a dozen strong acids. We can treat weak acid solutions in much the same general way as we did for strong acids. The only difference is that we must now take into account the incomplete "dissociation"of the acid. We will start with the simple case of the pure acid in water, and then go from there to the more general one in which salts of the acid are present. The latter mixtures are known as buffer solutions and are extremely important in chemistry, physiology, industry and in the environment. To keep our notation as simple as possible, we will refer to “hydrogen ions” and [H+] for brevity, and, wherever it is practical to do so, will assume that the acid HA "ionizes" or "dissociates" into H+ and its conjugate base A−.
1 Aqueous solutions of weak acids or bases
A weak acid (represented here as HA) is one in which the reaction
\[HA \rightleftharpoons A^– + H^+ \label{1-1} \]
is incomplete. This means that if we add 1 mole of the pure acid HA to water and make the total volume 1 L, the equilibrium concentration of the conjugate base A– will be smaller (often much smaller) than 1 M/L, while that of undissociated HA will be only slightly less than 1 M/L. Equation \(\ref{1-1}\) tells us that dissociation of a weak acid HA in pure water yields identical concentrations of its conjugate species. Let us represent these concentrations by x. Then, in our "1 M " solution, the concentration of each species is as shown here:
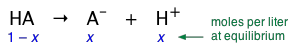 (1-2)
(1-2)
When dealing with problems involving acids or bases, bear in mind that when we speak of "the concentration", we usually mean the nominal or analytical concentration which is commonly denoted by Ca. For example, for a solution made by combining 0.10 mol of pure formic acid HCOOH with sufficient water to make up a volume of 1.0 L, Ca = 0.10 M. However, we know that the concentration of the actual species [HCOOH] will be smaller the 0.10 M because some it ends up as the formate ion HCOO–. It will, of course, always be the case that the sum
\[[HCOOH] + [HCOO^–] = C_a \nonumber \]
For the general case of an acid HA, we can write a mass balance equation
\[C_a = [HA] + [A^–] \label{1-3} \]
which reminds us the "A" part of the acid must always be somewhere!
Similarly, for a base B we can write
\[C_b = [B] + [HB^+] \label{1-4} \]
Equilibrium concentrations of the acid and its conjugate base
According to the above equations, the equilibrium concentrations of A– and H+ will be identical (as long as the acid is not so weak or dilute that we can neglect the small quantity of H+ contributed by the autoprotolysis of H2O). Let us represent these concentrations by x. Then, in a solution containing 1 M/L of a weak acid, the concentration of each species is as shown here:
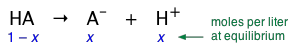 (1-5)
(1-5)
Substituting these values into the equilibrium expression for this reaction, we obtain
\[\dfrac{[A^-][H^+]}{[HA]} = \dfrac{x^2}{1-x} \label{1-6} \]
In order to predict the pH of this solution, we must solve for x. The presence of terms in both x and x 2 here tells us that this is a quadratic equation. In most practical cases in which Ka is 10–4 or smaller, we can assume that x is much smaller than 1 M, allowing us to make the simplifying approximation
\[(1 – x) \approx 1 \label{1-7} \]
so that
\[x^2 \approx K_a \nonumber \]
and thus
\[x = \sqrt{K_a} \label{1-8} \]
This approximation will not generally be valid when the acid is very weak or very dilute.
Solutions of arbitrary concentration
The above development was for a solution made by taking 1 mole of acid and adding sufficient water to make its volume 1.0 L. In such a solution, the nominal concentration of the acid, denoted by Ca, is 1 M.
We can easily generalize this to solutions in which Ca has any value:
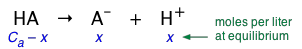 (1-9)
(1-9)
The above relation is known as a "mass balance on A". It expresses the simple fact that the "A" part of the acid must always be somewhere — either attached to the hydrogen, or in the form of the hydrated anion A–.
The corresponding equilibrium expression is
\[\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}=\frac{x^2}{\left(C_a-x\right)}=K_a \label{1-10} \]
and the approximations (when justified) Equation \ref{1-3a} and \ref{1-3b} become
\[(C_a – x) ≈ C_a \label{1-11} \]
\[x ≈ \sqrt{C_a K_a} \label{1-12} \]
Estimate the pH of a 0.20 M solution of acetic acid, Ka = 1.8 × 10–5.
Solution
For brevity, we will represent acetic acid CH3COOH as HAc, and the acetate ion by Ac–. As before, we set x = [H+] = [Ac–], neglecting the tiny quantity of H+ that comes from the dissociation of water.
\[\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right]}{[\mathrm{HAc}]}=\frac{x^2}{(1-x)} \nonumber \]
Substitution into the equilibrium expression yields
\[\frac{x^2}{(0.20-x)}=1.8 \times 10^{-5} \nonumber \]
The rather small value of \(K_a\) suggests that we can drop the \(x\) term in the denominator, so that
\[\dfrac{x^2}{ 0.20} \approx 1.8 \times 10^{-5} \nonumber \]
or
\[x ≈ \sqrt{(0.20)(1.8 \times 10^{–5})} = 1.9 \times 10^{-3}~ M \nonumber \]
The pH of the solution is
\[-\log (1.9 \times 10^{–3}) = 2.7 \nonumber \]
Degree of dissociation
Even though we know that the process HA → H+ + A– does not correctly describe the transfer of a proton to H2O, chemists still find it convenient to use the term "ionization" or "dissociation". The "degree of dissociation" (denoted by \(\alpha\) of a weak acid is just the fraction
\[\alpha = \dfrac{[\ce{A^{-}}]}{C_a} \label{1-13} \]
which is often expressed as a per cent (\(\alpha\) × 100).
Degree of dissociation depends on the concentration
It's important to understand that whereas Ka for a given acid is essentially a constant, \(\alpha\) will depend on the concentration of the acid. Note that these equations are also valid for weak bases if Kb and Cb are used in place of Ka and Ca.
This can be shown by substituting Eq 5 into the expression for Ka:
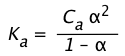 (1-14)
(1-14)
Solving this for \(\alpha\) results in a quadratic equation, but if the acid is sufficiently weak that we can say (1 – ) ≈ 1, the above relation becomes
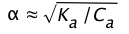 (1-15)
(1-15)
the amount of HA that dissociates varies inversely with the square root of the concentration; as Ca approaches zero, \(\alpha\) approaches unity and [HA] approaches Ca.
This principle is an instance of the Ostwald dilution law which relates the dissociation constant of a weak electrolyte (in this case, a weak acid), its degree of dissociation, and the concentration.
A common, but incorrect explanation of this law in terms of the Le Chatelier principle states that dilution increases the concentration of water in the equation HA + H2O → H3O+ + A–, thereby causing this equilibrium to shift to the right. The error here is that [H2O] in most aqueous solutions is so large (55.5 M) that it can be considered constant; this is the reason the [H2O] term does not appear in the expression for Ka. Another common explanation is that dilution reduces [H3O+] and [A–], thus shifting the dissociation process to the right. However, dilution similarly reduces [HA], which would shift the process to the left. In fact, these two processes compete, but the former has greater effect because two species are involved.
It is probably more satisfactory to avoid Le Chatelier-type arguments altogether, and regard the dilution law as an entropy effect, a consequence of the greater dispersal of thermal energy throughout the system. This energy is carried by the molecular units within the solution; dissociation of each HA unit produces two new particles which then go their own ways, thus spreading (or "diluting") the thermal energy more extensively and massively increasing the number of energetically-equivalent microscopic states, of which entropy is a measure. (More on this here)
Degree of dissociation depends on the pH
Plots of this kind are discussed in more detail in the next lesson in this set under the heading ionization fractions.
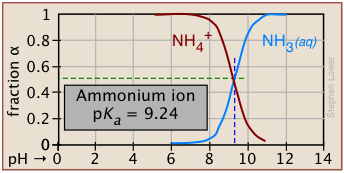
The Le Chatelier principle predicts that the extent of the reaction
\[\ce{HA → H^{+} + A^{–} } \nonumber \]
will be affected by the hydrogen ion concentration, and thus by the pH. This is illustrated here for the ammonium ion. Notice that when the pH is the same as the pKa, the concentrations of the acid- and base forms of the conjugate pair are identical.
A 0.75 M solution of an acid HA has a pH of 1.6. What is its percent dissociation?
Solution
The dissociation stoichiometry HA → H+ + AB– tells us the concentrations [H+] and [A–] will be identical. Thus [H+] = 10–1.6 = 0.025 M = [A–]. The dissociation fraction
\[α = \dfrac{[\ce{A^{–}}]}{[\ce{HA}]} = \dfrac{0.025}{0.75} = 0.033 \nonumber \]
and thus the acid is 3.3% dissociated at 0.75 M concentration.
Sometimes the percent dissociation is given, and Ka must be evaluated.
A weak acid HA is 2 percent dissociated in a 1.00 M solution. Find the value of Ka.
Solution
The equilibrium concentration of HA will be 2% smaller than its nominal concentration, so [HA] = 0.98 M, [A–] = [H+] = 0.02 M. Substituting these values into the equilibrium expression gives
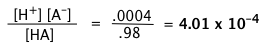
"Concentration of the acid" and [HA] are not the same
When dealing with problems involving acids or bases, bear in mind that when we speak of "the concentration", we usually mean the nominal or analytical concentration which is commonly denoted by Ca.
So for a solution made by combining 0.10 mol of pure formic acid HCOOH with sufficient water to make up a volume of 1.0 L, Ca = 0.10 M. However, we know that the concentration of the actual species [HCOOH] will be smaller the 0.10 M because some it ends up as the formate ion HCOO–. However, it will always be the case that the sum
[HCOOH] + [HCOO–] = Ca.
For the general case of an acid HA, we can write a mass balance equation
Ca = [HA] + [A–](1-16)
which reminds us the "A" part of the acid must always be somewhere!
Similarly, for a base B we can write
Cb = [B] + [HB+](1-17)
Degree of dissociation varies inversely with the concentration
If we represent the dissociation of a Ca M solution of a weak acid by
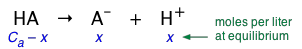 (1-18)
(1-18)
then its dissociation constant is given by
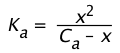 (1-19)
(1-19)
Because the Ca term is in the denominator here, we see that the amount of HA that dissociates varies inversely with the concentration; as Ca approaches zero, [HA] approaches Ca.
If we represent the fraction of the acid that is dissociated as
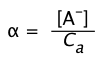 (1-20)
(1-20)
then Eq 8 becomes
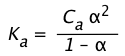 (1-21)
(1-21)
If the acid is sufficiently weak that x does not exceed 5% of Ca,
the -term in the denominator can be dropped, yielding
Ka ≈ Ca 2 (1-22)
Note that the above equations are also valid for weak bases if Kb and Cb are used in place of Ka and Ca.
Compare the percent dissociation of 0.10 M and .0010 M solutions of boric acid (\(K_a = 3.8 \times 10^{-10}\)).
Solution
Boric acid is sufficiently weak that we can use the approximation of Eq 1-22 to calculate a:= (5.8E–10 / .1)½ = 7.5E-5; multiply by 100 to get .0075 % diss. For the more dilute acid, a similar calculation yields 7.6E–4, or 0.76%.
2 Carrying out acid-base calculations
In Problem Example 1, we calculated the pH of a monoprotic acid solution, making use of an approximation in order to avoid the need to solve a quadratic equation. This raises the question: how "exact" must calculations of pH be? It turns out that the relation between pH and the nominal concentration of an acid, base, or salt (and especially arbitrary mixtures of these) can become quite complicated, requiring the solution of sets of simultaneous equations.
However, for almost all practical applications, one can make some approximations that simplify the math without detracting significantly from the accuracy of the results.
Equilibrium constants are rarely exactly known
As we pointed out in the preceding lesson, the "effective" value of an equilibrium constant (the activity) will generally be different from the value given in tables in all but the most dilute ionic solutions. Even if the acid or base itself is dilute, the presence of other "spectator" ions such as Na+ at concentrations much in excess of 0.001 M can introduce error.
The usual advice is to consider Ka values to be accurate to ±5 percent at best, and even more uncertain when total ionic concentrations exceed 0.1 M. As a consequence of this uncertainty, there is generally little practical reason to express the results of a pH calculation to more than two significant digits.
Finding the pH of a solution of a weak monoprotic acid
This is by far the most common type of problem you will encounter in a first-year Chemistry class. You are given the concentration of the acid, expressed as Ca moles/L, and are asked to find the pH of the solution. The very important first step is to make sure you understand the problem by writing down the equation expressing the concentrations of each species in terms of a single unknown, which we represent here by x:
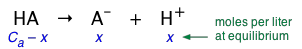 (2-1)
(2-1)
Substituting these values into the expression for \(K_a\), we obtain
 (2-2)
(2-2)
Don't bother to memorize these equations! If you understand the concept of mass balance on "A" expressed in (2-1), and can write the expression for Ka, you just substitute the x's into the latter, and you're off! If you feel the need to memorize stuff you don't need, it is likely that you don't really understand the material — and that should be a real worry!
In order to predict the pH of this solution, we must first find [H+], that is, x. The presence of terms in both x and x 2 here tells us that this is a quadratic equation. This can be rearranged into x 2 = Ka (1 – x) which, when written in standard polynomial form, becomes the quadratic
\[[\ce{H^{+}}]^2 – C_a [H^{+}] – K_w = 0 \label{2-3} \]
However, don't panic! As we will explain farther on, in most practical cases we can make some simplifying approximations which eliminate the need to solve a quadratic. And when, as occasionally happens, a quadratic is unavoidable, we will show you some relatively painless ways of dealing with it.
How to deal with Quadratic Equations
What you do will depend on what tools you have available. If you are only armed with a simple calculator, then there is always the venerable quadratic formula that you may have learned about in high school, but if at all possible, you should avoid it: its direct use in the present context is somewhat laborious and susceptible to error.
Use of the standard quadratic formula on a computer or programmable calculator can lead to weird results!
The reason for this is that if b2 >> |4ac|, one of the roots will require the subtraction of two terms whose values are very close; this can lead to considerable error when carried out by software that has finite precision.
One can get around this by computing the quantity
\[Q = –\dfrac{b + \pm (b) \sqrt{ b^2 – 4ac}}{2} \nonumber \]
from which the roots are x1= Q /a and x2 = c /Q. (See any textbook on numerical computing for more on this and other metnods.)
However, who want's to bother with this stuff in order to solve typical chemistry problems? Better to avoid quadratics altogether if at all possible!
Remember: there are always two values of x (two roots) that satisfy a quadratic equation. For all acid-base equilibrium calculations that are properly set up, these roots will be real, and only one will be positive; this is the one you take as the answer.
Approximations, judiciously applied, simplify the math
We have already encountered two of these approximations in the examples of the preceding section:
- In all but the most dilute solutions, we can assume that the dissociation of the acid HA is the sole source of H+, with the contribution due to water autoprotolysis being negligible.
- We were able to simplify the equilibrium expressions by assuming that the x-term, representing the quantity of acid dissociated, is so small compared to the nominal concentration of the acid Ca that it can be neglected. Thus in Problem Example 1, the term in the denominator that has the form (0.1 - x) , representing the equilibrium concentration of the undissociated acid, is replaced by 0.1.
Most people working in the field of practical chemistry will never encounter situations in which the first of these approximations is invalid. This is not the case, however, for the second one.
Should I drop the x, or forge ahead with the quadratic form?
If the acid is fairly concentrated (usually with Ca > 10–3 M) and sufficiently weak that most of it remains in its protonated form HA, then the concentration of H+ it produces may be sufficiently small that the expression for Ka reduces to
Ka ≈ [H+]2 / Ca
so that
[H+] ≈ (Ka Ca)½(2-4)
This can be a great convenience because it avoids the need to solve a quadratic equation. However, it also exposes you to the danger that this approximation may not be justified.
The usual advice is that if this first approximation of x exceeds 5 percent of the value it is being subtracted from (0.10 in the present case), then the approximation is not justified. We will call this the "five percent rule".
Problem Example 5 - pH and degree of dissociation
- Estimate the pH of a 0.20 M solution of acetic acid, Ka = 1.8 × 10–5.
- What percentage of the acid is dissociated?
Solution
For brevity, we will represent acetic acid CH3COOH as HAc, and the acetate ion by Ac–. As before, we set x = [H+] = [Ac–], neglecting the tiny quantity of H+ that comes from the dissociation of water.
Substitution into the equilibrium expression yields
\[K_a = x^2/(0.20 - x)
Can we simplify this by applying the approximation 0.20 – x ≈ 0.20 ? Looking at the number on the right side of this equation, we note that it is quite small. This means the left side must be equally small, which requires that the denominator be fairly large, so we can probably get away with dropping x. Doing so yields
(x2 / 0.20) = 1.8E-5 or x = (0.20 × 1.8E–5)½ = 1.9E-3 M
The "5 per cent rule" requires that the above result be no greater than 5% of 0.20, or 0.010. Because 0.0019 meets this condition, we can set
x = [H+] ≈ 1.9 × 10–3 M, and the pH will be –log (1.9 × 10–3) = 2.7
b) Percent dissociation: 100% × (1.9 × 10–3 M) / (0.20 M) = 0.95%
This plot shows the combinations of Ka and Ca that generally yield satisfactory results with the approximation of Eq 4.
Weak bases are treated in an exactly analogous way:
Methylamine CH3NH2 is a gas whose odor is noticed around decaying fish. A solution of CH3NH2 in water acts as a weak base. A 0.10 M solution of this amine in water is found to be 6.4% ionized. Use this information to find \Kb and pKb for methylamine.
Solution: When methylamine "ionizes", it takes up a proton from water, forming the methylaminium ion:
CH3NH2 + H2O → CH3NH3+ + OH–
Let x = [CH3NH3+] = [OH–] = .064 × 0.10 = 0.0064
[CH3NH2] = (0.10 – .064) = 0.094
Substitute these values into equilibrium expression for \Kb:
\[K_b = \frac{0.0064^2}{0.094} \nonumber \]
To make sure we can stop here, we note that (3.6E4 / .01) = .036; this is smaller than .05, so we pass the 5% rule and can use the approximation and drop the
x-term in the denominator.
pKb = – log \Kb = – log (4.4 × 10–10) = 3.36
However, one does not always get off so easily!
With a Ka of 0.010, HClO2 is one of the "stronger" weak acids, thanks to the two oxygen atoms whose electronegativity withdraws some negative charge from the chlorine atom, making it easier for the hydrogen to depart as a proton.
Find the pH of a 0.10 M solution of chloric acid in pure water.
\[0.010 = \frac{x^2}{0.10 - x} \nonumber \] (i)
The approximation 0.10 – x ≈ 0.10 gives us
x ≈ (Ka Ca)½ = (0.010 ×0.10)½ = (.001)½ = .032 (ii)
The difficulty, in this case, arises from the numerical value of Ka differing from the nominal concentration 0.10 M by only a factor of 10. As a result,
x / Ca = .032 / 0.10 = 0.32 which clearly exceeds the 5% limit; we have no choice but to face the full monte of the quadratic solution. (see Problem Example 8 below).
Successive approximations will get you there with minimal math
In the method of successive approximations, you start with the value of [H+] (that is, x) you calculated according to (2-4), which becomes the first approximation. You then substitute this into (2-2), which you solve to get a second approximation. This cycle is repeated until differences between successive answers become small enough to ignore.
Estimate the pH of a 0.10 M aqueous solution of HClO2, Ka = 0.010, using the method of successive approximations.
Solution: The equilibrium condition is
\[K_{\mathrm{a}} = \dfrac{x \cdot x}{c_{\mathrm{a}} - x} \nonumber \]
We solve this for x (neglecting the x in the denominator), resulting in the first approximation x1, and then successively plug each result into the previous equation, yielding approximations x2 and x3:
\[x_1 = \sqrt{K_{\mathrm{a}} \cdot c_\mathrm{a}} =0.032 \nonumber \]
\[x_2 = \sqrt{K_{\mathrm{a}} \cdot (c_\mathrm{a} - x_1)} =0.026 \nonumber \]
\[x_3 = \sqrt{K_{\mathrm{a}} \cdot (c_\mathrm{a} - x_2)} =0.027 \nonumber \]
The last two approximations x2 and x3 are within 5% of each other.
Note that if we had used x1 as the answer, the error would have been 18%.
(An exact numeric solution yields the roots 0.027016 and –0.037016)
Use a graphic calculator or computer to find the positive root
The real roots of a polynomial equation can be found simply by plotting its value as a function of one of the variables it contains.
In this example, the pH of a 10–6 M solution of hypochlorous acid (HOCl, Ka = 2.9E–8) was found by plotting the value of
y = ax2 + bx + c, whose roots are the two values of x that correspond to y = 0.
This method generally requires a bit of informed trial-and-error to make the locations of the roots visible within the scale of the axes.
Be lazy, and use an on-line quadratic equation solver
If you google "quadratic equation solver", you will find numerous on-line sites that offer quick-and-easy "fill-in-the-blanks" solutions.
Unfortunately, few of these will be useful for acid-base problems involving numbers that must be expressed in "E-notation" (e.g., 2.7E-11.) Of those that do, the one at the MathIsFun site is highly recommended; others can be found here and at the Quad2Deg site.
If you can access a quad equation solver on your personal electronic device or through the Internet, this is quick and painless. All you need to do is write the equation in polynomial form ax2 + bx + c = 0, insert values for
a, b, and c, and away you go!
This is so easy, that many people prefer to avoid the "5% test" altogether, and go straight to an exact solution. However, make sure can do the 5%-thing for exams where Internet-accessible devices are not permitted!
Estimate the pH of a 0.10 M aqueous solution of HClO2, Ka = 0.010.
Solution
The reaction equation HClO2 → H+ + ClO2– defines the equilibrium expression
\[0.010 = \dfrac{x \cdot x}{0.10 - x} \nonumber \]
Multiplying by the denominator yields
x2 = 0.010 × (0.10 – x) = .0010 – .01 x which we arrange into standard polynomial form:
x2 + 0.01 x – 0.0010 = 0
Entering the coefficients {1 .01 –.001} into an online quad solver yields the roots
.027 and –.037. Taking the positive one, we have [H+] = .027 M;
the solution pH is – log .027 = 1.6.
Note: a common error is to forget to enter the minus sign for the last term; try doing this and watch the program blow up!
Avoid math altogether and make a log-C vs pH plot
This is not only simple to do (all you need is a scrap of paper and a straightedge), but it will give you far more insight into what's going on, especially in polyprotic systems. All explained in Section 3 of the next lesson.
Solutions of salts
Most salts do not form pH-neutral solutions
Salts such as sodium chloride that can be made by combining a strong acid (HCl) with a strong base (NaOH, KOH) have a neutral pH, but these are exceptions to the general rule that solutions of most salts are mildly acidic or alkaline.
Salts of a strong base and a weak acid yield alkaline solutions.
"Hydro-lysis" literally means "water splitting", as exemplified by the reaction A– + H2O → HA + OH–. The term describes what was believed to happen prior to the development of the Brønsted-Lowry proton transfer model.
This important property has historically been known as hydrolysis — a term still used by chemists.
Some examples:
- Potassium Cyanide
- KCN can be thought of the salt made by combining the strong base KOH with the weak acid HCN: K+ + OH– → KOH. When solid KCN dissolves in water, this process is reversed, yielding a solution of the two ions. K+, being a "strong ion", does not react with water. However, the "weak ion" CN–, being the conjugate base of a weak acid, will have a tendency to abstract protons from water: CN– + H2O → HCN + OH–, causing the solution to remain slightly alkaline.
- Sodium bicarbonate
- NaHCO3 (more properly known as sodium hydrogen carbonate) dissolves in water to yield a solution of the hydrogen carbonate ion HCO3–. This ion is an ampholyte — that is, it is both the conjugate base of the weak carbonic acid H2CO3, as well as the conjugate acid of the carbonate ion CO32–:
The HCO3– ion is therefore amphiprotic: it can both accept and donate protons, so both processes take place:
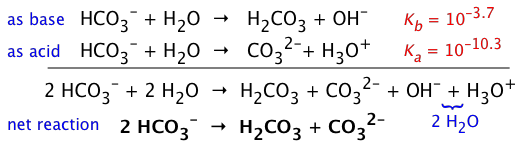
However, if we compare the Ka and Kb of HCO3–, it is apparent that its basic nature wins out, so a solution of NaHCO3 will be slightly alkaline. (The value of pKb is found by recalling that Ka + Kb = 14.)
- Sodium acetate
- A solution of CH3COONa serves as a model for the strong-ion salt of any organic acid, since all such acids are weak: CH3COO– + H2O → CH3COOH + OH–
Salts of most cations (positive ions) give acidic solutions
The protons can either come from the cation itself (as with the ammonium ion NH4+), or from waters of hydration that are attached to a metallic ion.
This latter effect happens with virtually all salts of metals beyond Group I; it is especially noticeable for salts of transition ions such as hexaaquoiron(III) ("ferric ion"):
Fe(H2O)63+ → Fe(H2O)5OH2+ + H+ (2-5)
This comes about because the positive field of the metal enhances the ability of H2O molecules in the hydration shell to lose protons. In the case of the hexahyrated ion shown above, a whose succession of similar steps can occur, but for most practical purposes only the first step is significant.
Find the pH of a 0.15 M solution of aluminum chloride.
Solution
The aluminum ion exists in water as hexaaquoaluminum Al(H2O)63+, whose pKa = 4.9, Ka = 10–4.9 = 1.3E–5. Setting x = [H+] = [Al(H2O)5OH 2+], the equilibrium expression is
Using the above approximation, we get
x ≈ (1.96E–6)½ = 1.4E–3, corresponding to pH = 2.8.
Finally, we compute x/Ca = 1.4E–3 ÷ 0.15 = .012 confirming that we are within the "5% rule".
The only commonly-encountered salts in which the proton is donated by the cation itself are those of the ammonium ion:
\[\ce{NH_4^{+}→ NH)3(aq) + H^{+}\lable{2-6} \nonumber \]
Calculate the pH of a 0.15 M solution of NH4Cl. The ammonium ion Ka is 5.5E–10.
Solution
According to Eq 6 above, we can set [NH3] = [H+] = x, obtaining the same equilibrium expression as in the preceding problem.
Because Ka is quite small, we can safely use the approximation 0.15 - 1 ≈ .015, which yields pH = –log 0.90E–5 = 5.0
Most salts of weak acids form alkaline solutions
As indicated in the example, such equilibria strongly favor the left side; the stronger the acid HA, the less alkaline the salt solution will be.
Because an ion derived from a weak acid such as HF is the conjugate base of that acid, it should not surprise you that a salt such as NaF forms an alkaline solution, even if the equilibrium greatly favors the left side::
F– + H2O HF + OH–(2-7)
Solution of sodium fluoride
Find the pH of a 0.15 M solution of NaF. (HF Ka = 6.7E–4)
Solution: The reaction is F- + H2O = HF + OH–; because HF is a weak acid, the equilibrium strongly favors the right side. The usual approximation yields
However, on calculating x/Ca = .01 ÷ 0.15 = .07, we find that this does not meet the "5% rule" for the validity of the approximation. We therefore expand the equilibrium expression
into standard polynomial form x2 + 6.7E–4 x – 1.0E–4 = 0 and enter the coefficients {1 6.7E–4 –.0001} into a quadratic solver. This yields the positive root x = 0.0099 which turns out to be sufficiently close to the approximation that we could have retained it after all.. perhaps 5% is a bit too restrictive for 2-significant digit calculations!
What about a salt of a weak acid and a weak base?
A salt of a weak acid gives an alkaline solution, while that of a weak base yields an acidic solution. What happens if we dissolve a salt of a weak acid and a weak base in water? Ah, this can get a bit tricky! Nevertheless, this situation arises very frequently in applications as diverse as physiological chemistry and geochemistry.
As an example of how one might approach such a problem, consider a solution of ammonium formate, which contains the ions NH4+ and HCOO-. Formic acid, the simplest organic acid, has a pKa of 3.7; for NH4+, pKa = 9.3.
Three equilibria involving these ions are possible here; in addition to the reactions of the ammonium and formate ions with water, we must also take into account their tendency to react with each other to form the parent neutral species:
| NH4+ → NH3 + H+ | K1 = 10–9.3 |
| HCOO– + H2O → HCOOH + OH– | K2 = (1O–14/10–3.7) = 10–10.3 |
| NH4+ + HCOO– → NH3 + HCOOH | K3 |
Inspection reveals that the last equation above is the sum of the first two,plus the reverse of the dissociation of water
| H+ + OH– → H2O | K4 = 1/Kw |
The value of K3 is therefore
(2-8)
A rigorous treatment of this system would require that we solve these equations simultaneously with the charge balance and the two mass balance equations. However, because K3 is several orders of magnitude greater than K1 or K2, we can greatly simplify things by neglecting the other equilibria and considering only the reaction between the ammonium and formate ions.
Notice that the products of this reaction will tend to suppress the extent of the first two equilibria, reducing their importance even more than the relative values of the equilibrium constants would indicate.
ammonium formate
Estimate the pH of a 0.0100 M solution of ammonium formate in water.
Solution: From the stoichiometry of HCOONH4,
[NH4+] = [HCOO–] and [NH3] = [HCOOH] (i)
then, from Eq 8 above,
![]() (ii)
(ii)
in which Kb is the base constant of ammonia, Kw /10–9.3.
From the formic acid dissociation equilibrium we have
(iii)
We now rewrite the expression for K3
![]() (iv)
(iv)
which yields
(v)
and thus the pH is 6.5
What is interesting about this last example is that the pH of the solution is apparently independent of the concentration of the salt. If Ka = Kb, then this is always true and the solution will be neutral (neglecting activity effects in solutions of high ionic strength). Otherwise, it is only an approximation that remains valid as long as the salt concentration is substantially larger than the magnitude of either equilibrium constant. Clearly, the pH of any solution must approach that of pure water as the solution becomes more dilute.
Salts of analyte ions
Polyprotic acids form multiple anions; those that can themselves donate protons, and are thus amphiprotic, are called analytes. The most widely known of these is the bicarbonate (hydrogen carbonate) ion, HCO3–, which we commonly know in the form of its sodium salt NaHCO3 as baking soda.
The other analyte series that is widely encountered, especially in biochemistry, is those derived from phosphoric acid:
\[\mathrm{H}_3 \mathrm{PO}_4 \xrightarrow[10^{-2.12}]{K_1} \mathrm{H}_2 \mathrm{PO}_4^{-} \xrightarrow{10^{-7.2}} \mathrm{KPO}_4{ }^{2-} \frac{K_3}{10^{-12.3}} \mathrm{PO}_4^{3-} \nonumber \]
The solutions of analyte ions we most often need to deal with are the of "strong ions", usually Na+, but sometimes those of Group 2 cations such as Ca2+.
The exact treatment of these systems is generally rather complicated, but for the special cases in which the successive Ka's of the parent acid are separated by several orders of magnitude (as in the two systems illustrated above), a series of approximations reduces the problem to the simple expression
\[\left[\mathrm{H}^{+}\right] \approx \sqrt{K_1 K_2} \label{2-9} \]
which, you will notice, as with the salt of a weak acid and a weak base discussed in the preceding subsection predicts that the pH is independent of the salt's concentration. This, of course, is a sure indication that this treatment is incomplete. Fortunately, however, it works reasonably well for most practical purposes, which commonly involve buffer solutions.
When dealing with acid-base systems having very small Ka's, and/or solutions that are extremely dilute, it may be necessary to consider all the species present in the solution, including minor ones such as OH–.
This is almost never required in first-year courses. However, for students in more advanced courses, this "comprehensive approach" (as it is often called) illustrates the important general methodology of dealing with more complex equilibrium problems. It also shows explicitly how making various approximations gradually simplifies the treatment of more complex systems.
Solutions of polyprotic acids
A diprotic acid H2A can donate its protons in two steps:
\[\ce{H2A → HA^{–} →HA^{–}} \nonumber \]
and similarly, for a tripotic acid H3A:
\[\ce{H3A → H2A^{–} → HA^{2–} → A^{3–}} \nonumber \]
In general, we can expect Ka2 for the "second ionization" to be smaller than Ka1 for the first step because it is more difficult to remove a proton from a negatively charged species. The magnitude of this difference depends very much on whether the two removable protons are linked to the same atom, or to separate atoms spaced farther apart.
Some polyprotic acids you should know
These acids are listed in the order of decreasing Ka1. The numbers above the arrows show the successive Ka's of each acid.
- Notice how successive Ka's of each acid become smaller, and how their ratios relate to the structures of each acid.
- Sulfuric acid is the only strong polyprotic acid you are likely to encounter.
- Sulfurous acid has never been detected; what we refer to as H2SO3 is more properly represented as a hydrated form of sulfur dioxide: which dissociates into the hydrosulfite ion:
SO2·H2O → HSO3– + H+ . The ion HSO3– exists only in solution; solid bisulfite salts are not known. - Similarly, pure carbonic acid has never been isolated, but it does exist as a minority species in an aqueous solution of CO2: [CO2(aq)] = 650[H2CO3]. The formula H2CO3 ordinarily represents the combination CO2(aq) and "true" H2CO3. The latter is actually about a thousand times stronger than is indicated by the pKa of 6.3, which is the weighted average of the equilibrium mixture.
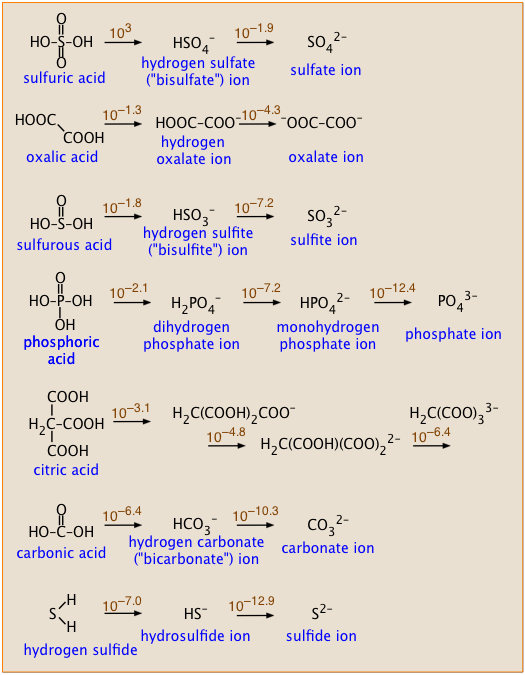
Compare the successive pKa values of sulfuric and oxalic acids (see their structures in the box, above right), and explain why they should be so different.
Solution
The two pKa values of sulfuric acid differ by 3.0 – (–1.9) = 4.9, whereas for oxalic acid the difference is 1.3 – (–4.3) = 3.0. That's a difference of almost 100 between the two Ka's. Removal of a second proton from a molecule that already carries some negative charge is always expected to be less favorable energetically. In sulfuric acid, the two protons come from –OH groups connected to the same sulfur atom, so the negative charge that impedes loss of the second proton is more localized near the site of its removal. In oxalic acid, the two protons are removed from –OH groups attached to separate carbon atoms, so the negative charge of the mono-negative ions will exert less restraint on loss of the second proton.
Solutions of polyprotic acids in pure water
With the exception of sulfuric acid (and some other seldom-encountered strong diprotic acids), most polyprotic acids have sufficiently small Ka1 values that their aqueous solutions contain significant concentrations of the free acid as well as of the various dissociated anions.
Thus for a typical diprotic acid H2A, we must consider the three coupled equilibria
\[\ce{H_2A → H^+ + HA^{–} } \tag{K1} \]
\[\ce{HA^{–} → H^{+} + HA^{2–}} \tag{K2} \]
\[\ce{H_2O → H^{+} + OH^{–} } \tag{Kw} \]
An exact treatment of such a system of four unknowns \(\ce{[H2A]}\), \(\ce{[HA^{–}]}\), \(\ce{[A^{2–}]}\) and \(\ce{[H^{+}]}\) requires the solution of a quartic equation. If we include \(\ce{[OH^{–}]}\), it's even worse!
In most practical cases, we can make some simplifying approximations:
- Unless the solution is extremely dilute or \(K_1\) (and all the subsequent K's) are extremely small, we can forget that any hydroxide ions are present at all.
- If \(K_1\) is quite small, and the ratios of succeeding K's are reasonably large, we may be able, without introducing too much error, to neglect the other K's and treat the acid as monoprotic.
In addition to the three equilibria listed above, a solution of a polyprotic acid in pure water is subject to the following two conditions:
Material balance: although the distribution of species between the acid form \(\ce{H2A}\) and its base forms \(\ce{HAB^{–}}\) and \(\ce{A^{2–}}\) may vary, their sum (defined as the "total acid concentration" \(C_a\) is a constant for a particular solution:
\[C_a = [H_2A] + [HA^{–}] + [A^{2–}] \nonumber \]
Charge balance: The solution may not possess a net electrical charge:
\[[\ce{H3O^{+}}] = [\ce{OH^{–}}] + [\ce{HA^{–}}] + 2 [\ce{A^{2–}}] \nonumber \]
Why do we multiply \(\ce{[A^{2–}]}\) by 2? Two moles of \(\ce{H3O^{+}}\) are needed in order to balance out the charge of 1 mole of \(\ce{A^{2–}}\).
Simplified treatment of polyprotic acid solutions
The calculations shown in this section are all you need for the polyprotic acid problems encountered in most first-year college chemistry courses. More advanced courses may require the more exact methods in Lesson 7.
Because the successive equilibrium constants for most of the weak polyprotic acids we ordinarily deal with diminish by several orders of magnitude, we can usually get away with considering only the first ionization step. To the extent that this is true, there is nothing really new to learn here. However, without getting into a lot of complicated arithmetic, we can often go farther and estimate the additional quantity of H+ produced by the second ionization step.
a) Calculate the pH of a 0.050 M solution of CO2 in water.
For H2CO3, K1 = 10–6.4 = 4.5E–7, K2 = 10–10.3 = 1.0E–14.
b) Estimate the concentration of carbonate ion CO32– in the solution.
Solution
a) Because K1 and K2 differ by almost four orders of magnitude, we will initially neglect the second dissociation step. Because this latter step produces only a tiny additional concentration of H+, we can assume that [H+] = [HCO3–] = x:
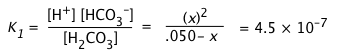 (i)
(i)
Can we further simplify this expression by dropping the x in the denominator? Let's try:
x = [0.05 × (4.5E–7)]½ = 1.5E–4.
Applying the "5-percent test", the quotient x/Ca must not exceed 0.05. Working this out yields (1.5E–4)/(.05) = .003, so we can avoid a quadratic.
x = [H+] ≈ (KaCa)½ = [(4.5E–7) × .01]½ = (.001)½ = 0.032 M,
and the
pH = – log .032 = 1.5.
b) We now wish to estimate [CO32–] ≡ x.
Examining the second dissociation step, it is evident that this will consume x mol/L of HCO3–, and produce an equivalent amount of H+ which adds to the quantity we calculated in (a).
 (ii)
(ii)
Owing to the very small value of K2 compared to K1, we can assume that the concentrations of HCO3– and H+ produced in the first dissociation step will not be significantly altered in this step. This allows us to simplify the equilibrium constant expression and solve directly for [CO32–]:
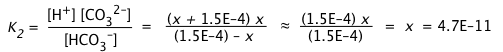 (iii)
(iii)
It is of course no coincidence that this estimate of [CO32–] yields a value identical with K2; this is entirely a consequence of the simplifying assumptions we have made. Nevertheless, as long as K2 << K1 and the solution is not highly dilute, the result will be sufficiently accurate for most purposes.
Sulfuric acid: A Special Case
Although this is a strong acid, it is also diprotic, and in its second dissociation step it acts as a weak acid. Because sulfuric acid is so widely employed both in the laboratory and industry, it is useful to examine the result of taking its second dissociation into consideration.
Estimate the pH of a 0.010 M solution of H2SO4 with K1 = 103 and K2 = 0.012
Solution:
Because K1 > 1, we can assume that a solution of this acid will be completely dissociated into H3O+ and bisulfite ions HSO4–. Thus the only equilibrium we need to consider is the dissociation of a 0.010 M solution of bisulfite ions.
\[\ce{HSO4^{–} + H2O → SO4^{2–} + H3O^{+}} \nonumber \]
\[K_2=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{SO}_4{ }^{2-}\right]}{\left[\mathrm{HSO}_4{ }^{-}\right]}=\frac{(x)^2}{.010-x}=0.012 \nonumber \]
Setting \(\ce{[H^{+}] = [SO4^{2–}] = x}\), and dropping \(x\) from the denominator, yields
\[x ≈ \sqrt{(0.010)(0.012)} = \sqrt{1.2 \times 10^{-4}} = 0.0011 \nonumber \]
Applying the "five percent rule", we find that x / Ca = .0011/.01 = .11 which is far over the allowable error, so we must proceed with the quadratic form. Rewriting the equilibrium expression in polynomial form gives
\[x^2 + 0.022x – 1.2 \times 10^{–4} = 0 \nonumber \]
Inserting the coefficients {1 .022 .000012} into a quad-solver utility yields the roots \(4.5 \times 10^{–3}\) and \(–0.0027\). Taking the positive root, we obtain
\[pH = –\log (0.0045) = 2.3 \nonumber \]
Thus the second "ionization" of \(\ce{H2SO4}\) has only reduced the pH of the solution by 0.1 unit from the value (2.0) it would theoretically have if only the first step were considered.
Amino acids and Zwitterions
Zwitterions: molecular hermaphrodites
Amino acids, the building blocks of proteins, contain amino groups –NH2 that can accept protons, and carboxyl groups –COOH that can lose protons. Under certain conditions, these events can occur simultaneously, so that the resulting molecule becomes a “double ion” which goes by its German name Zwitterion.
Glycine: the simplest amino acid
The simplest of the twenty natural amino acids that occur in proteins is glycine H2N–CH2–COOH, which we use as an example here.
Solutions of glycine are distributed between the acidic-, zwitterion-, and basic species:
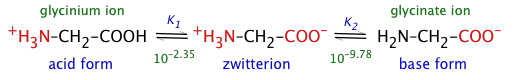 (3-1)
(3-1)
In the following development, we use the abbreviations H2Gly+ (glycinium), HGly (zwitterion), and Gly– (glycinate) to denote the dissolved forms.
The two acidity constants are
\[K_1=\frac{\left[\mathrm{H}^{+}\right][\text {HGly }]}{\left[\mathrm{H}_2 \mathrm{Gly}^{+}\right]}=10^{-2.25} \label{3-2A} \]
and
\[K_2=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{Gly}^{-}\right]}{[\mathrm{HGly}]}=10^{-9.78} \label{3-2B} \]
If glycine is dissolved in water, charge balance requires that
\[H_2Gly^+ + [H^+] \rightleftharpoons [Gly^–] + [OH^–] \label{3-3} \]
Substituting the equilibrium constant expressions (including that for the autoprotolysis of water) into the above relation yields
\[\frac{\left[\mathrm{H}^{+}\right][\mathrm{HGly}]}{K_1}+\left[\mathrm{H}^{+}\right]=\frac{K_2[\mathrm{HGly}]}{\left[\mathrm{H}^{+}\right]}+\frac{K_w}{\left[\mathrm{H}^{+}\right]} \label{3-4)} \]
Calculate the pH and the concentrations of the various species in a 0.100 M solution of glycine.
Solution
Substitution into Eq 4 above yields
\[\left[\mathrm{H}^{+}\right]=\sqrt{\frac{10^{-9.8} \times 0.10+10^{-14}}{0.1 /\left(10^{-2.3}+1\right)}}=10^{-6.1} \tag{i} \]
The concentrations of the acid and base forms are found from their respective equilibrium constant expressions (Eqs 2):
\[\left[\mathrm{H}_2 \mathrm{Gly}^{+}\right]=\frac{\left[\mathrm{H}^{+}\right] \times 0.10}{10^{-2.3}}=10^{-4.7} \tag{ii} \]
\[\left[\mathrm{Gly}^{-}\right]=\frac{10^{-9.8} \times 0.10}{\left[\mathrm{H}^{+}\right]}=10^{-4.7} \tag{iii} \]
The small concentrations of these singly-charged species in relation to \(C_a = 0.10\) shows that the zwitterion is the only significant glycine species in the solution.
If Equations ii and iii in this Example are recalculated for a range of pH values, one can plot the concentrations of each species against pH for 0.10 M glycine in water:



