9.6: The Hybrid Orbital Model
- Page ID
- 3518
- Explain why the sharing of atomic orbitals (as implied in the Lewis model) cannot adequately account for the observed bonding patterns in simple molecules.
- Sketch out a diagram illustrating how the plots of atomic s- and p- orbital wave functions give rise to a pair of hybrid orbitals.
- Draw "orbital box" diagrams showing how combinations of an atomic s orbital and various numbers of p orbitals create sp, sp2, and sp3 hybrid orbitals.
- Show how hybrid orbitals are involved in the molecules methane, water, and ammonia.
As useful and appealing as the concept of the shared-electron pair bond is, it raises a somewhat troubling question that we must sooner or later face: what is the nature of the orbitals in which the shared electrons are contained? Up until now, we have been tacitly assuming that each valence electron occupies the same kind of atomic orbital as it did in the isolated atom. As we shall see below, his assumption very quickly leads us into difficulties.
Atomic orbitals alone do not work for Molecules
Consider how we might explain the bonding in a compound of divalent beryllium, such as beryllium hydride, BeH2. The beryllium atom, with only four electrons, has a configuration of 1s22s2. Note that the two electrons in the 2s orbital have opposite spins and constitute a stable pair that has no tendency to interact with unpaired electrons on other atoms.
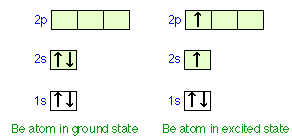
The only way that we can obtain two unpaired electrons for bonding in beryllium is to promote one of the 2s electrons to the 2p level. However, the energy required to produce this excited-state atom would be sufficiently great to discourage bond formation. It is observed that Be does form reasonably stable bonds with other atoms. Moreover, the two bonds in BeH2 and similar molecules are completely equivalent; this would not be the case if the electrons in the two bonds shared Be orbitals of different types, as in the "excited state" diagram above.
These facts suggest that it is incorrect to assume that the distribution of valence electrons that are shared with other atoms can be described by atomic-type s, p, and d orbitals at all.
Remember that these different orbitals arise in the first place from the interaction of the electron with the single central electrostatic force field associated with the positive nucleus. An outer-shell electron in a bonded atom will be under the influence of a force field emanating from two positive nuclei, so we would expect the orbitals in the bonded atoms to have a somewhat different character from those in free atoms. In fact, as far as valence electrons are concerned, we can throw out the concept of atomic orbital altogether and reassign the electrons to a new set of molecular orbitals that are characteristic of each molecular configuration. This approach is indeed valid, but we will defer a discussion of it until a later unit.
For now, we will look at a less-radical model that starts out with the familiar valence-shell atomic orbitals, and allows them to combine to form hybrid orbitals whose shapes conform quite well to the bonding geometry that we observe in a wide variety of molecules.
What are hybrid orbitals?
First, recall that the electron, being a quantum particle, cannot have a distinct location; the most we can do is define the region of space around the nucleus in which the probability of finding the electron exceeds some arbitrary value, such as 90% or 99%. This region of space is the orbital. Because of the wavelike character of matter, the orbital corresponds to a standing wave pattern in 3-dimensional space which we can often represent more clearly in 2-dimensional cross section. The quantity that is varying (“waving”) is a number denoted by ψ (psi) whose value varies from point to point according to the wave function for that particular orbital.
Orbitals of all types are simply mathematical functions that describe particular standing-wave patterns that can be plotted on a graph but have no physical reality of their own. Because of their wavelike nature, two or more orbitals (i.e., two or more functions ψ) can be combined both in-phase and out-of-phase to yield a pair of resultant orbitals which, to be useful, must have squares that describe actual electron distributions in the atom or molecule.
The s,p,d and f orbitals that you are familiar with are the most convenient ones for describing the electron distribution in isolated atoms because assignment of electrons to them according to the usual rules always yields an overall function Ψ2 that predicts a spherically symmetric electron distribution, consistent with all physical evidence that atoms are in fact spherical. For atoms having more than one electron, however, the s,p,d, f basis set is only one of many possible ways of arriving at the same observed electron distribution. We use it not because it is unique, but because it is the simplest.
In the case of a molecule such as BeH2, we know from experimental evidence that the molecule is linear and therefore the electron density surrounding the central atom is no longer spherical, but must be concentrated along two directions 180° apart, and we need to construct a function Ψ2 having these geometrical properties. There are any number of ways of doing this, but it is convenient is to use a particular set of functions ψ (which we call hybrid orbitals) that are constructed by combining the atomic s,p,d,and f functions that are already familiar to us.
You should understand that hybridization is not a physical phenomenon; it is merely a mathematical operation that combines the atomic orbitals we are familiar with in such a way that the new (hybrid) orbitals possess the geometric and other properties that are reasonably consistent with what we observe in a wide range (but certainly not in all) molecules. In other words, hybrid orbitals are abstractions that describe reality fairly well in certain classes of molecules (and fortunately, in much of the very large class of organic substances) and are therefore a useful means of organizing a large body of chemical knowledge... but they are far from infallible.
Hybridization is not a physical phenomenon; it is merely a mathematical operation that combines the atomic orbitals we are familiar with in such a way that the new (hybrid) orbitals possess the geometric and other properties that are reasonably consistent with what we observe in a wide range (but certainly not in all) molecules.
This approach, which assumes that the orbitals remain more or less localized on one central atom, is the basis of the theory which was developed in the early 1930s, mainly by Linus Pauling.
Linus Pauling (1901-1994) was the most famous American chemist of the 20th century and the author of the classic book The Nature of the Chemical Bond. His early work pioneered the application of X-ray diffraction to determine the structure of complex molecules; he then went on to apply quantum theory to explain these observations and predict the bonding patterns and energies of new molecules. Pauling, who spent most of his career at Cal Tech, won the Nobel Prize for Chemistry in 1954 and the Peace Prize in 1962.
"In December 1930 Pauling had his famous 'breakthrough' where, in a rush of inspiration, he 'stayed up all night, making, writing out, solving the equations, which were so simple that I could solve them in a few minutes'. This flurry of calculations would eventually become the first of Pauling's germinal series of papers on the nature of the chemical bond. 'I just kept getting more and more euphorious as time went by', Pauling would recall. "
Although the hybrid orbital approach has proven very powerful (especially in organic chemistry), it does have its limitations. For example, it predicts that both H2O and H2S will be tetrahedrally coordinated bent molecules with bond angles slightly smaller than the tetrahedral angle of 109.5° owing to greater repulsion by the nonbonding pair. This description fits water (104.5°) quite well, but the bond angle in hydrogen sulfide is only 92°, suggesting that atomic p orbitals (which are 90° apart) provide a better description of the electron distribution about the sulfur atom than do sp3 hybrid orbitals.
The hybrid orbital model is fairly simple to apply and understand, but it is best regarded as one special way of looking at a molecule that can often be misleading. Another viewpoint, called the molecular orbital theory, offers us a complementary perspective that it is important to have if we wish to develop a really thorough understanding of chemical bonding in a wider range of molecules.
Constructing hybrid orbitals
Below: "Constructive" and "destructive" combinations of 2p and 2s wave functions (line plots) give rise to the sp hybrid function shown at the right. The solid figures depict the corresponding probability functions ψ2.
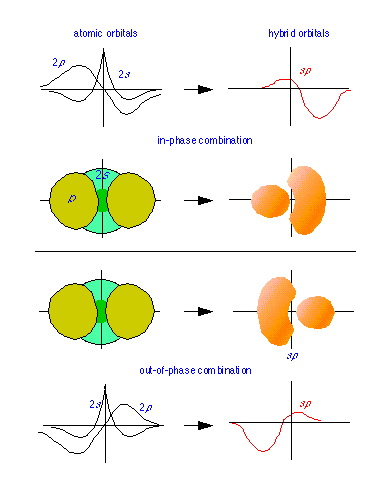
Hybrid orbitals are constructed by combining the ψ functions for atomic orbitals. Because wave patterns can combine both constructively and destructively, a pair of atomic wave functions such as the s- and p- orbitals shown at the left can combine in two ways, yielding the sp hybrids shown.
From an energy standpoint, we can represent the transition from atomic s- and p-orbitals to an sp hybrid orbital in this way:
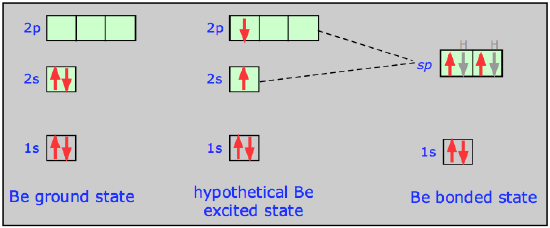
Notice here that 1) the total number of occupied orbitals is conserved, and 2) the two sp hybrid orbitals are intermediate in energy between their parent atomic orbitals. In terms of plots of the actual orbital functions ψ we can represent the process as follows:
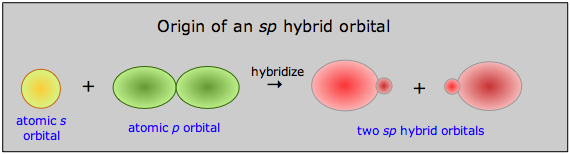
The probability of finding the electron at any location is given not by ψ, but by ψ2, whose form is roughly conveyed by the solid figures in this illustration.
Hybrids derived from atomic s- and p orbitals
Digonal bonding: sp-hybrid orbitals
Returning to the example of BeH2, we can compare the valence orbitals in the free atoms with those in the beryllium hydride molecule as shown here. It is, of course, the overlap between the hydrogen-1s orbitals and the two lobes of the beryllium sp-hybrid orbitals that constitutes the two Be—H "bonds" in this molecule. Notice that whereas a single p-orbital has lobes on both sides of the atom, a single sp-hybrid has most of its electron density on one side, with a minor and more spherical lobe on the other side. This minor lobe is centered on the central atom (some textbook illustrations don't get this right.)
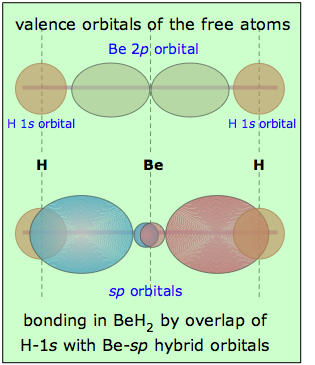
As far as the shape of the molecule is concerned, the result is exactly the same as predicted by the VSEPR model (although hybrid orbital theory predicts the same result in a more fundamental way.) We can expect any central atom that uses sp-hybridization in bonding to exhibit linear geometry when incorporated into a molecule.
Trigonal (sp2) hybridization
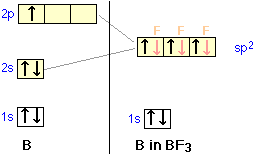
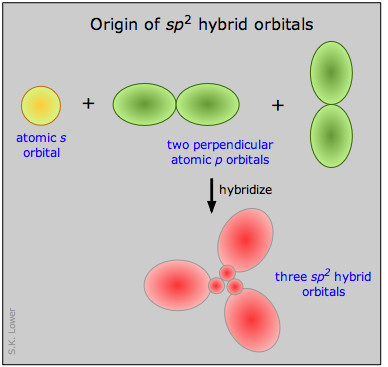
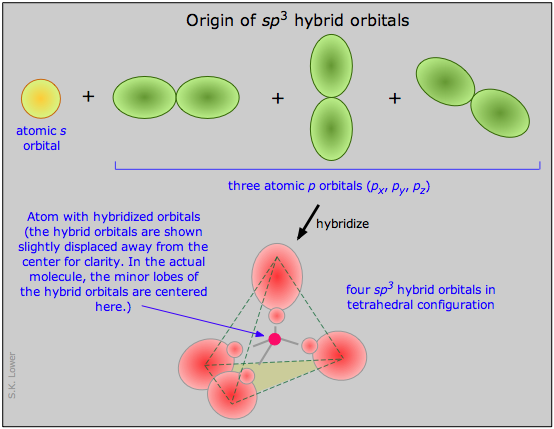
We can now go on to apply the same ideas to some other simple molecules. In boron trifluoride, for example, we start with the boron atom, which has three outer-shell electrons in its normal or ground state, and three fluorine atoms, each with seven outer electrons. As is shown in this configuration diagram, one of the three boron electrons is unpaired in the ground state. In order to explain the trivalent bonding of boron, we postulate that the atomic s- and p- orbitals in the outer shell of boron mix to form three equivalent hybrid orbitals. These particular orbitals are called sp2 hybrids, meaning that this set of orbitals is derived from one s- orbital and two p-orbitals of the free atom.
This illustration shows how an s-orbital mixes with two p orbitals to form a set of three sp2 hybrid orbitals. Notice again how the three atomic orbitals yield the same number of hybrid orbitals.
Boron Trifluoride BF3 is a common example of sp2 hybridization. The molecule has plane trigonal geometry.

Tetrahedral (sp3) hybridization
Let us now look at several tetravalent molecules, and see what kind of hybridization might be involved when four outer atoms are bonded to a central atom. Perhaps the commonest and most important example of this bond type is methane, CH4.
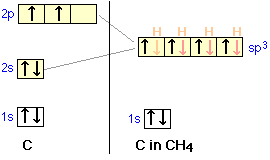
orbitals of carbon mix into four sp3 hybrid orbitals which are chemically and geometrically identical; the latter condition implies that the four hybrid orbitals extend toward the corners of a tetrahedron centered on the carbon atom.
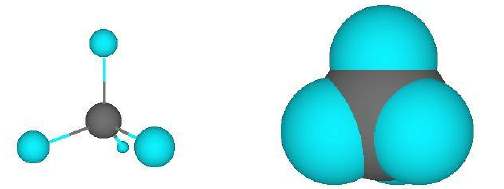
Methane is the simplest hydrocarbon; the molecule is approximately spherical, as is shown in the space-filling model:
By replacing one or more of the hydrogen atoms in CH4 with another sp3 hybridized carbon fragments, hydrocarbon chains of any degree of complexity can be built up. The simplest of these is ethane:
This shows how an sp3 orbital on each of two two carbon atoms join (overlap) to form a carbon-carbon bond, and then the remaining carbon sp3 orbital overlaps with six hydrogen 1s orbitals to form the ethane molecule.
Lone pair electrons in hybrid orbitals
If lone pair electrons are present on the central atom, these can occupy one or more of the sp3 orbitals. This causes the molecular geometry to be different from the coordination geometry, which remains tetrahedral. In the ammonia molecule, for example, the nitrogen atom normally has three unpaired p electrons, but by mixing the 2s and 2p orbitals, we can create four sp3-hybrid orbitals just as in carbon. Three of these can form shared-electron bonds with hydrogen, resulting in ammonia, NH3. The fourth of the sp3 hybrid orbitals contains the two remaining outer-shell electrons of nitrogen which form a non-bonding lone pair. In acidic solutions these can coordinate with a hydrogen ion, forming the ammonium ion NH4+.
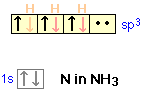

Although no bonds are formed by the lone pair in NH3, these electrons do give rise to a charge cloud that takes up space just like any other orbital.
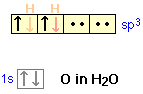
In the water molecule, the oxygen atom can form four sp3 orbitals. Two of these are occupied by the two lone pairs on the oxygen atom, while the other two are used for bonding. The observed H-O-H bond angle in water (104.5°) is less than the tetrahedral angle (109.5°); one explanation for this is that the non-bonding electrons tend to remain closer to the central atom and thus exert greater repulsion on the other orbitals, thus pushing the two bonding orbitals closer together.
Molecular ions
Hybridization can also help explain the existence and structure of many inorganic molecular ions. Consider, for example, electron configurations of zinc in the compounds in the illustrations below. The tetrachlorozinc ion (top row) is another structure derived from zinc and chlorine. As we might expect, this ion is tetrahedral; there are four chloride ions surrounding the central zinc ion. The zinc ion has a charge of +2, and each chloride ion is –1, so the net charge of the complex ion is –2.
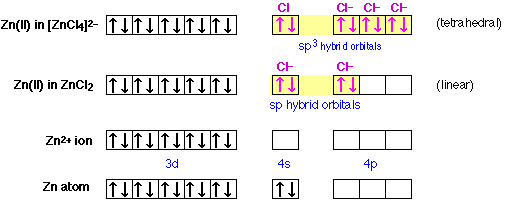
At the bottom is shown the electron configuration of atomic zinc, and just above it, of the divalent zinc ion. Notice that this ion has no electrons at all in its 4-shell. In zinc chloride, shown in the next row up, there are two equivalent chlorine atoms bonded to the zinc. The bonding orbitals are of sp character; that is, they are hybrids of the 4s and one 4p orbital of the zinc atom. Since these orbitals are empty in the isolated zinc ion, the bonding electrons themselves are all contributed by the chlorine atoms, or rather, the chloride ions, for it is these that are the bonded species here. Each chloride ion possesses a complete octet of electrons, and two of these electrons occupy each sp bond orbital in the zinc chloride complex ion. This is an example of a coordinate covalent bond, in which the bonded atom contributes both of the electrons that make up the shared pair.


