8.10.9B: The nature of ions in aqueous solution
- Page ID
- 20110
The kinds of ions we will consider in this lesson are mostly those found in solutions of common acids or salts. As is evident from the image below, most of the metallic elements form monatomic cations, but the number of monatomic anions is much smaller. This reflects the fact that many single-atom anions such as hydride H–, oxide O2–, sulfide S2– and those in Groups 15 and 16, are unstable in (i.e., react with) water, and their major forms are those in which they are combined with other elements, particularly oxygen. Some of the more familiar oxyanions are hydroxide OH–, carbonate CO32–, nitrate NO3–, sulfate SO42–, chlorate ClO42–, and arsenate AsO42–.
Conductivity water" with κ = 0.043 × 10–6 S cm–1 at 18°C. Ordinary distilled water in equilibrium with atmospheric CO2 has a conductivity that is 16 times greater.

It is now known that ordinary distillation cannot entirely remove all impurities from water. Ionic impurities get entrained into the fog created by breaking bubbles and are carried over into the distillate by capillary flow along the walls of the apparatus. Organic materials tend to be steam-volatile ("steam-distilled").
The best current practice is to employ a special still made of fused silica in which the water is volatilized from its surface without boiling. Complete removal of organic materials is accomplished by passing the water vapor through a column packed with platinum gauze heated to around 800°C through which pure oxygen gas is passed to ensure complete oxidation of carbon compounds.
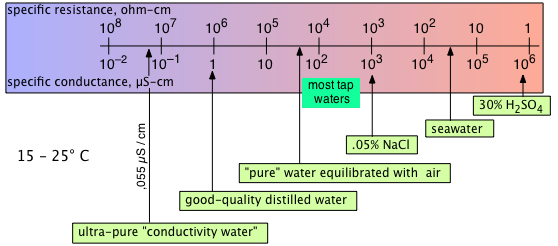
Conductance measurements are widely used to gauge water quality, especially in industrial settings in which concentrations of dissolved solids must be monitored in order to schedule maintenance of boilers and cooling towers.
The conductance of a solution depends on 1) the concentration of the ions it contains, 2) on the number of charges carried by each ion, and 3) on the mobilities of these ions. The latter term refers to the ability of the ion to make its way through the solution, either by ordinary thermal diffusion or in response to an electric potential gradient.
The first step in comparing the conductances of different solutes is to reduce them to a common concentration. For this, we define the conductance per unit concentration which is known as the molar conductivity, denoted by the upper-case Greek lambda:
\[Λ = \dfrac{κ}{c}\]
When κ is expressed in S cm–1, C should be in mol cm–3, so Λ will have the units S cm2. This is best visualized as the conductance of a cell having 1-cm2 electrodes spaced 1 cm apart — that is, of a 1 cm cube of solution. But because chemists generally prefer to express concentrations in mol L–1 or mol dm–3 (mol/1000 cm3) , it is common to write the expression for molar conductivity as
\[Λ = \dfrac{1000κ}{c}\]
electrodes, separated again by 1 cm.But if c is the concentration in moles per liter, this will still not fairly compare two salts having different stoichiometries, such as AgNO3 and FeCl3, for example. If we assume that both salts dissociate completely in solution, each mole of AgNO3 yields two moles of charges, while FeCl3 releases six (i.e., one Fe3+ ion, and three Cl– ions.) So if one neglects the [rather small] differences in the ionic mobilities, the molar conductivity of FeCl3 would be three times that of AgNO3.
The most obvious way of getting around this is to note that one mole of a 1:1 salt such as AgNO3 is "equivalent" (in this sense) to 1/3 of a mole of FeCl3, and of ½ a mole of MgBr2. To find the number of equivalents that correspond a given quantity of a salt, just divide the number of moles by the total number of positive charges in the formula unit. (If you like, you can divide by the number of negative charges instead; because these substances are electrically neutral, the numbers will be identical.)
We can refer to equivalent concentrations of individual ions as well as of neutral salts. Also, since acids can be regarded as salts of H+, we can apply the concept to them; thus a 1M L–1 solution of sulfuric acid H2SO4 has a concentration of 2 eq L–1.
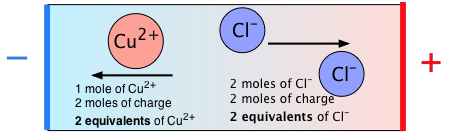
The following diagram summarizes the relation between moles and equivalents for CuCl2:
What is the concentration, in equivalents per liter, of a solution made by dissolving 4.2 g of chromium(III) sulfate pentahydrate Cr2(SO4)3·5H2O in sufficient water to give a total volume of 500 mL? (The molar mass of the hydrate is 482 g)
Solution
Assume that the salt dissociates into 6 positive charges and 6 negative charges.
- Number of moles of the salt: (4.2 g) / (482 g mol–1) = 0.00871 mol
- Number of equivalents: (.00871 mol) / (6 eq mol–1) = 0.00146 eq
- Equivalent concentration: (0.00146 eq) / (0.5 L) = 0.00290 eq L–1
The concept of equivalent concentration allows us to compare the conductances of different salts in a meaningful way. Equivalent conductivity is defined similarly to molar conductivity
\[Λ = \dfrac{κ}{c}\]
except that the concentration term is now expressed in equivalents per liter instead of moles per liter. (In other words, the equivalent conductivity of an electrolyte is the conductance per equivalent per liter.)


