8.10.9E: Some applications of electrolytic conduction
- Page ID
- 20113
From the chemist's standpoint, the most important examples of conduction are in connection with electrochemical cells, electrolysis and batteries.
Determination of equilibrium constants
Owing to their high sensitivity, conductivity measurements are well adapted to the measurement of equilibrium constants for processes that involve very small ion concentrations. These include
- Ks values for sparingly soluble solids
- Autoprotolysis constants for solvents (such as Kw )
- Acid dissociation constants for weak acids
As long as the ion concentrations are so low, their values can be taken as activities, and limiting equivalent conductivities Λ0 can be used directly.
Ion product of water
The very small conductivity of pure water makes it rather difficult to obtain a precise value for Kw; better values are obtained by measuring the potential of an appropriate galvanic cell. But the principle illustrated here might be applicable to other autoprotolytic solvents such as H2SO4.
Use the appropriate limiting molar ionic conductivities to estimate the autoprotolysis constant Kw of water at 25° C. Use the reaction equation
2 H2O → H3O+ + OH–.
Solution: The data we need are λH+ = 349.6 and λOH– = 199.1 S cm2 mol–1.
The conductivity of water is κ = [H+] λH+ + [OH–] λOH– whose units work out to (mol cm–3) (S cm2 mol–1). In order to express the ionic concentrations in molarities, we multiply the cm–3 term by (1 L / 1000 cm–3), yielding
1000 κ = [H+] λH+ + [OH–] λOH– with units S cm–1 L–1.
Recalling that in pure water, [H+] = [OH–] = Kw½, we obtain
1000 κ = (Kw½)(λH+ + λOH– ) = (Kw½)(548.7 S cm2 mol–1).
Solving for Kw:
Kw = (1000 κ / 548.7 S cm2 mol–1)2
Substituting Kohlrausch's water conductivity value of 0.043 × 10–6 S cm–1) for κ gives
Kw =(1000 × 0.043 × 10–6 S cm–1 / 548.7 S cm2 mol–1)2 = 0.614 × 10–14 mol2 cm–6 (i.e., mol2 L–2).
The accepted value for the autoprotolysis constant of water at 25° C is Kw = 1.008 × 10–14 mol2 L–2.
A saturated solution of silver chloride AgCl has a conductance 2.28 x 10–6 S cm–1 at 25°C. The conductance of the water used to make up this solution is 0.116 x 10–6 S cm–1. The limiting ionic conductivities of the two ions are λAg+= 61.9 and λCl– = 76.3 S cm2 mol–1. Use this information to estimate the molar solubility of AgCl.
The limiting molar conductivity of the solution is
Λo = λAg+ + λCl– = 138.2 S cm–1.
The conductance due to the dissociated salt alone is the difference
(2.785 – 0.043) = 2.16 x 10–6 S cm–1.
Substituting into the expression Λ = 1000κ/c yields
= 1.56 x 10–5 mol/1000 cm3or 1.56 x 10–5 mol L–1.Conductometric titration
A chemical reaction in which there is a significant change in the number or mobilities of ionic species can be followed by monitoring the change in conductance. Many acid-base reactions fall into this category. In conductometric titration, conductometry is employed to detect the end-point of a titration.

Consider, for example, the titration of the strong acid HCl by the strong base NaOH. In ionic terms, the process can be represented as
H+ + Cl– + Na+ + OH– → H2O + Na++ Cl–
At the end point, only two ionic species remain, compared to the four during the initial stages of the titration, so the conductivity will be at a minimum. Beyond the end point, continued addition of base causes the conductivity to rise again. The very large mobilities of the H+and OH– ions cause the conductivity to rise very sharply on either side of the end point, making it quite easy to locate.
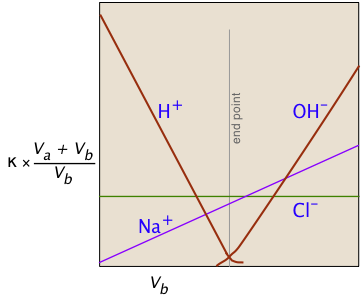

The plot on the left depicts the conductivities due to the individual ionic species. But of course the conductivity we measure is just the sum of all of these (Kohlrausch's law of independent migration), so the plot on the right corresponds to what you actually see when the titration is carried out. The factor (Va + Vb)/Vb compensates for the dilution of the solution as more base is added.
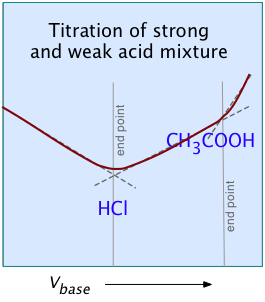

For most ordinary acid-base titrations, conductometry rarely offers any special advantage over regular volumetric analysis or potentiometry. But in some special cases such as those illustrated here, it is the only method capable of yielding useful results.
Ground- and soil conduction
Most people think of electrolytic conduction as something that takes place mainly in batteries, electrochemical plants and in laboratories, but by far the biggest and most important electrolytic system is the earth itself, or at least the thin veneer of soil sediments that coat much of its surface.
Soils are composed of sand and humic solids within which are embedded pore spaces containing gases (air and microbial respiration products) and water. This water, both that which fills the pores as well as that which is adsorbed to soil solids, contains numerous dissolved ions on which soil conductivity mainly depends. These ions include exchangeable cations present on the surfaces of the clay components of soils. Although these electrolyte channels are small and tortuously connected, they are present in huge numbers and offer an abundance of parallel conduction paths, so the ground itself acts as a surprisingly efficient conductor.
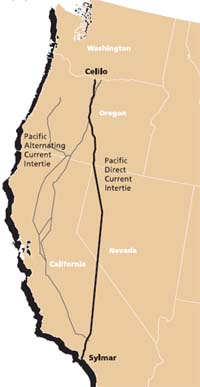
There is no better illustration of this than the use of a ground path to transmit a current of up to 1800 amperes along the 1360-km path of the Pacific DC Intertie that extends from the Celilo Converter Station (view below) in northern Oregon to Los Angeles. This system normally employs a two-conductor power line that operates at ±500,000 volts DC, but when one of these conductors is out of service, the ground path acts as a substitute conductor. This alternative path is said to have a lower resistance than the normal metallic conductor!
From an electrochemical standpoint, the most interesting aspect of this system is the manner in which the current flows into or out of the ground. The grounding system at Celilo is composed of over 1000 cast-iron electrodes buried in a circular 3.3-km trench of petroleum coke which acts as the working electrode. At the Los Angeles end, grounding is achieved by means of 24 silicon-iron alloy electrodes submerged in the nearby Pacific Ocean.
On a much smaller scale, single-wire earth return systems are often employed to supply regular single-phase ac power to remote regions, or as the return path for high-voltage DC submarine cables. For direct current submarine systems, a copper cable laid on the bottom is suitable for the cathode. The anodes are normally graphite rods surrounded by coke.
You may have noticed that the pole-mounted step-down transformers used to distribute single-phase ac power in residential neighborhoods are connected to the high-voltage (10 Kv or so) primary line by only a single wire. The return circuit back to the local substation is completed by a ground connection which runs down the pole to a buried electrode.

The Celilo Converter Station is located at The Dalles, Oregon
Other applications of ground conductivity
- Ground-wave radio propagation
- During the daytime, radio transmission at frequencies below about 5 Mhz (such as in the old standard AM broadcast band) depends entirely on so-called ground waves that follow the curvature of the earth. This occurs because that portion of the vertically-polarized wavefronts in contact with the earth induce an electrolytic current in the ground, causing their lower portions to travel more slowly, bending their pathways in toward the earth.
- Agricultural and environmental soils assessment
- Conductivity has long been used as a tool to assess the salinity of agricultural soils — a serious problem in irrigated regions, where evaporation of irrigation water over the years can raise salinity to levels that can reduce crop yields. Because other soil characteristics (moisture content, density, and mineralogy, fertilization) also play important roles, some care is required to correctly interpret measurements. Measuring devices that can be drawn behind a tractor and are equipped with GPS receivers allow the production of conductivity maps for entire fields.
- Archaeological exploration
- Buried artifacts such as stone walls and foundations and large metallic objects can be located by a series of conductivity measurements at archaeological sites.